벡터란 무엇인가?

벡터의 기본 연산에 대해 이야기 하기 전에 벡터란 무엇인지부터 생각해보도록 하자.

1) 벡터란 화살표 같은 것

우선 바로 떠오르는 것은 벡터란 물리학에서 말하는 ‘크기와 방향으로 정의되는 값’이라고 할 수 있다.

이것은 기하학적인 벡터의 특성을 잘 반영하고 있는 정의라고 할 수 있으며, 특히 벡터의 좌표계의 변환에 대한 불변성(invariance)을 잘 표현하고 있다.

좌표계의 변환에 대해 불변적이라는 말은 아래 그림에서 처럼 좌표계가 변하더라도 벡터 그 자체는 가만히 있다는 것을 의미한다.

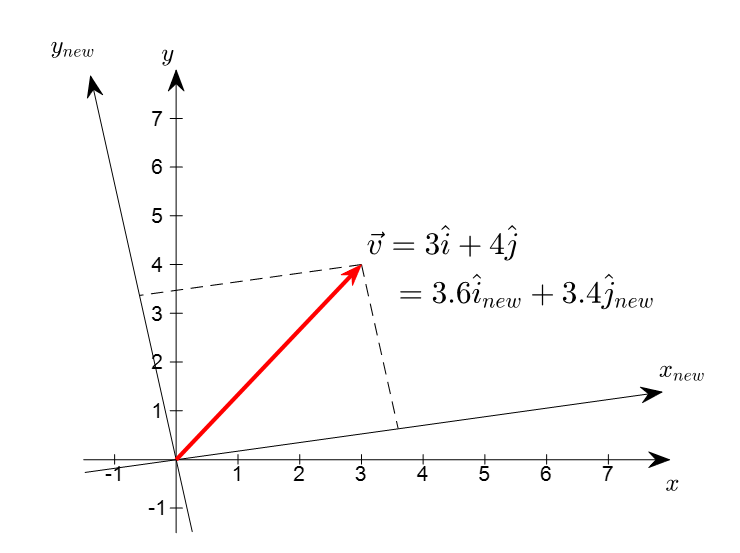
그림 1. 좌표계의 변환과 벡터. 좌표계가 변할 때 벡터는 변하지 않지만 벡터의 성분은 변한다.

이러한 벡터 정의에 대해 첨언하자면 이러한 ‘크기와 방향으로 정의되는 값’이라는 설명은 Euclidean 벡터에 한해서만 적용해 설명할 수 있다는게 한계점이다.

하지만, 이러한 정의는 벡터를 시각화하는데 매우 유용하므로 특별한 언급이 없는 이상 Euclidean 벡터를 이용해 시각화 할 것이다.

2) 벡터란 숫자를 순서대로 나열한 것

또, 벡터에 대해 생각해볼 수 있는 정의는 순서를 맞춰 숫자를 나열한 리스트라는 관점이다.

이 관점은 벡터는 하나의 데이터 포인트라는 관점에서 매우 유용하다.

또한, 이런 방식으로 벡터를 생각하게 되면 차원을 무한히 늘리는데에 큰 부담이 없다. 그저 숫자만 더 나열하면 더 고차원의 벡터가 되기 때문이다.

그리고 벡터 성분이 좌표계의 변환에 대해 가변적(not invariant)이라는 점을 잘 표현해주고 있다.

가변적이라는 말을 좀 더 잘 이해하기 위해 그림 1을 다시 보자.

그림 1에서는 벡터를 두 가지 좌표계로 표현하고 있는데, 벡터는 가만히 있더라도 벡터를 보는 좌표계가 바뀌게 되면 벡터를 표현하는 좌표가 바뀌는것을 볼 수 있다.

3) 벡터란 벡터 공간의 원소

위의 두 정의를 차처하고, 수학적으로 가장 의미있는 정의는 벡터란 그저 벡터 공간(vector space)의 원소라고 말하는 것이다.

이건 마치 대학생은 ‘대학교에 다니는 사람’으로 정의하는 것 마냥 대학교에 대해 잘 알고있는 사람이라면 한번에 이해할 수 있지만, 그렇지 않다면 결국 다시 맴도는 정의처럼 보인다.

이런 방식으로 벡터를 정의하는 것은 이러한 특성을 가진 것들은 모두 벡터로 취급해서 다룰 수 있다는 점을 강조한 것이다.

가령, 함수나 행렬같은 얼핏 보기에는 우리가 평소 알고있는 벡터가 아닌 개념들도 벡터에 적용할 수 있는 여러가지 기법들을 적용해 응용할 수 있다는 점을 부각시킨다고 할 수 있다.

벡터 공간에 대해서는 차후에 좀 더 다루겠지만, 벡터 공간은 다음과 같은 세 가지 요소가 정의되고 성립되어야 한다.

\[(V, +, \cdot)\]

여기서 $V$는 벡터, $+$는 덧셈 규칙, $\cdot$은 곱셈 규칙을 의미한다¹.

지금으로썬 너무나 모호하게 들리는 추상적인 정의이지만, 이러한 추상성이 벡터의 개념을 더 넓은 범위로 확장하고 이를 이용해 선형대수학의 세계에서 일어나는 많은 일들을 설명할 수 있게 된다.

벡터의 기본 연산

사실 벡터의 기본 연산은 정말 단순하다.

벡터의 기본 연산은 총 두 가지 이며 각각이 상수배, 그리고 벡터 간의 합이다.

벡터의 상수배(scalar multipliation)

임의의 집합 $V(\neq \phi)$에 대해 임의의 벡터 $x\in V$와 스칼라 $k\in {\Bbb R}$에 대하여 다음이 성립하여야 한다.

\[x\in V, k\in {\Bbb R} \Rightarrow kx\in V\]

그림으로 설명하자면, 주어진 화살표에 대해서 화살표의 크기가 늘어나거나 줄어드는 것을 의미할 수 있다.

그림 2. 다양한 스칼라값에 대응하여 크기가 커지거나 작아지는 2차원 실수 공간 상의 벡터

벡터 간의 합

임의의 집합 $V(\neq \phi)$에 대해 임의의 벡터 $x, y\in V$에 대하여 다음이 성립하여야 한다.

\[x, y\in V, \Rightarrow x+y\in V\]

그림으로 설명하자면 주어진 두 화살표에 대해 화살표의 크기와 방향을 합해주어 평행사변형 꼴을 이룰 수 있도록 합해진 벡터가 출력되면 된다.

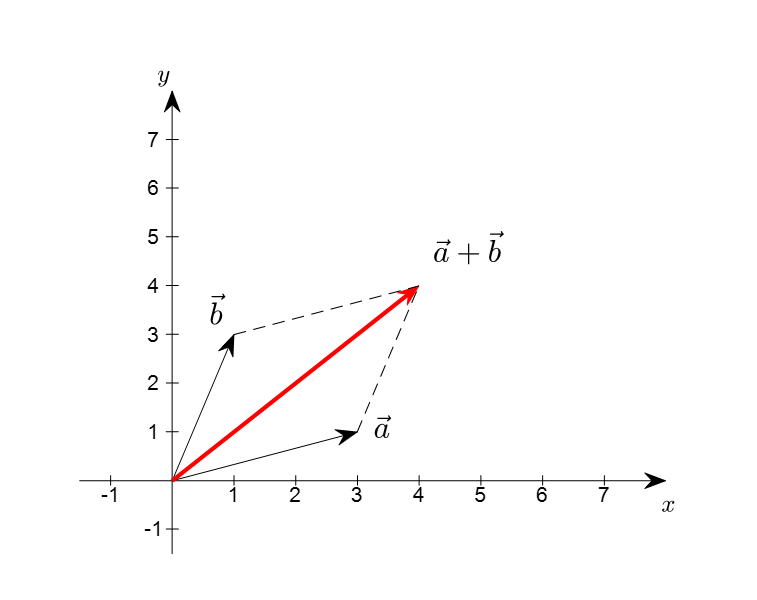
그림 3. 두 벡터 $\vec{a}$와 $\vec{b}$의 합인 $\vec{a}+\vec{b}$

약간의 부연설명을 하자면, 물리학에서 말하는 벡터와 수학에서 말하는 벡터는 약간 차이가 있는데, 수학에서는 모든 벡터들의 시점이 원점이어야 한다.

상수배와 벡터 간의 합이 중요한 이유

기본적으로 상수배와 벡터 간의 합이 중요한 것은 이 두 연산이 잘 정의되는 것(entity)들은 선형성을 만족한다고 할 수 있기 때문이다.

선형성에 대해서는 차츰 더 다루겠지만, 쉽게 말하자면 선형성을 만족하는 개념들은 수학적으로 다루기가 쉽기 때문에 선형성을 만족하는 것들을 찾고 연구한다고 생각하자.

앞으로 다루게 될 개념들 중 상수배와 벡터 간의 합이 기초가 되는 개념들을 살펴보자면 다음을 생각해볼 수 있을 것이다.

가장 기초적인 데이터 변형 방법

위의 벡터에 대한 관점 중 두 번째 관점인 ‘벡터는 숫자들을 순서대로 나열한 것’이라는 관점에서 상수배와 벡터간의 합이 중요할 수 있다.

즉, 데이터를 벡터로 생각하여 데이터를 처리한다고 보는 관점의 응용이다.

가령 5명 사람의 국어 성적과 영어 성적의 평균 점수를 계산한다고 해보자.

국어 성적에 대한 정보를 벡터로 표현하면 다음과 같을 수 있다.

\[k = \begin{bmatrix}100\\70\\30\\45\\80\end{bmatrix}\]

또 만약 영어 점수에 대한 정보를 벡터로 표현하면 다음과 같을 수 있다.

\[e = \begin{bmatrix}83\\50\\25\\30\\60\end{bmatrix}\]

이 때, 두 점수의 평균 점수를 매기는 방법은 아래와 같을 것이다.

\[avg = \frac{1}{2}k + \frac{1}{2}e = \frac{1}{2}\begin{bmatrix}100\\70\\30\\45\\80\end{bmatrix}+\frac{1}{2}\begin{bmatrix}83\\50\\25\\30\\60\end{bmatrix}\]

지금은 단순한 평균에 대한 예시를 작성하였지만 추후에 배울 여러가지 데이터 처리 기법들(PCA, SVD, 선형 회귀, 독립성분분석 …)등의 수많은 기법들이 위와 같이 데이터를 벡터로 생각하여 데이터가 처리된다는 점을 강조하고 싶다.

벡터 간의 선형 결합

좀 더 근본적으로는 벡터 간의 선형 결합(linear combination)을 표현하기 위해 상수배와 벡터 간의 합은 필수적인 개념이다.

상수배와 벡터간의 합을 한번에 활용하면 다음 예시에서와 같이 두 개의 임의의 벡터에 대한 선형결합을 표현할 수 있다.

\[\Rightarrow c_1\begin{bmatrix}1\\0 \end{bmatrix}+c_2\begin{bmatrix}0\\1 \end{bmatrix}\]

선형 결합이라는게 단어가 어려워서 그렇지 사실은 상수배와 벡터간의 합을 한번에 조합해 표현한 것이다.

그러면 이 단순한 상수배와 벡터간의 합인 선형 결합이 뭐가 그렇게 중요한걸까?

위의 예시에서 $c_1$, $c_2$은 각각이 모든 실수에 대응될 수 있는데, $c_1$, $c_2$가 바뀌면서 얻게되는 선형결합의 결과는 2차원 실수 벡터 공간 상에 있는 모든 벡터들에 대응되게 된다.

그림 4. 다양한 $c_1$과 $c_2$에 대해 대응하는 2차원 실수 공간 상의 벡터

이러한 벡터 간의 선형 결합이 어떤 벡터공간 전체에 대응된다는 개념을 공간 생성(span)이라고 하며, 이는 행렬 곱과 연립방정식의 해를 얻는 과정에 대한 새로운 관점을 제시해줄 아주 중요한 단서가 된다.