※ 이 포스팅은 미술관에 GAN 딥러닝 실전 프로젝트의 결과와 소스 코드를 이용해 작성한 것임을 밝힙니다.
※ 이 포스팅의 소스 코드는 박해선 님의 깃허브 레포에서 확인하실 수 있습니다.
이번 시간에는 RBM과 함께 딥러닝 이론 구축의 근간이 되었던 개념 중 하나인 AutoEncoder(이하 AE)에 대해 알아보고자 한다.
Restricted Boltzmann Machine(이하 RBM)과 AE는 거의 유사한 목표를 갖고 있다. 둘의 목표는 모두 hidden layer에서 input layer(혹은 visible layer)의 데이터에 관한 latent factor들을 얻어내는 것이다.
이 말이 조금 어렵게 들릴 수 있는데, 조금 쉽게 설명하자면 AE는 데이터를 압축하고, 다시 압축 해제하는 과정을 거치게 만든 뉴럴네트워크이다.
그럼 굳이 압축 해제해서 원래 데이터를 얻을 것을 왜 굳이 압축을 할까?
첫번째로는 이 뉴럴넷이 압축하는 방식을 배웠으면 하기 때문이다. 다시 말해, 비선형적인 차원감소를 수행하고, 이를 통해 원래 고차원의 데이터를 더 낮은 차원에서 표현하고 싶기 때문이다.
아마 이 과정에서 일부 데이터의 손실이 발생할 수 있는데, 이 손실을 최소화 해주기 위한 프로세스를 통해 더 좋은 AE로 훈련받을 수 있는 것이다.
두 번째로는 지금껏 전혀 보지 못한 데이터를 생성할 때에 AE가 힘을 발휘할 수 있기 때문이다.
앞서 언급한 압축의 첫 번째 이유에서 더 낮은 차원의 압축된 데이터를 얻는다고 말했다. 이것을 거꾸로 생각해 보자.
이미 잘 훈련된 AE가 있다고 하면, 압축된 낮은 차원의 벡터 공간에서 임의의 점을 선정해 다시 압축해제를 시키면 지금껏 보지 못한 데이터가 생성될 수 있다.
왜냐면 AE는 낮은 차원에 표현되어 있는 데이터를 다시 높은 차원으로 압축 해제하는 방법을 잘 배웠을 것이기 때문이다.
이러한 두 가지 이유에 해당하는 일을 수행하는 것을 인코딩과 디코딩이라고 말한다. 즉, 압축 과정을 인코딩, 압축 해제 과정을 디코딩이라고 부른다. 그리고 이러한 일들을 수행하는 파트들을 각각 인코더, 디코더라고 부른다.
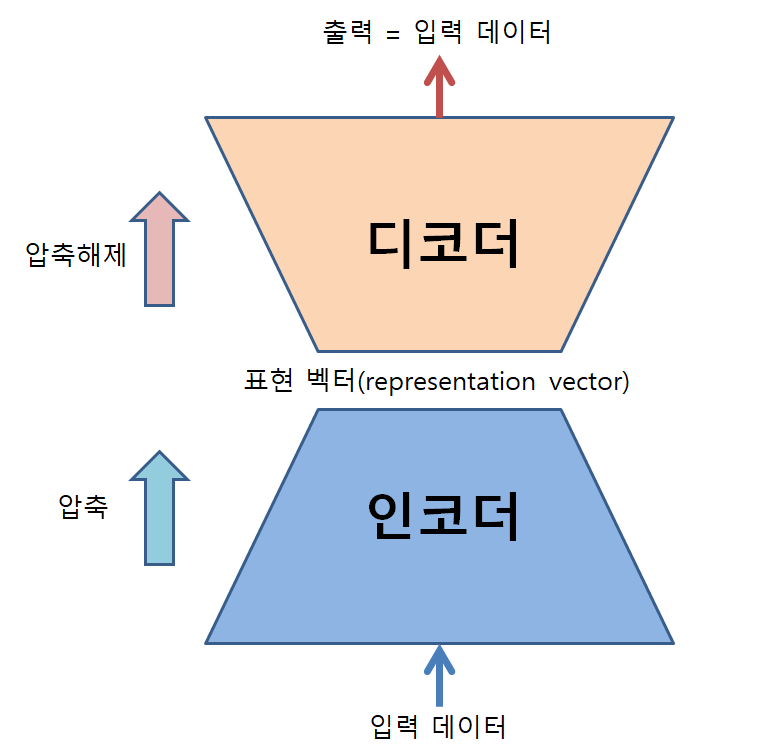
그림 1. 오토인코더의 구조와 역할
압축의 관점에서: 인코더의 역할
데이터를 압축한다는 것은 다른 말로하면 “차원감소”와 비슷한 말로 볼 수 있다.
하지만, 차원감소라는 말 대신 “압축”이라는 말을 굳이 사용하고 있는 것은 선형적인 차원감소에서 사용하는 “투영(혹은 정사영)”이 아닌 비선형적인 방식의 차원 감소가 이루어지기 때문이다.
오토인코더(AutoEncoder, AE)로 데이터를 압축하면 우리는 그 결과로써 표현 벡터(representation vector)를 얻을 수 있다.
이 표현 벡터를 직관적으로 잘 이해할 수 있는 방법 중 하나는 표현 벡터를 2차원 혹은 3차원 벡터로 받아 이 것을 직접 그려보는 것이다.
이번 posting에서는 MNIST 데이터를 AE에 적용해 차원 압축을 시켜보고자 한다.
MNIST 데이터에 대해 짧게 설명하자면 아래의 그림과 같이 0에서 9까지의 숫자를 손으로 쓴 그림들을 포함하고 있는 데이터셋이다.
각 그림은 28x28 픽셀의 크기로 구성되어 있다.

그림 2. MNIST 데이터셋의 일부 샘플
그림 출처: Wikipedia MNIST 데이터베이스
아래는 MNIST 데이터를 이용해 784 차원의 데이터 (28 x 28)를 2차원으로 압축해 얻은 표현 벡터를 label 별로 색깔을 달리하여 표시한 것이다.
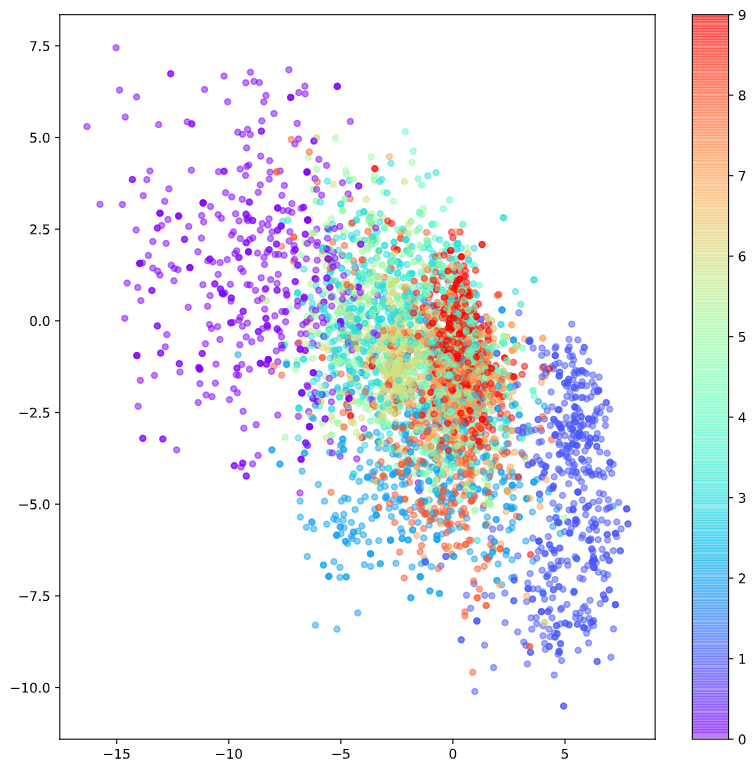
그림 3. MNIST 데이터의 representation vector의 시각화
그림 2를 보면 알 수 있는 것은 0으로 labeling이 된 데이터들(보라색)은 좌측 상단에 퍼져있듯이 위치하고 있는데, 다른 label의 숫자들과는 떨여져 있다는 것이다.
또, 1로 labeling된 데이터들은 우측 하단에 퍼져있고, 다른 label의 숫자들과 떨어져 있다.
반면 0과 1의 label이 아닌 데이터들은 중앙에 함께 퍼져서 위치하는 것을 알 수 있다.
우선은 각 label별로 분리되지 않고 뭉쳐져서 representation vector가 표시되고 있는 것에 대해서는 크게 신경쓰지 말도록 하자. 이 결과에 대한 더 좋은 성능을 얻는 방법은 Variational AutoEncoder 편에서 추가로 다루도록 하겠다.
어찌되었건 AE에서 인코더의 역할은 주어진 고차원의 데이터(여기선 784차원의 데이터)를 낮은 차원의 벡터(여기선 2차원)으로 압축시켜 표현할 수 있게 해준다는 것이다.
참고로 새로운 용어를 하나 더 언급하자면, 표현 벡터(representation vector)가 표시되어 있는 벡터 공간을 조금 어려운 말로 잠재 공간(latent space)이라고 부른다.
압축 해제의 관점에서: 디코더의 역할
이번엔 AE를 디코더 관점에서 생각해보도록 하자.
디코더는 잠재 공간(latent space)안에 있는 임의의 representation vector를 주어주었을 때, 그것이 갖고 있는 원래의 의미를 “압축 해제”하여 원본 사이즈의 데이터 형태로 복원시키는 역할을 한다.
아래의 그림 3에서는 MNIST 데이터셋이 표현된 2차원 잠재 공간에서 임의의 representation vector를 샘플링하는 모습을 확인할 수 있다.
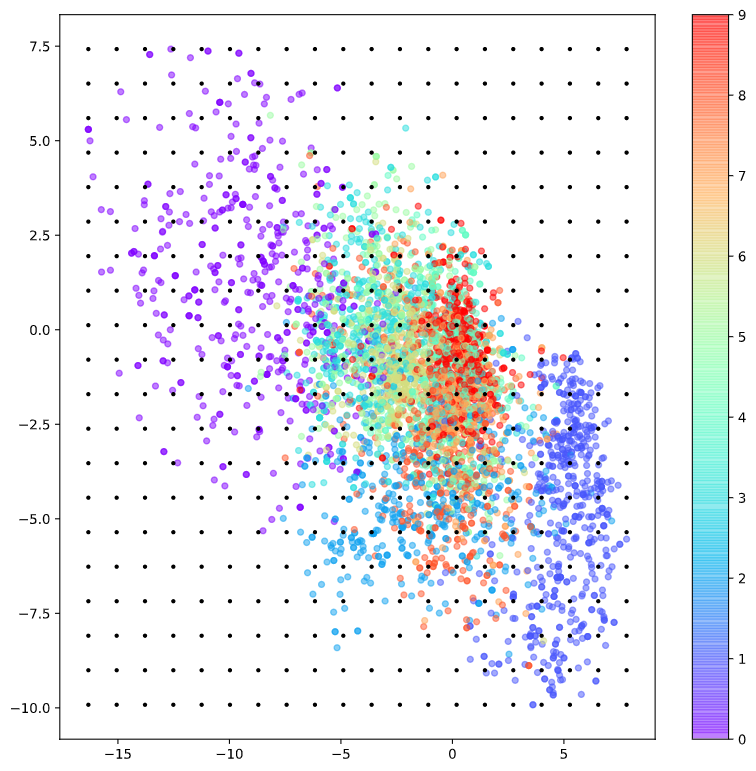
그림 4. MNIST 데이터의 2차원 잠재 공간에서 임의의 representation vector를 샘플링(검은색 점)
이 때, 샘플링 된 점들에 대한 “압축 해제” 결과는 아래의 그림 4와 같다.

그림 5. 임의의 representation vector들을 디코딩("압축 해제")한 결과
그림 3에서 0과 1이 다른 label들의 숫자 데이터에서 뚜렷히 구분되어 떨어져 있는 것이 그림 4의 디코딩 결과에서도 일맥상통하게 확인되는 것을 알 수 있다.
다시 말하면, 그림 4에서 0과 1은 가장 뚜렷하게 다른 숫자들과 구별되는 것을 알 수 있다.
반면에 다른 숫자들은 어느정도 그 숫자의 형태가 뚜렷이 구분되는 것도 있는가하면 전혀 숫자처럼 보이지 않는 새로운 형태의 데이터들도 확인해볼 수 있다.
또 한가지 재밌는 점은 그림 4의 가장 아래의 행을 보면 0, 2, 8, 1의 순서대로 그림의 형태가 부드럽게 transition 되는 것 또한 확인해볼 수 있다.
AE의 입출력 결과
그렇다면 원래 AE의 역할인 ‘원래의 입력을 출력으로 내주는 것’의 기능은 충실히 다 할 수 있었을까?
썩 만족할만한 성능은 아니지만, 어느정도는 원래의 이미지를 복원해주고 있다는 것을 알 수 있다.

그림 6. 입력을 재구성한 그림 예시
AE와 딥러닝의 관계?
딥러닝의 핵심적인 내용은 단순히 “뉴럴네트워크의 층이 깊다”정도에서 끝나는 것이 아니라, “층이 깊어질 때 어떤 좋은 효과가 있는가”에 있다.
알려진 바에 따르면 뉴럴네트워크는 훈련이 잘 되었다고 가정했을 때, input에 가까운 layer에서는 단순한 pattern에 대한 feature를 추출하는 반면 층이 input에서 멀어질 수록(즉, 깊어질 수록) 더 추상적인 개념에 대해 학습하고 추상적인 feature를 추출할 수 있게 된다고 알려져 있다.
이 때, AE는 input dataset의 representation vector를 얻는데, 이것을 관점을 바꿔 생각하면 데이터에 대한 추상화를 실시하고 있는 것이다. 데이터가 갖는 특성들을 작은 공간안에 우겨넣으려다보니 상징적인 특성들로 구성된 latent space를 생성해야 하는 것이다.
이렇듯 AE를 이용해 더 깊은 층을 쌓는 것을 Stacked AutoEncoder라고 하며, 이렇게 얻어낸 입력 데이터의 추상적인 특성들을 fine-tuning하면 깊은 뉴럴네트워크를 훈련시킬 수 있을 것이라는 생각이 지금의 딥러닝 알고리즘을 있게한 것이라고 할 수 있다.
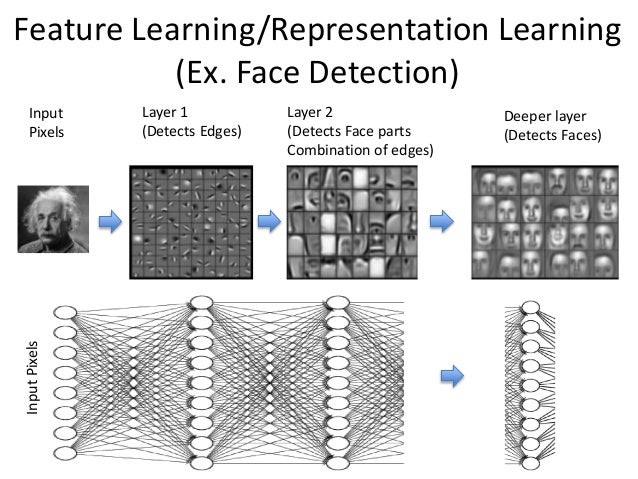
그림 6. 딥-뉴럴네트워크는 더 깊은 층에서 더 추상적인 feature를 추출할 수 있도록 학습된다.
그림 출처