Prerequisites
경계값 문제에 대한 포스팅을 잘 이해하기 위해서는 다음의 내용에 대해 알고 오시는 것이 좋습니다.
경계값 문제란?
지금까지 미분방정식의 해를 구할 때 우리는 초기값 문제를 가지고 해를 구했다. 초기값 문제는 쉽게 말해 어디서부터 미분방정식의 해(solution)의 성장을 진행시킬까에 관한 문제였다.
즉, 식으로 쓰자면 다음과 같은 조건이 주어진 경우에 문제를 풀 수 있는 것이다. 풀고자하는 미분방정식이 2계 미분방정식이라고 하면 초기 조건은 다음과 같은 것이다.
\[x(t_0) = x_0, \quad x'(t_0)=x_0' % 식 (1)\]즉, 독립변수가 시간이라고 생각하고 $x(t)$가 위치에 관한 함수라고 하면 초기 위치와 초기 속도에 대한 값만을 가지고 이후의 궤적이 어떻게 될지를 생각해보는 문제라고 할 수 있다.
하지만, 어떤 경우에는 시작 시점과 종료 시점의 함수값 혹은 미분계수의 값이 주어지는 문제도 있을 수 있다.
가령, 로켓을 발사했을 때 처음 위치와 시점을 가지고 이후의 궤적을 구하는 것이 아니라 처음 발사 시점의 위치와 도달 위치를 정확하게 알고 있는 경우의 중간 과정이 어떻게 되어야 할지를 푸는 문제에서는 시작 시점과 종료 시점의 함수값이 주어져야 한다.
이런 문제를 경계값 문제라고 하며 경계값 문제에 해당하는 조건은 다음과 같은 네 가지 경우 중 하나이다.
\[x(t_0) = x_0, \quad x(t_1) = x_1 % 식 (2)\] \[x'(t_0) = x'_0, \quad x'(t_1) = x'_1 % 식 (3)\] \[x'(t_0) = x'_0, \quad x(t_1) = x_1 % 식 (4)\] \[x(t_0) = x_0, \quad x'(t_1) = x'_1 % 식 (5)\]즉, 시작 시점($t_0$)과 종료 시점($t_1$)에서의 함수값 혹은 미분계수의 값이 조건으로 주어진 것이며 이 조건을 우리는 경계 조건(boundary condition)이라고 한다.
경계값 문제는 초기값 문제보다 더 풀기가 어렵고, 이에 관한 내용은 매우 방대하다.
그러나 지금 우리는 경계값 문제가 초기값 문제와 어떻게 다른지에 대해 간단히 시각적으로 확인해보고자 한다.
시각적 설명
초기값 문제와 경계값 문제의 시각적 비교
아래와 같은 2계 선형미분방정식을 생각해보자.
\[\frac{d^2x}{dt^2}-4\frac{dx}{dt}+3x(t) = 0 % 식 (6)\]이 미분방정식은 2계 선형미분방정식의 해법 편에서 보았던 것 처럼 아래와 같은 연립 미분방정식으로 바꿔 풀수 있다.
\[\Rightarrow \begin{bmatrix}dx/dt \\ dy/dt\end{bmatrix} = \begin{bmatrix}0 & 1 \\ -3 & 4\end{bmatrix}\begin{bmatrix}x \\ y\end{bmatrix} % 식 (7)\]만약 여기서 아래와 같은 두 가지 경우를 생각해보자. 하나는 초기 조건이 주어진 경우이고 또 다른 하나는 경계 조건이 주어진 경우이다.
\[\text{1) 초기 조건: }x(0) = 2,\quad x'(0) = 2 % 식 (8)\] \[\text{2) 경계 조건: }x(1) = 2,\quad x(3) = 7 % 식 (9)\]그림으로 그리자면 식 (7)을 가지고 표현할 수 있는 방향장에 대해 식 (8)과 식 (9)는 아래의 그림 1과 같은 세팅을 하게 되는 것이다.
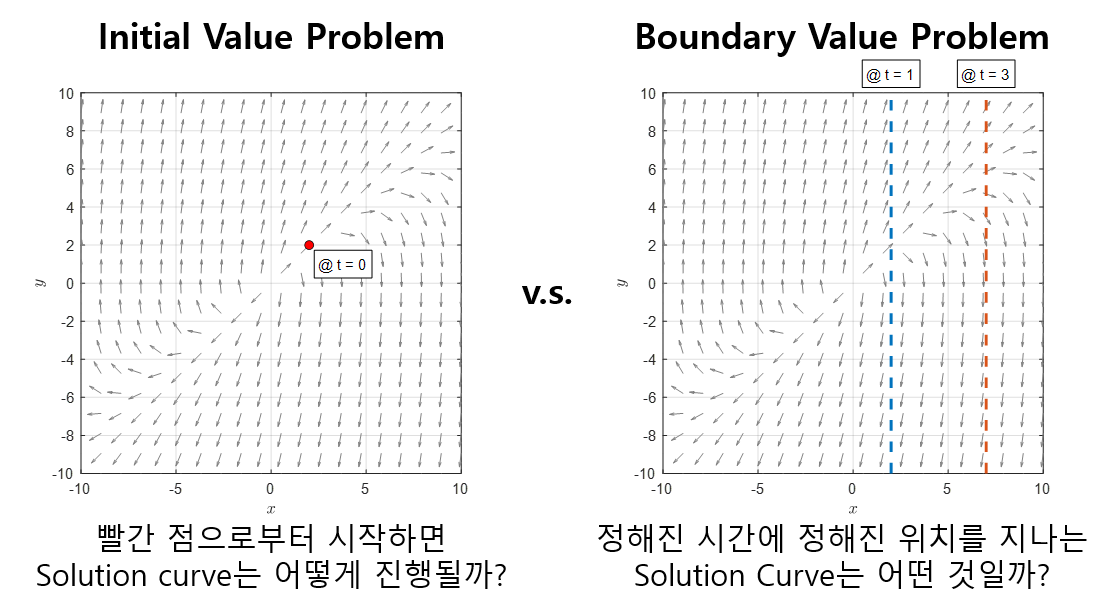
그림 1. 초기값 문제와 경계값 문제의 비교
생각해보면 초기값 문제는 시작점으로부터 주어진 방향을 따라 solution curve를 그려나가면 되지만, 경계값 문제는 정해진 시점에 맞춰진 함수값을 갖는 정확한 함수를 알아내야 하므로 초기값 문제보다 경계값 문제가 더 어렵게 보인다.
초기값 문제에 대한 solution curve들은 많이 구해봤으니 식 (9)로 주어진 경계값 문제에 대한 solution curve를 그려보면 아래의 그림과 같이 구할 수 있다 (MATLAB의 bvp4c solver를 이용해 plot).
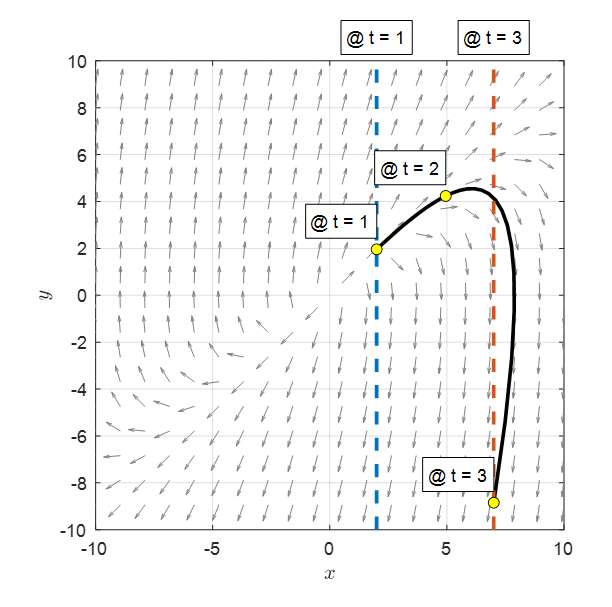
그림 2. 주어진 경계값 문제에 대한 solution curve
경계값 문제의 해 유도(analytic solution)
해석적으로 미분방정식의 해를 구해내는 관점에서 보면 경계값 문제든 초기값 문제든 별반 다를게 없어 보이긴 한다.
아래와 같이 얻어진 일반해에 대해서,
\[\begin{bmatrix}x(t) \\ y(t) \end{bmatrix} = c_1 \begin{bmatrix}1 \\3 \end{bmatrix}e^{3t}+c_2\begin{bmatrix}1 \\ 1\end{bmatrix}e^t\]경계값 조건을 대입하면 아래와 같은 식을 얻을 수 있다.
경계값 조건은 $x(t)$에 해당되는 값들만 주어진 것이므로 위 식에서 1행에 해당되는 값에 대해서만 조건을 적용하면,
\[\text{at }t=1\text{, }x(1)=c_1e^3 + c_2 e=2\] \[\text{at }t=3\text{, }x(3)=c_1e^{3\cdot 3} + c_2 e^3=7\]이 두 식은 아래와 같은 연립방정식을 푸는 것과도 같다.
\[\begin{bmatrix}e^3 & e\\ e^9 & e^3\end{bmatrix}\begin{bmatrix}c_1 \\ c_2\end{bmatrix} = \begin{bmatrix}2 \\7\end{bmatrix}\]따라서, $c_1$과 $c_2$는 아래와 같이 결정되고,
\[\Rightarrow c_1 = -0.0010\text{, } c_2 = 0.7430\]해석적으로 구한 solution curve의 식은 다음과 같다. 여기서 $y(t)$는 $y(t) = x’(t)$와 같은 방법으로 결정되었다.
\[\begin{cases}x(t) = -0.001e^{3t}+0.7430e^{t} \\ y(t) = -0.003e^{3t}+0.7430e^{t}\end{cases}\]
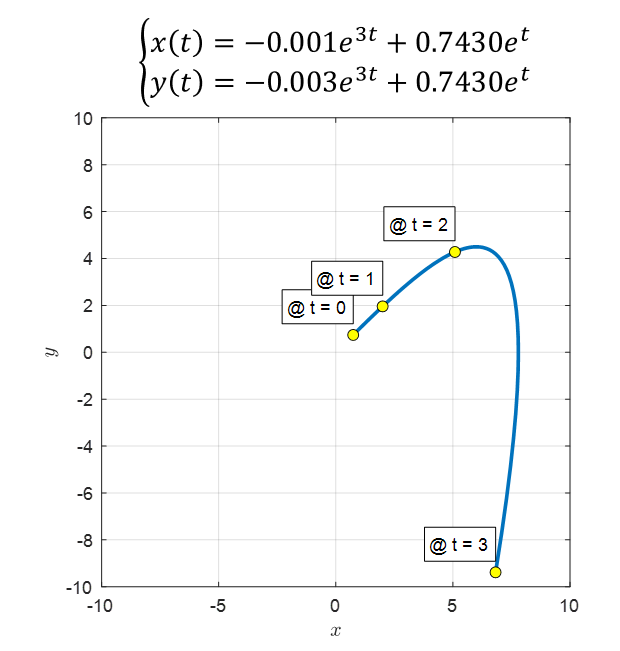
그림 3. 주어진 경계값 문제에 대한 solution curve
이 솔루션 커브는 그림 2에 그려진 ODE solver를 이용해 그려본 curve와 거의 유사한 형태를 띄고 있음을 알 수 있다.