어떤 집단의 before / after를 비교하려고 할 때는 어떤 통계 기법을 사용할 수 있을까?

이 포스팅은 Primer of Biostatistics, S. Glantz, 7판을 참고하여 작성하였습니다.

Prerequisites

이 포스팅을 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 표본과 표준 오차의 의미
• t-value의 의미와 스튜던트의 t-test

Motivation

이전의 포스팅 중 t-value의 의미와 스튜던트의 t-test에서는 두 표본 그룹을 통계적으로 비교하는 방법 중 하나로 t-test를 소개한 바 있다. 이 때 소개한 t-test를 독립 표본 t-검정(independent sample t-test)이라고도 부르는데, 그 이유는 서로 독립적으로 추출한 두 샘플 그룹 간의 비교를 수행하기 때문이다.

그런데, 간혹 실험을 수행하다보면 동일 피험자에 대해 before / after를 비교해보고 싶은 때가 생긴다. 가령, 다이어트 약의 효능이라던가 금연 효과 같은 실험이 그렇다고 할 수 있다. 만약 동일 피험자에 대해 before / after를 통계적으로 비교할 수 있다면, 각 사람에 대한 효과를 확인할 수 있으므로 더 민감하게 처치 효과를 확인해볼 수 있을 것이다.

이렇듯 동일 피험자들에 대한 before / after 를 통계적으로 비교해볼 수 있게 하는 모수 통계 기법으로 대응 표본 t-검정(paired t-test)를 소개하고자 한다.

paired t-test 설명

앞서 Motivation 파트에서는 동일 피험자에게 수행한 처치에 대해 before / after 비교가 가능하다면 더 효과적으로 처치 효과에 대한 검증이 가능하다고 하였는데, 이 말의 의미가 어떤 것인지 예시를 들어가며 구체적으로 더 알아보도록 하자.

아래의 그림 1은 이뇨제(소변이 더 잘나오게 하는 약)의 효과를 확인해보기 위한 실험 결과를 도시해놓은 것이다.

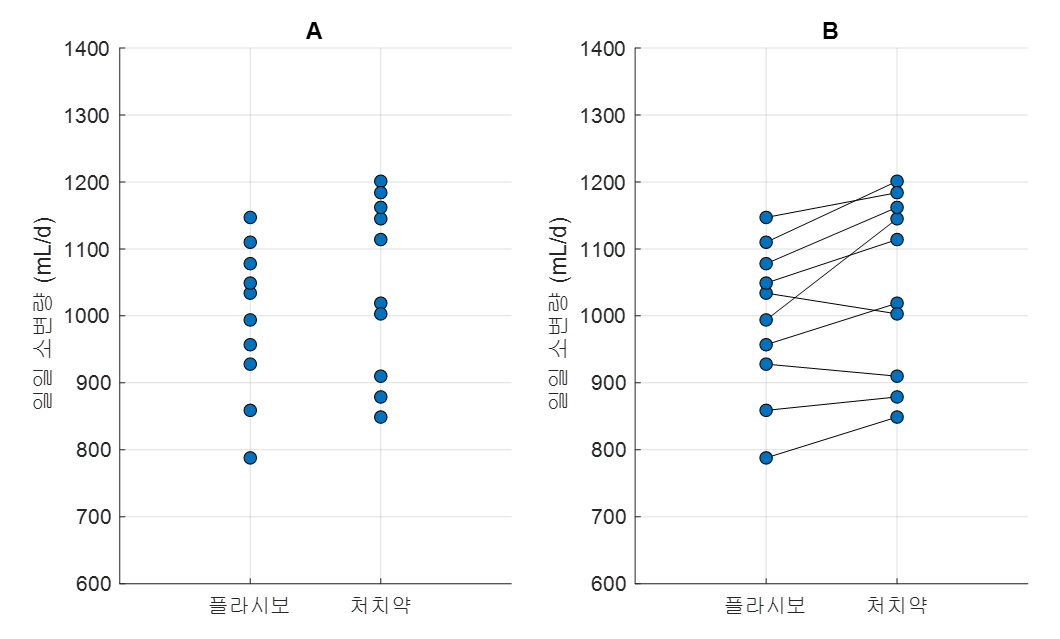
그림 1. 이뇨제의 처치 효과를 관찰하기 위한 실험 결과
이 그림은 Primer of biostatistics, 7th ed., S. Glantz의 Figure 9-1을 참고하여 만든 것 입니다.

그림 1을 보면 왼쪽(A) 그림과 오른쪽(B) 그림에서 차이점을 쉽게 확인할 수 있다. 줄이 그어져있는지 여부이다. 왼쪽(A) 그림은 플라시보(placebo)와 약물(drug) 그룹이 서로 독립적으로 추출된 표본 그룹임을 상정한 경우이다. 반면, 오른쪽(B) 그림은 동일한 표본 그룹의 피험자들에게 플라시보(placebo)와 약물(drug)을 한번씩 처치하여 실험이 진행된 것을 상정하고 있다.

독립 표본 t-검정으로 해석

그림 1의 왼쪽(A)의 상황에서 t-test를 진행해보도록 하자.

두 그룹의 평균은 각각 994.4와 1046.6이다. 그리고 각 그룹의 표준편차는 113.0046과 132.7983이므로 t-value를 계산해보면¹

\[t=\frac {\bar{X}_1 - \bar{X}_2} {\sqrt{s_1^2/{n_1^2} + s_2^2/{n_2^2}}}=-0.9467\]

이다. 여기서 $n_1, n_2$는 모두 10이다.

자유도(degree of freedom)는 $n_1+n_2-2=18$이다. 양측검정 t-test를 한다고 했을 때 유의한 t-value의 기준은 $t_{0.05}=-2.101$이다. 따라서 우리에게 주어진 $t$ 값인 $-0.9467$은 $-2.101$에 한참 못미치는 수치라고 할 수 있다. 즉, 이런 방식으로 통계 분석이 진행된다면 이 약은 이뇨제로써 작용하지 못한다고 결론지을 수 밖에 없다.

대응 표본 t-검정으로 해석

그런데 그림 1의 오른쪽(B) 상황을 보면 이 실험 결과가 어떻게 보이는지 차근히 살펴보자. 총 10명의 피험자 중 2명만이 투약 후 소변량이 감소했고 8명은 소변량이 증가한 것을 볼 수 있다. 이렇게 개개인에게 발휘된 처치 효과를 놓고 보면 이 약은 분명 이뇨제로써 잘 작용한다고 결론을 바꿀 수 있을 것이다.

따라서 우리는 그림 1의 오른쪽(B)에서 볼 수 있는 before / after의 차이에 관한 effect를 통계량으로 만들어보자.

t-value의 의미와 스튜던트의 t-test 편에서 t-value의 근본적 의미는 “차이/불확실도”라고 언급한 바 있었다. 간략하게만 복습하자면 표본 평균은 항상 오차를 수반하고 있으므로 발생하는 오차를 염두하면서 평균값 차이에 관한 지표를 만들어야 한다고 설명했다. 따라서 이번에도 마찬가지의 논리로 다음과 같이 t-value를 생각할 수 있다.

\[\text{(paired test) }t = \frac{\text{차이값의 평균}}{\text{차이 평균의 표준 오차}}\]

차이(difference)라는 의미에서 차이값의 평균을 $\bar{d}$라고 이름 붙이면 다음과 같이 t-value를 표현할 수 있다.

\[t=\frac{\bar{d}}{s_{\bar{d}}}\]

여기서 $\bar{d}$에 대한 표준오차로써 $s_{\bar{d}}=s_d/\sqrt{n}$이다.

생각해보면 independent t-test나 paired sample t-test나 논리는 차이를 불확실성으로 나눠준다는 점에서 같다.

실제로 paired t-test를 염두하여 문제를 풀어보자.

플라시보와 투약 시의 일일 소변량은 다음과 같다.

\[\text{플라시보}= [788, 859, 928, 957, 994, 1034, 1049, 1078, 1110, 1147]\] \[\text{투약 시} = [849, 879, 910, 1019, 1145, 1003, 1114, 1162, 1201, 1184]\]

따라서 플라시보 - 투약 의 차이값을 구하면 다음과 같다.

\[d = \text{플라시보}-\text{투약}=[-61, -20, 18, -62, -151, 31, -65, -84, -91, -37]\]

그러므로 $\bar{d}$는 위 $d$의 평균이므로 다음과 같고,

\[\bar{d} = -52.2\]

$s_{\bar{d}}$는 $d$의 표준 편차를 $d$의 개수의 제곱근으로 나눠준 것이므로

\[s_{\bar{d}} = \frac{s_d}{\sqrt{n}}=\frac{53.4723}{\sqrt{10}}=16.9094\]

따라서, t-value는

\[\text{(paired test) }t=\frac{-52.2}{16.9094}=-3.0870\]

임을 알 수 있다.

이 값은 유의한 차이라고 볼 수 있는 t-value의 기준인 $t_{0.05}=-2.2622$(자유도: 9, 양측검정)에 비해서 더 작은 값이므로 플라시보와 투약 조건 간에 유의한 소변량의 차이를 보인 것이라고 판단내릴 수 있다.

참고문헌

• Primer of biostatistics, 7th ed., S. Glantz / Ch. 9 Experiments when each subject receives more than one treatment