주파수 해상도란 무엇인가?
주파수 해상도란 원하는 신호를 주파수 domain에서 관찰할 때 얼마나 촘촘한 간격으로 해당 주파수 대역의 값을 관찰 할 수 있는가를 말한다고 할 수 있다. 이것은 time signal을 sampling 할 때 높은 샘플링 주파수를 가지고 신호를 기록하면 촘촘한 time signal을 얻을 수 있는 것과 유사한 개념이다.
보통 주파수 해상도에 대해서 얘기할 때 관찰하는 time window의 길이가 길면 frequency domain에서는 주파수 해상도가 좋고(즉, frequency domain에서 촘촘하게 관찰할 수 있고), sampling rate이 높으면 time domain에서 촘촘하게 관찰할 수 있다고 말한다. 이 내용이 처음에 듣기에는 다소 아리송할 수 있다. 이 내용에 대해 조금 더 자세하게 알아보도록 하자.
모든 Fourier Analysis는 Fourier Series에서 출발한다. 주기가 $T$인 함수 $f(t)$를 관찰한다고 했을 때, 각각의 주파수 값에 해당하는 weight는 다음과 같이 알 수 있다고 했다.
\[a_k = \frac{1}{T}\int_{-\infty}^{\infty}f(t) \exp(-j2\pi \frac{k}{T}t)dt\]따라서, 주기함수를 분석했을 때 주기의 길이에 따라 frequency domain에서 얼마나 촘촘한 간격으로 주파수를 볼 수 있는지 확인할 수 있는 것이다. 왜냐하면 $a_k$는 $\frac{1}{T}$ 만큼의 간격을 가지고 그려지기 때문이다. (exponential term 내부의 k는 정수이기 때문)
그림1은 그런 사실을 잘 표현해주고 있다. 이 때 frequency domain의 정의역은 정수 $k$이지만 우리는 $\frac{1}{T}$가 $df$로 표현될 수 있다는 사실을 알고 있다. 따라서, Fourier Series에서 확인할 수 있듯이 Time domain에서 신호의 주기가 frequency domain에서의 $df$ 값을 결정하게 되고 이것은 바로 주파수 해상도를 의미하게 되는 것이다.
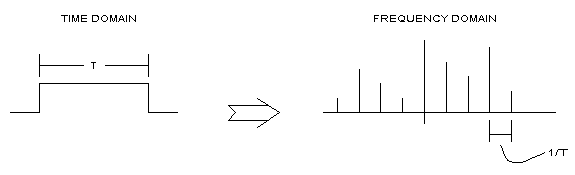
그림 1. 시간 window의 길이와 주파수 해상도. 주파수 해상도는 (1/T)로 표현된다.
출처: http://www.skylondaworks.com/sc_resol.htm
그런데, 여기서 중요한 질문이 생길 수 있다. 그것은 바로 우리가 얻게되는 혹은 분석하게 되는 신호는 완벽한 주기 신호가 아니며, 아날로그 신호가 아닌 digital 신호이기 때문에 Fourier Series를 이용해서만은 Short Time Fourier Transform(이하 STFT)의 frequency resolution을 다 설명할 수 없다는 것이다. 그렇기 때문에 DFT의 원리에 대해 간단하게 알아보고, STFT에서 왜 window size에 의해 frequency resolution이 결정되는 것인지 좀 더 자세히 알아보자.
Discrete Fourier Transform의 원리
DFT(Discrete Fourier Transform)는 비주기 신호를 컴퓨터 또는 디지털 기기를 사용해 해석하는데 쓸 수 있도록 Discrete Time Fourier Transform(이하 DTFT)을 변형시킨 것이다. DTFT를 컴퓨터에서 바로 사용할 수 없는 주된 원인은 무엇일까? 그것은 Time은 sample되어 있지만 (Discrete Time - 이라는 말이 붙은건 괜한 것이 아니다.) frequency는 sampling 되어 있지 않기 때문이다. DFT와 DTFT의 식은 다음과 같다.
\[X_{DFT}[k] = \sum_{n=0}^{N-1}x[n]\exp(-j2\pi \frac{k}{N}n)\quad(k는 정수)\] \[X_{DTFT}(f) = \sum_{n=-\infty}^{\infty}x[n]\exp(-j2\pi fn)\]즉, DFT의 식은 DTFT의 식에서 연속주파수 $f$를 $N$개로 나누어 준 것이다. 이 때 나오는 DFT의 $N$은 MATLAB에서 사용하는 NFFT를 뜻한다. (FFT와 DFT는 알고리즘 상의 차이는 있지만 원리는 동일)
DFT의 작동 원리를 후려쳐서 설명하자면 다음과 같다1. 길이가 T samples인 신호 $x[n]$에 대해서 주파수가 $1/T$인 코사인 함수 $\cos(2\pi\frac{1}{T}n)$을 곱한다. 곱해서 나온 결과를 $a_1$이라고 하고 저장한다. 이와 같은 방법으로 이후 주파수가 $k/T$ where $k=1, 2, \cdots, N$인 코사인함수를 준비해서 원래 신호 $x[n]$에 곱해주어 나온 값을 $a_k$ where $k=1,2,\cdots,N$ 이라 하고 저장한다. 이 방법을 사인함수에 대해서도 시행하고 출력된 값을 $b_n$이라고 한다.
그렇게 되면 $a_k$와 $b_k$가 의미하는 것은 무엇인가? 이것은 $a_k$ 또는 $b_k$는 각각 신호 $x[n]$ 이 주파수가 $k/T$인 cosine, sine 신호와 닮은 정도가 얼마인지를 나타내주게 된다 2.
그리고 이 때 허수 $j$에 대하여 $X[k] = a_k- jb_k$라고 쓰게 되면3, 결국 이것은 위의 DFT 식인
\[X_{DFT}=\sum_{n=0}^{N-1}x[n]\exp\left(-j2\pi\frac{k}{N}n\right)\]과 같은 의미를 가진다는 것을 알 수 있다4.
따라서, $a_k$와 $b_k$은 $X_{DFT}[k]$에서 각각 real component의 값과 imaginary components의 값을 의미하게 되고, 주파수 도메인에서 $\sqrt{a_k^2+b_k^2}$가 amplitude를, $\tan^{-1}(b_k/a_k)$이 phase를 의미하게 될 것이다.
time window의 길이가 주파수 해상도를 결정하는 이유
다시 우리의 원래 문제로 돌아와서 그렇다면 STFT에서 window의 길이를 정해주는 것이 주파수 해상도에 왜 영향을 주는 것일까?
그것은 Short Time Fourier Transform의 목적을 달성하기 위해서는 신호 전체 길이에 비해 짧은 window를 생각할 수 밖에 없게 되기 때문이고, 또한 DFT의 원리에 의하면 컴퓨터가 표현할 수 있는 주파수는 time window의 길이 $T$에 대해 $1/T$의 정수배일 수 밖에 없기 때문이다.
-
매우 좋은 설명 동영상으로 https://www.youtube.com/watch?v=h6QJLx22zrE 를 참고하기를 권한다. ↩
-
벡터와 함수의 내적은 모두 두 벡터나 함수를 (element by element) 곱해주는 것에서 시작했다는 것을 잊지 말도록! ↩
-
+j가 아닌 –j를 곱하는 것은 X[k]의 내부 exponential term에 –j가 있기 때문임. 왜 exponential term 안에 –j가 있어야 하는지 이해가 안 된다면 Fourier Series를 참고해보길 바람 ↩
-
즉, DFT의 식은 $x[n]$과 $\exp(-j2\pi\frac{k}{N}n)$에 대해 element by element 곱을 해줘서 더한 것과 같다. 그러므로 이것은 벡터의 내적과 같은 의미이고, 이산함수의 내적과도 같은 것이 된다. 이것은 우리가 $a_k$와 $b_k$를 구할 때 해준 방법과 같은 결과를 얻을 수 있게 해준다. ↩