최대우도법(MLE)

어떤 평균값을 갖는 확률밀도로 부터 이 샘플들이 추출되었을까?
adapted from the Seeing Theory's amazing visualization of MLE

최대우도법의 정의

최대우도법(Maximum Likelihood Estimation, 이하 MLE)은 모수적인 데이터 밀도 추정 방법으로써 파라미터 $\theta = (\theta_1, \cdots, \theta_m)$으로 구성된 어떤 확률밀도함수 $P(x|\theta)$에서 관측된 표본 데이터 집합을 $x = (x_1, x_2, \cdots, x_n)$이라 할 때, 이 표본들에서 파라미터 $\theta = (\theta_1, \cdots, \theta_m)$를 추정하는 방법이다.

당연히, 이 말만 보면 MLE가 뭔지 이해하기는 불가능하기 때문에 예시를 들어 MLE에 대해 알아보도록 하자.

MLE의 toy example 예시

MLE의 핵심 아이디어를 이해하기 위해 아래와 같은 매우 간단한 toy example을 생각해보자.

다음과 같이 5개의 데이터를 얻었다고 가정하자.

\[x = \lbrace1,4,5,6,9\rbrace\]

이 때, 아래의 그림을 봤을 때 데이터 $x$는 주황색 곡선과 파란색 곡선 중 어떤 곡선으로부터 추출되었을 확률이 더 높을까?

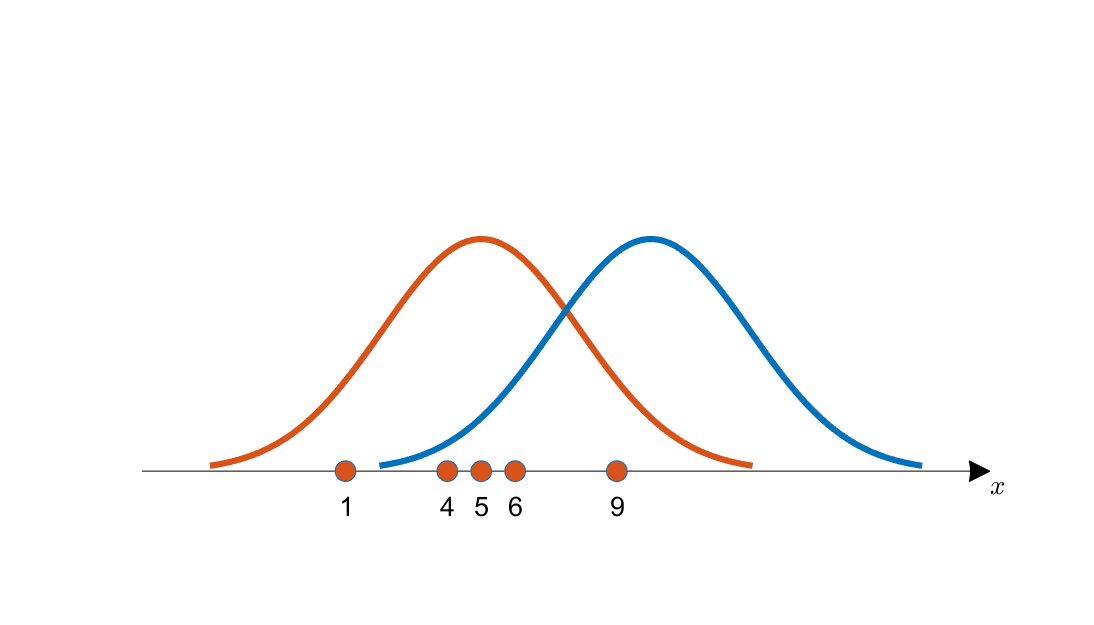
그림 1. 획득한 데이터와 추정되는 후보 분포 2개(각각 주황색, 파란색 곡선으로 표시)

눈으로 보기에도 파란색 곡선 보다는 주황색 곡선에서 이 데이터들을 얻었을 가능성이 더 커보인다.

왜냐면 획득한 데이터들의 분포가 주황색 곡선의 중심에 더 일치하는 것 처럼 보이기 때문이다.

이 예시를 보면, 우리가 데이터를 관찰함으로써 이 데이터가 추출되었을 것으로 생각되는 분포의 특성을 추정할 수 있음을 알 수 있다. 여기서는 추출된 분포가 정규분포라고 가정했고, 우리는 분포의 특성 중 평균을 추정하려고 했다.

그럼 좀 더 구체적으로, 수학적인 방법으로 정밀하게 이 분포의 특성을 추정하는 방법을 이해해보도록 하자.

Likelihood function

앞서 언급한 수학적인 추정방법을 언급하기 위해 데이터의 likelihood 기여도에 대해 얘기해보자.

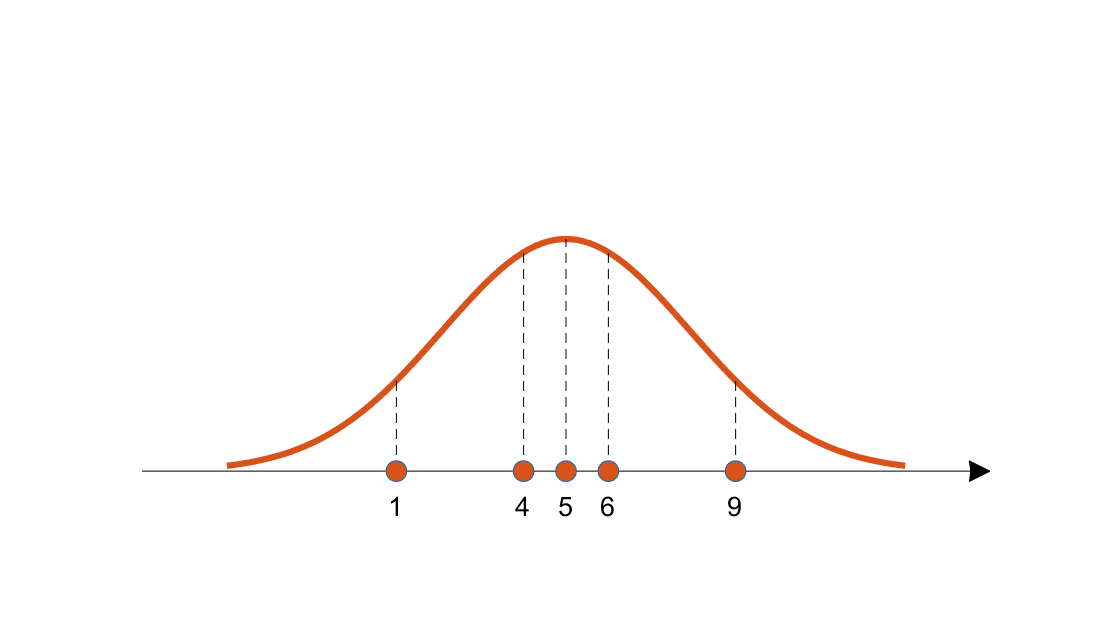
그림 2. 주황색 후보 분포에 대해 각 데이터들의 likelihood 기여도를 점선의 높이로 나타냈다.

likelihood 라는 것은 특별히 어려운 것이 아니고, 지금 얻은 데이터가 이 분포로부터 나왔을 가능도를 말한다.

수치적으로 이 가능도를 계산하기 위해서는 각 데이터 샘플에서 후보 분포에 대한 높이(즉, likelihood 기여도)를 계산해서 다 곱한 것을 이용할 수 있을 것이다.

계산된 높이를 더해주지 않고 곱해주는 것은 모든 데이터들의 추출이 독립적으로 연달아 일어나는 사건이기 때문이다.

그렇게 해서 계산된 가능도를 생각해볼 수 있는 모든 후보군에 대해 계산하고 이것을 비교하면 우리는 지금 얻은 데이터를 가장 잘 설명할 수 있는 확률분포를 얻어낼 수 있게 된다.

지금까지 얘기한 likelihood를 조금 더 수학적으로 서술하면 다음과 같이 쓸 수 있다.

아래와 같이 전체 표본집합의 결합확률밀도 함수를 likelihood function이라고 한다.

\[P(x|\theta) = \prod_{k=1}^{n}P(x_k|\theta)\]

위 식의 결과 값이 가장 커지는 $\theta$를 추정값 $\hat{\theta}$로 보는 것이 가장 그럴듯하다.

위 식을 likelihood function이라고 하고 보통은 자연로그를 이용해 아래와 같이 log-likelihood function $L(\theta | x)$를 이용한다.

\[L(\theta| x) = \log P(x|\theta) = \sum_{i=1}^{n}\log P(x_i | \theta)\]

Likelihood function의 최대값을 찾는 방법

결국 Maximum Likelihood Estimation은 Likelihood 함수의 최대값을 찾는 방법이라 할 수 있다.

log 함수는 단조증가 함수이기 때문에 likelihood function의 최대값을 찾으나 log-likelihood function의 최대값을 찾으나 두 경우 모두의 최대값을 갖게 해주는 정의역의 함수 입력값은 동일하다.

따라서, 보통은 계산의 편의를 위해 log-likelihood의 최대값을 찾는다.

어떤 함수의 최대값을 찾는 방법 중 가장 보편적인 방법은 미분계수를 이용하는 것이다.

즉, 찾고자하는 파라미터 $\theta$에 대하여 다음과 같이 편미분하고 그 값이 0이 되도록 하는 $\theta$를 찾는 과정을 통해 likelihood 함수를 최대화 시켜줄 수 있는 $\theta$를 찾을 수 있다.

\[\frac{\partial}{\partial \theta}L(\theta|x) = \frac{\partial}{\partial \theta}\log P(x|\theta) = \sum_{i=1}^{n}\frac{\partial}{\partial\theta}\log P(x_i|\theta) = 0\]

MLE의 좀 더 복잡한 예시 (모평균, 모분산 추정)

평균 $\mu$와 분산 $\sigma^2$를 모르는 정규분포에서 표본 $x_1, x_2, \cdots, x_n$을 추출했을 때, 이들 값을 이용해서 모분포의 평균과 분산을 추정해보자. 익히 들어서 알겠지만 표본을 위와 같이 추출하였다고 하면 모평균의 추정값은

\[\hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i\]

이고 모분산의 추정값은

\[\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}\left(x_i-\mu\right)^2\]

이다. 이것을 최대우도법을 이용해서 확인해보도록 하자.

각각의 표본들은 정규분포에서 추출된다고 했을 때 각 표본의 표본분포는

\[f_{\mu, \sigma^2}(x_i) = \frac{1}{\sigma\sqrt{2\pi}} \exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)\]

이고, $x_1, x_2, \cdots, x_n$은 모두 독립적으로 추출했다고 가정하자. 그러면 우도(likelihood)는

\[P(x|\theta) = \prod_{i=1}^{n}f_{\mu, \sigma^2}(x_i) = \prod_{i=1}^{n}\frac{1}{\sigma\sqrt{2\pi}} \exp \left( -\frac{(x_i-\mu)^2}{2\sigma^2} \right)\]

이고, 로그-우도는

\[L(\theta|x) = \sum_{i=1}^{n}\log\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x_i-\mu)^2}{2\sigma^2}\right)\] \[=\sum_{i=1}^{n}\lbrace \log\left( \exp(-\frac{(x_i-\mu)^2}{2\sigma^2}) \right) - \log\left( \sigma\sqrt{2\pi} \right) \rbrace\] \[=\sum_{i=1}^{n}\left\lbrace -\frac{(x_i-\mu)^2}{2\sigma^2}-\log(\sigma) - \log(\sqrt{2\pi}) \right\rbrace\]

이다. 따라서 $L(\theta|x)$를 $\mu$에 대해 편미분하면,

\[\frac{\partial L(\theta|x)}{\partial \mu} =-\frac{1}{2\sigma^2}\sum_{i=1}^{n}\frac{\partial}{\partial \mu}\left(x_i^2-2x_i\mu+\mu^2\right)\] \[=-\frac{1}{2\sigma^2}\sum_{i=1}^{n}\left(-2x_i+2\mu\right)\] \[=\frac{1}{\sigma^2}\sum_{i=1}^{n}(x_i-\mu) = \frac{1}{\sigma^2}\left(\sum_{i=1}^{n}x_i-n\mu\right) = 0\]

따라서 최대우도를 만들어주는 모평균의 추정량은

\[\hat{\mu} = \frac{1}{n}\sum_{i=1}^{n}x_i\]

이다.

한편, $L(\theta|x)$를 표준편차 $\sigma$로 편미분하면

\[\frac{\partial L(\theta|x)}{\partial \sigma} = -\frac{n}{\sigma} - \frac{1}{2}\sum_{i=1}^{n}\left(x_i-\mu\right)^2\frac{\partial}{\partial\sigma}\left(\frac{1}{\sigma^2}\right)\] \[=-\frac{n}{\sigma}+\frac{1}{\sigma^3}\sum_{i=1}^{n}\left(x_i-\mu\right)^2 = 0\]

따라서, 최대우도를 만들어주는 모분산의 추정량은

\[\hat{\sigma}^2 = \frac{1}{n}\sum_{i=1}^{n}\left(x_i-\mu\right)^2\]

이라는 것을 알 수 있다.