※ 본 포스팅의 내용은 Thomas Judson의 The ordinary differential equations project에서 많은 부분을 차용하였음을 밝힙니다.

미분방정식은 방정식 안에 미분계수가 포함되어 있는 것을 말한다.

이 때, 미분 계수의 미분 횟수는 1회에서 그치지 않고 여러회 반복될 수 있는데,

가장 간단한 1계 미분방정식(first-order differential equation)의 경우의 형식은 다음과 같다.

\[\frac{dy}{dx}=f(x, y) % 식 (1)\]

우리는 이번 포스팅에서 식 (1)과 같은 미분방정식이 어떻게 나올 수 있었는지를 차근히 알아보고자 한다.

Exponential Growth

미분은 ‘변화’에 대한 수학적 서술이다.

상상하기 좋은 변화에 대한 예시 중 하나는 성장인데, 인구 성장에 대한 예시를 통해 미분방정식의 형태를 이끌어내보자.

인구는 기하급수적으로 성장한다. 말이 어려운데, 이것을 풀어서 생각해보면 이렇게도 생각할 수 있다.

인간들은 인구 중 일부가 출산을 하고, 인구 중 일부가 사망함으로써 인구가 성장한다.

그럼 인구의 성장량은

\[\text{성장 인구 수 }=\text{ 출산 인구 수 } - \text{사망 인구 수} % 식 (2)\]

와 같이 표현할 수 있다.

이 때, 우리는 시간에 대해 생각하고 있지 않았다는 것을 알 수 있다. 중요한 포인트인데, 우리는 성장량을 ‘단위 시간 동안의 성장’에 대해 생각해야 한다는 점을 간과하면 안된다.

만약 저 식 (2)의 성장량이 100만년 동안의 성장인지, 1년 간의 성장인지 적어 두지 않으면 어떤 의미가 있단 말인가?

그래서 식 (2)를 다음과 같이 수정해 볼 수 있다.

\[\text{특정 시간 동안의 성장 인구 수 }=\text{ 단위 시간 당 출산 인구 수 }\cdot\text{특정 시간} - \text{사망 인구 수}\cdot\text{특정 시간} % 식 (3)\]

식 (3)은 너무 장황하게 한글로 써둔 식이다. 이것을 수학적 표현으로 고쳐써보자.

단위 시간 당 출산인구 수는 현재 인구에 비례할 것이다. 왜냐면, 현재 생존 인구 중 일부만이 출산할 것임을 알 수 있기 때문이다. 단위 시간 당 사망 인구 수도 현재 인구에 비례하는 값임을 쉽게 유추할 수 있다.

시간에 따른 인구수를 $P(t)$라고 하고, 특정 시간 동안 성장한 인구 수를 $\Delta P$라고 하자.

그리고 출산 인구의 비율을 $k_\text{birth}$, 사망 인구의 비율을 $k_\text{death}$라고 하면 아래와 같은 식을 생각할 수 있다.

\[\text{식(3)}\Rightarrow\Delta P \approx k_\text{birth}P(t)\Delta t-k_\text{death}P(t)\Delta t % 식 (4)\]

식 (4)를 살짝 고쳐서 $k = k_\text{birth} - k_\text{death}$라고 하면,

\[\Rightarrow \Delta P \approx kP(t)\Delta t % 식 (5)\]

와 같이 쓸 수 있으므로 양변을 $\Delta t$로 나눠주면 아래와 같은 식을 얻게 됨을 알 수 있다.

\[\frac{\Delta P}{\Delta t}\approx k P(t) % 식 (6)\]

식 (6)의 의미는 단위 시간 당 인구수의 변화는 현재 인구수에 비례한다는 뜻이다.

식 (6)에 대해 $\Delta t$를 매우 작게 만들어주면 미분방정식을 얻을 수 있게 된다.

\[\Rightarrow \lim_{\Delta t \rightarrow 0}\frac{\Delta P}{\Delta t}=\frac{dP}{dt}% 식 (7)\]

이므로,

\[\therefore \frac{dP}{dt}=kP % 식 (8)\]

위 식은 식 (1)에서 보여준 미분 방정식의 형태와 같다는 것을 알 수 있다.

식 (8)의 미분방정식의 솔루션은

\[P(t) = Ce^{kt} % 식 (9)\]

임을 알 수 있다.

식 (9)를 식 (8)에 다시 대입해보면

\[Cke^{kt} = kCe^{kt} % 식 (10)\]

가 성립한다는 것을 알 수 있기 때문이다.

여기서 만약 우리가 첫 시작 인구수를 알 수 있다면 식 (9)의 $C$ 값을 특정할 수도 있을 것이다.

가령, $t=0$일 때의 인구수가 $P_0$라고 한다면,

\[식(9)\Rightarrow P(t) = P_0e^{kt} % 식 (11)\]

임을 알 수 있는것이다.

Logistic growth

인구수는 기하급수적으로 성장한다는 말은 많이 들어봤을지 모르지만, 인구수의 성장에는 사실 한계가 있다.

최근 대한민국은 출산율 저하로 고민하고 있는데, 이런 추세의 성장률이라면 인구수 하락은 면치 못할 미래가 될 것이라는 것이 불보듯 뻔하다.

인구수는 왜 계속해서 커지지 못할까?

자원의 한계가 있기 때문이다.

페트리 디쉬에 있는 박테리아는 아무리 그 숫자가 많아지더라도 페트리 디쉬의 크기 이상을 벗어나기 힘든 것과 마찬가지이다.

그림 1. 페트리 디쉬 안에 있는 박테리아는 개체수에 한계가 있어 logistic growth 형태를 따라 성장해간다.

식 (8)을 조금 수정해서 성장할 수 있는 최대치에 가까워질 수록 성장량이 더뎌지는 모델을 만들어보자.

식 (8)에 다음과 같은 조치를 취해보자.

\[식 (8) \Rightarrow \frac{dP}{dt}=kP(1-\frac{P}{N}) % 식 (12)\]

즉, 식 (8)에서 $(1-P/N)$이라는 함수를 덧붙였다.

여기서 $N$은 최대 성장치로, 식 (12)가 말해주는 것은 인구수의 변화량은 $P$가 $N$에 다다를 수록 0에 가까워진다는 뜻으로 해석할 수 있다. 왜냐면 $(1-P/N)$은 $P=0$ 일 때는 $(1-P/N)=1$이지만 $P$가 $N$에 다다를 수록 $(1-P/N)=0$에 가까워질 것이기 때문이다.

이와 같은 모델의 솔루션은

\[P=\frac{N}{Ce^{-kt}+1} % 식 (13)\]

라고 알려져 있다. (식 (13)이 식 (12)에 대한 solution임은 직접 확인해보도록 하자.)

$N, C, k$에 적절한 값을 넣었을 때 그래프의 형태는 아래와 같다.

아래의 그래프에서는 $N=1000$이라는 값을 넣었는데, 이것이 말하는 것은 최대 수용 인구수가 1000이라는 뜻이다. 그래서 시간이 지날 수록 인구수는 1000에 수렴한 뒤 변화가 없는 것을 알 수 있다.

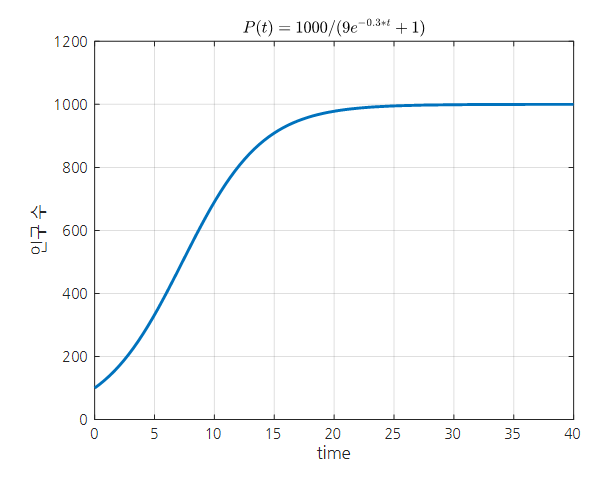
그림 2. logistic growth의 예시 그래프 중 하나

스프링의 움직임에 관한 현상

Undamped spring-mass system

후크의 법칙이라고 알려진 스프링의 움직임에 관한 식은 다음과 같다.

\[F = -kx % 식 (14)\]

여기서 음수가 붙은 것은 스프링이 늘어난 방향과 이 때 작용하는 힘의 방향이 반대라는 의미이다.

이러한 관계식은 다음과 같은 현상을 관찰하여 알게된 사실을 기반으로 한다.

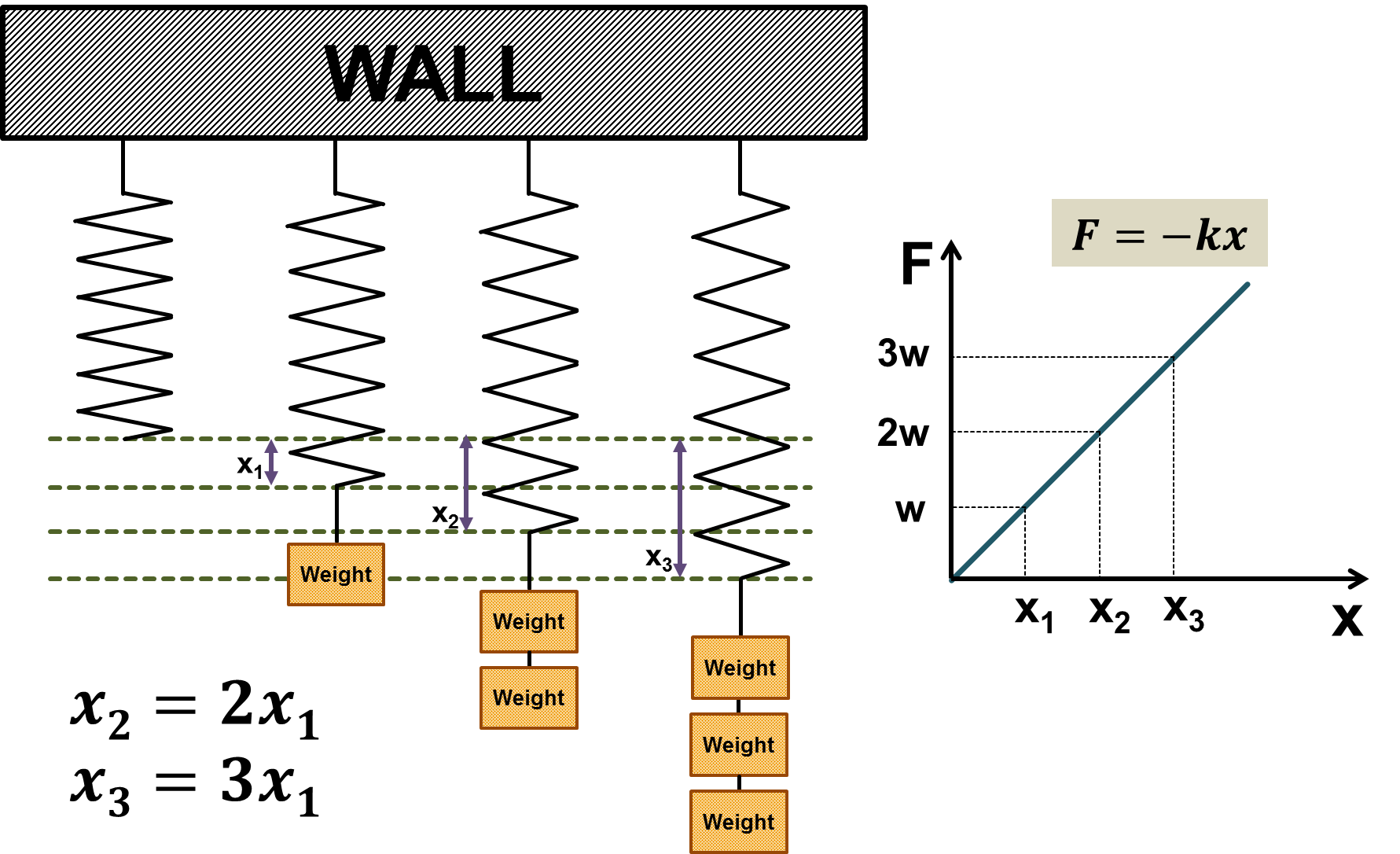
그림 3. 후크의 법칙 유도 실험
그림 출처: 훅 법칙 위키피디아

그림 3에서 보여주듯이 용수철은 늘여준 길이에 비례해 탄성력이 작용한다는 것을 실험적으로 알게되어서 그 현상을 식 (14)와 같이 설명한 것이다.

그럼 식 (14)는 미분방정식이라고 할 수 있는 것일까? 힘은 질량 x 가속도로 풀어쓸 수 있기 때문에 식 (14)는 다음과 같이도 쓸 수 있다.

\[m\frac{d^2x}{dt^2}=-kx % 식 (15)\]

즉, 식 (15)를 보면 후크의 법칙은 2계 미분방정식이었다는 것을 알 수 있다.

이 미분방정식에 대한 solution은 다음과 같다.

\[x(t) = A\cos(t) + B \sin(t) % 식 (16)\]

만약 $m=1$이고 $k=1$이라고 하고, $x(0) = 0$, $x’(0) = 1$이라는 조건을 부여했을 때 식(16)은

\[x(t) = \sin(t) % 식 (17)\]

라는 것을 알 수 있다.

후크의 법칙으로부터 유도되는 이 움직임은 보통 undamped spring-mass system의 움직임이라고 하고 때때로 harmonic motion이라고도 불린다.

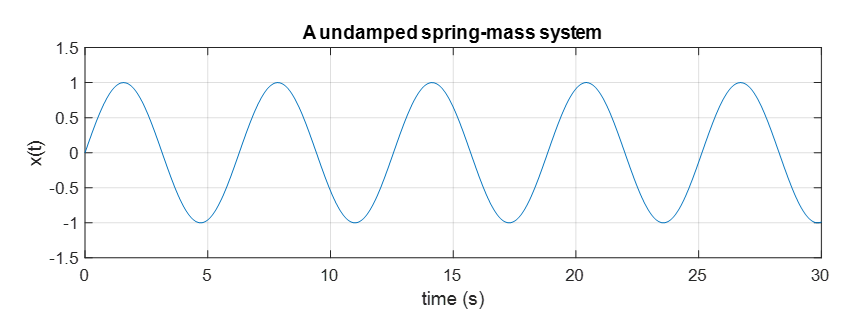
그림 4. damping이 없다고 가정한 경우의 스프링의 움직임은 sine 함수로 주어진다.

Damped spring-mass system

Damped motion에 대해 알아보기에 앞서서 damping이라는 것이 무엇인지 생각해보아야 한다.

damping은 물체를 빠르게 움직일 수록 더 큰 힘을 역으로 받게 해주는 시스템이다.

문을 확 잡아 당기거나 확 닫을 때 문이 오히려 더 천천히 열릴 수 있게 반대 방향으로 힘을 준다던지,

물체가 떨어질 때 천천히 떨어질 수 있게 만들어주는 경우에 이런 방법을 이용할 수 있다.

이렇게 움직임에 damping motion을 주는 기계를 dashpot이라고 한다. 아래의 영상을 보면 dashpot이 어떻게 쓰이는지 확인해볼 수 있다.

dashpot이 주어주는 damping motion은 속도에 반대되는 방향으로 주어지므로,

\[F = -b\frac{dx}{dt} \text{ where }b>0% 식 (18)\]

로 표현할 수 있다.

따라서, 기존의 식 (14)에 damping motion에 관한 식을 추가하면 다음과 같이 식이 변형된다.

\[식(14) \Rightarrow F = -kx - b\frac{dx}{dt} % 식 (19)\]

혹은

\[m\frac{d^2x}{dt^2}=-kx-b\frac{dx}{dt} % 식 (20)\] \[\Rightarrow m\frac{d^2x}{dt^2}+b\frac{dx}{dt}+kx =0 % 식 (21)\]

이런 모델을 simple damped harmonic oscillator라고 한다.

추후에 식 (21)과 같은 미분방정식을 어떻게 푸는지에 관해서 알게 되겠지만,

지금은 이 미분방정식의 solution이 아래와 같은 형태라고 생각하고 문제를 풀어보자.

\[x(t) = e^{rt} % 식 (22)\]

식 (22)를 식 (21)에 대입하면,

\[식 (21) \Rightarrow mr^2e^{rt}+bre^{rt}+ke^{rt}=0 % 식 (23)\]

over-damped spring-mass system

여기서 $m=1$, $b=3$, $k=2$라고 해보자.

그러면

\[\Rightarrow r^2e^{rt}+3re^{rt}+2e^{rt}=0 % 식 (24)\] \[\Rightarrow e^{rt}(r^2+3r+2)=0 % 식 (25)\] \[\Rightarrow e^{rt}(r+1)(r+2) = 0 % 식 (26)\]

여기서 생각해볼 수 있는 것은 $e^{rt}$는 항상 양수이므로, $r=-1$ 또는 $r=-2$이다.

따라서, 우리의 솔루션은 아래와 같은 형태여야 한다.

\[x(t) = Ae^{-t}+Be^{-2t} % 식 (27)\]

만약 initial value가 다음과 같이 주어졌다고 가정해보면,

\[x(0) = 0 % 식 (28)\] \[x'(0) = 1 % 식 (29)\]

다음과 같이 $A$와 $B$의 값을 계산할 수 있다.

\[x(0) = A+B = 0 % 식 (30)\] \[x'(t) = (-1)Ae^{-t}+(-2)Be^{-2t} % 식 (31)\] \[x'(0) = -1A-2B = 1 % 식 (32)\] \[\therefore A = 1, B = -1 % 식 (33)\]

따라서, 우리의 솔루션은

\[식(27)\Rightarrow x(t) = e^{-t}-e^{-2t} % 식 (34)\]

과 같다.

식 (34)의 경우를 그림으로 그려보면

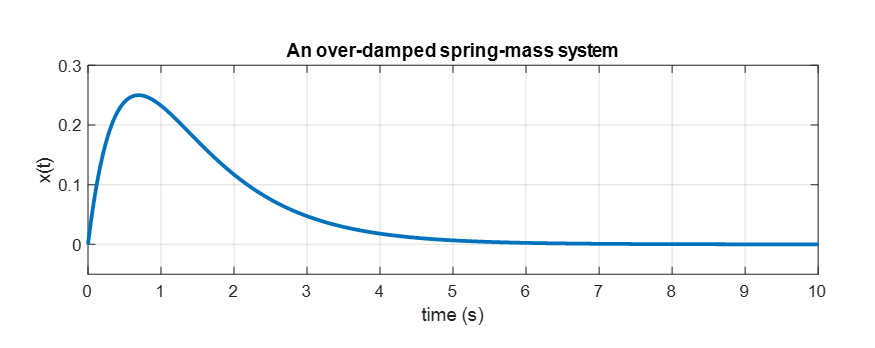
그림 5. spring의 힘에 비해 damping이 더 크게 주어진 경우. over-damped spring-mass system의 solution curve

under-damped spring-mass system

만약 $k=2$가 아니라 $k=38.25$이라고 생각해보자.

그 말은 스프링 힘이 굉장히 강력해서 조금만 힘을 주어도 팍팍 스프링이 늘어나도록 설계되어 있는 경우이다.

다시 말해, 댐핑은 스프링의 움직임에 작은 저항력과 같이 작용한다는 뜻이다.

다른 조건은 모두 같다고 했을 때 이 경우의 solution을 생각해보면,

\[\Rightarrow r^2e^{rt}+3re^{rt}+38.25e^{rt}=0 % 식 (35)\] \[\Rightarrow e^{rt}(r^2+3r+38.25) = 0\]

이 경우의 solution은

\[x(t) = e^{-\frac{3t}{2}}(A\cos(6t)+B\sin(6t))\]

이라는 것을 알 수 있는데, 식 (28), 식 (29)의 초기조건을 다시 넣어보면,

\[x(0) = A = 0\] \[x'(t) = (-3/2)e^{\frac{-3t}{2}}(B\sin(6t))+e^{\frac{-3t}{2}}(6B\cos(6t))\] \[\Rightarrow x'(0) = 6B = 1\]

따라서, solution curve는

\[x(t) = \frac{1}{6}e^{-\frac{3t}{2}}\sin(6t)\]

임을 알 수 있다.

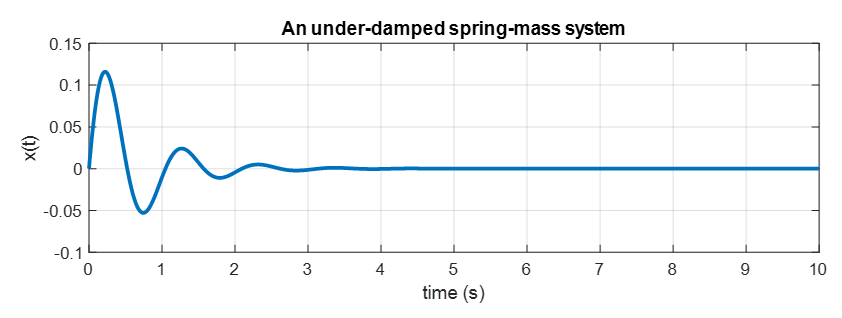
그림 6. damping에 비해 spring의 힘이 더 크게 주어진 경우. under-damped spring-mass system의 solution curve

마무리 하면서

이번 posting에서는 몇 가지 현상에 대해 미분방정식으로 모델링을 해보고 그 솔루션 커브를 구하는 과정을 확인했다.

미분 방정식은 대체로 솔루션을 구하는 방법에 대해 배우는 과목이라고 볼 수 있다. 당연한 얘기인지는 모르겠지만, 방정식을 배우면 방정식의 해를 구하는 과정을 배워야 하는 것은 당연한 흐름일 것이다. 앞으로 배우게 될 내용은 아래와 같은 것들이다.

• 위에서 과정들이 많이 생략된 솔루션을 구하는 방법들은 어떻게 알 수 있게 되는 것인지
• 이런 솔루션을 얻는 방법이 항상 작동하는 것인지
• 솔루션 풀이 법이 먹힌다고 해서 해는 유일하게 존재하는 것인지
• 솔루션이 존재하지만 저런 방법들 중 하나로 모든 미분 방정식을 풀 수 있게 되는 것인지