Prerequisites
이번 포스팅을 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
서론
이번 포스팅에서는 복소수의 기초 부분을 공부해보고자 한다. 특히, 복소 지수 함수와 복소수의 사칙 연산에 대해서 짚고 넘어가고자 한다.
허수와 복소수는 중학교 과정에서 처음 등장했던 것으로 기억한다. 그 당시 논리적으로는 허수와 복소수의 존재를 납득할 수 있겠으나 그 쓰임에 대해서는 전혀 알려주지 않고 넘어가는 대한민국의 수학공부 방식 때문인지는 몰라도 복소수를 직접 써먹을 수 있으리라는 생각은 해보지 못했던 것 같다.
신호처리 분야에서는 많은 경우 복소수를 이용해 신호를 표현한다. 그 이유는 선형시불변(Linear Time Invariant) 시스템에 대해 복소 지수함수가 고유함수(eigenfunction)로 작동하기 때문이다. 조금만 더 쉽게 풀어쓰면 복소 지수함수가 입력으로 들어가면 항상 출력은 같은 주파수의 복소 지수함수가 나온다는 것이다. 이 말을 지금은 잘 이해하지 못할 수 있기 때문에 자세한 설명은 추후에 더 들어보도록 하자.
어찌되었든 위의 이유로 신호처리 분야에서 신호를 다룰 때는 복소 신호를 이용하는 것이 편하다. 처음에는 멀쩡한 실수 신호를 놔두고 왜 복소 신호를 쓸까 하면서 불편해할 수도 있지만, 막상 복소 신호를 이용한 풀이를 공부한 뒤 이걸 실수 신호로 바꿔 쓰려고 하면 도저히 감당이 되지 않는 연산량에 혀를 내두르게 될 것이다.
마지막으로 이 포스팅에서는 단위 허수를 $i$가 아닌 $j$로 쓴다 ($j^2=-1$). 이것은 전기공학 분야에서 전류를 $i$로 사용하는 관례에 따른 또 다른 관례이다.
복소수 표현 방법
허수의 존재 의미에 대하여 편에서 언급했듯이 허수 체계는 실수 축에 직교하는 수 체계이다.
그리고 복소수 체계는 실수 체계와 허수 체계를 합한 것이므로 실수 체계와 허수 체계를 각각 가로축과 세로축에 수직선으로 하는 복소 평면을 구성하고 그 위에 표현할 수 있다.
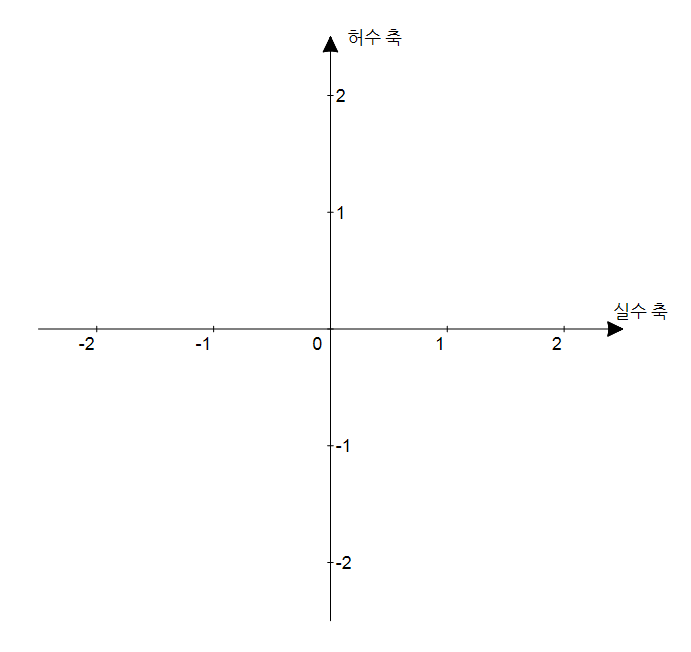
그림 1. 가로축과 세로축을 실수, 허수축으로 구성하면 복소평면을 얻을 수 있게 된다.
임의의 복소수, 예를 들어 $z=1+j0.5$라고 하면 $(1, 0.5)$ 좌표에 점을 찍어 복소수 하나를 표현할 수 있게 된다.
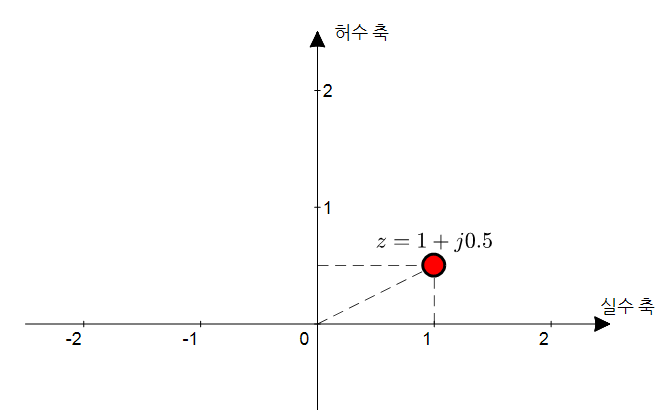
그림 2. 복소수는 복소 평면 위에 한 점으로 표현할 수 있다.
그런데, 복소수를 평면 상의 한 점이라고 놓고 보면 어떤 좌표계를 쓰는지에 따라 다르게 복소수를 표현할 수 있게 된다. 주요하게는 직각 좌표계와 극 좌표계를 사용해 복소수를 표현할 수 있다.
직각 좌표형
직각 좌표계를 이용해 복소수를 표현하는 것은 복소수를 실수부와 허수부로 나누어 표현해주는 것을 의미한다.
직각 좌표계는 보통 좌표계라고 할 때 생각할 수 있는 데카르트 좌표계(Cartesian coordinate)을 말한다.
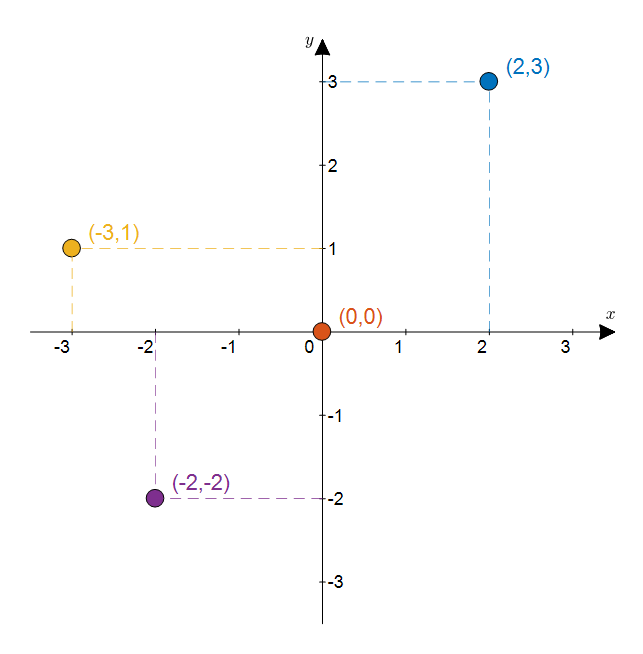
그림 3. 직각 좌표계 위에 표현된 네 개의 점
가령 그림 3과 같이 네 개의 점을 직각 좌표게에 표현해볼 수 있는데, 만약 이 평면이 복소평면이었다면 네 개의 점들은 각각 다음과 같은 복소수를 표현한 것이다.
\[(2,3): 2+j3\] \[(0, 0): 0+j0\] \[(-3,1): -3+j1\] \[(-2,-2): -2-j2\]즉, $x$ 좌표와 $y$ 좌표를 이용해 다음과 같이 하나의 복소수 포인트를 표현할 수 있게 된다.
\[x+jy\]극 좌표형
극 좌표계(polar coordinate)를 이용해 복소수를 표현하는 것은 복소수를 원점으로부터의 거리와 가로축에서부터의 각도를 이용해 표현해주는 것을 의미한다.
극 좌표계는 고등학교 수학을 배울 때 까지는 볼 일이 없던 좌표이기 때문에 생소할 수 있기 때문에 조금은 익숙해질 필요가 있는 좌표계이다.
가령 $z=1+j0.5$를 표현해주는 복소평면 위의 점에 대해 원점으로부터의 거리와 가로축으로부터의 각도를 계산해보면 다음과 같다.
\[r=\sqrt{1^2+0.5^2}=1.118\] \[\theta = \tan^{-1}\left(\frac{0.5}{1}\right)=0.4636 \text{ rad}\]즉, 아래의 그림에서 $r$과 $\theta$의 값은 $r = 1.118$과 $\theta = 0.4636 \text{ rad}$ 혹은 $\theta = 26.56°$이다.
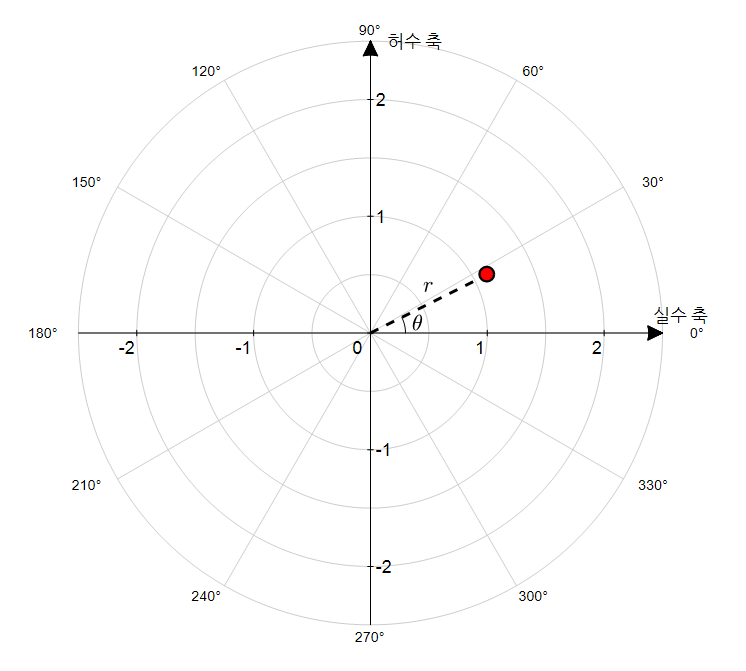
그림 4. 직각 좌표계에서 (1, 0.5)로 표시하던 점을 극 좌표계로 보려는 시도
생각해보면 1, 0.5 이렇게 단순한 숫자 두 개로 구성될 수 있었던 숫자들이 더 복잡해졌다. 그렇다면 왜 극좌표계를 이용해 복소수를 표현해보려고 하는 것일까?
복소수를 표현하는데 있어 극좌표계를 사용하는 이유는, 추후 더 알게 되겠지만 복소수는 회전과 관련이 있는 수체계이기 때문이다. 회전을 표현하는데 있어 극좌표계를 이용하면 조금 더 간략하게 표기할 수 있기 때문이다.
극 좌표계로 점을 표현할 때는 $(r, \theta)$와 같은 순서쌍으로도 표현할 수 있지만 혼란을 방지하기 위해 다음과 같은 표기를 이용하기도 한다.
\[r\angle \theta\]이 때 $\theta$의 표기에 관해 주의할 점은 $\theta$는 $2\pi$ 라디안 혹은 360도를 주기로 하는 각도라는 점이다. 극좌표형의 표기에서 $\theta$는 $-\pi<\theta<\pi$ 혹은 $-180°\lt \theta \lt 180°$ 사이의 각도로 표시하는 것이 관레이다. 만약 각도가 이 범위 안에 있지 않으면 360°의 배수를 더하거나 빼서 기본각의 범위 안에 들어가도록 만들어 표기해준다.
예를 들어, $3\angle 280°$ 는 360도를 빼줘서 $3\angle-80°$로 써주어야 한다.
두 좌표계 간의 변환
복소수를 표현할 때 직교 좌표계와 극 좌표계 둘 다 많이 사용되지만, 신호 처리를 공부할 때에는 극 좌표계를 더 자주 이용한다. 그 이유는 결국 정현파는 원의 회전으로부터 출발하는 개념이기 때문에 회전을 표현하기에 더 적합한 극좌표계를 사용하는 것이라고 볼 수 있다.
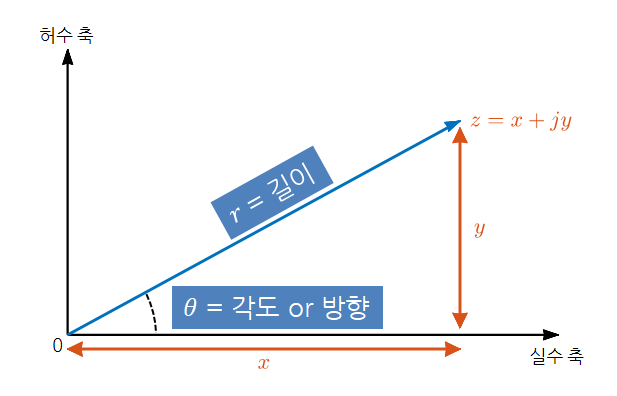
그림 5. 직각 좌표계와 극 좌표계의 관계
삼각비를 생각해본다면 $x$와 $y$의 좌표는 다음과 같이 표현할 수 있다.
\[\begin{cases} x = r\cos(\theta) \\ y = r\sin(\theta) \end{cases}\]즉, 극 좌표계의 $r$, $\theta$를 이용해 임의의 복소수 $z$ 를 다음과 같이 표현할 수 있다.
\[z=r\cos(\theta) + j r\sin(\theta)\]한편, 직교 좌표계에서 극좌표계로 표현을 수정하기 위해서는 원점으로부터 점까지의 길이와 각도를 계산하면 된다.
\[\begin{cases}r=\sqrt{x^2+y^2}\\\theta = \tan^{-1}(y/x)\end{cases}\]오일러 공식
원점으로부터의 거리가 1이고 실수축과의 각도가 $\theta$ rad인 복소수 $z$를 생각해보자.
\[z = \cos(\theta) + j \sin(\theta)\]위 식을 $\theta$에 대해 미분해보면 다음과 같은 결과를 얻을 수 있다.
\[\frac{dz}{d\theta}=-\sin(\theta) + j \cos(\theta)\]여기서 $j^2 = - 1$ 이므로,
\[\frac{dz}{d\theta}=j^2 \sin(\theta) + j\cos(\theta) = j(\cos(\theta) + j \sin(\theta)) = jz\]이고 양변을 $z$로 나눠
\[\frac{1}{z} \frac{dz}{d\theta} = j\]와 같이 바꿔 쓸 수 있다.
여기서 양변을 적분하면,
\[\int \frac{1}{z}dz = \int j d\theta\] \[\Rightarrow \ln(z)=j\theta + C\]와 같다.
($C$는 적분 상수)
(여기서 $\ln()$ 안의 $z$에 절대값을 씌우지 않은 것은 복소수의 길이는 항상 0보다 크기 때문이다.)
이제 $C$ 값을 확인해보자. $\theta=0$인 경우를 생각해보면,
\[\ln(z)=0+C=C\]그리고 $z$ 값은 본디 $z=\cos(\theta) + j\sin(\theta)$이므로,
\[z= \cos(0) + j\sin(0) = 1\]과 같다. 따라서, $\ln(z) = \ln(1) = 0 = C$와 같다.
따라서 적분 상수를 확인하였으므로,
\[\ln(z)=j\theta\]이고,
\[z=e^{j\theta}=\cos(\theta)+j\sin(\theta)\]이다.
결과로써 나온 수식만 떼어 놓고 보면 뭔가 기가막힌 것을 얻어냈다는 걸 알 수 있다.
\[e^{j\theta}=\cos(\theta) + j \sin(\theta)\]잘 보면 우변에 있는 것은 직교좌표계로 표현된 복소수 표현인데, 좌변에 있는 것은 $r$, $\theta$만을 이용해 표현된 복소수 값이 된다. (이 공식은 오일러 공식이라고도 불린다.) 즉, $r\angle\theta$와 같은 인위적인 표시 대신에 수학적으로 타당한 극좌표계 표현 방법을 복소 지수(complex exponential)를 이용해 표현할 수 있게 되는 것이다. 특히, 지수 함수(exponential function)을 이용하기 때문에 복소수 간의 곱셈, 나눗셈에 이용하면 계산이 아주 편리해지는 것을 예상할 수 있다.
복소수 사칙 연산과 시각화
복소수의 사칙 연산
복소수에 대한 사칙 연산은 $j^2=-1$ 인 것만 염두해둔다면 실수에서의 사칙연산과 크게 다르지 않다. $j$를 하나의 특별한 변수로 보는 것도 좋을 것 같다.
우선은 직교좌표형으로 쓴 복소수의 사칙연산을 확인해보자.
- 덧셈
- 뺄셈
- 곱셈
- 나눗셈
여기서 복소수 위의 $^*$ 표시는 complex conjugate(켤레 복소수) 연산이다.
- complex conjugate
위의 사칙연산 결과를 보면 곱셈과 나눗셈의 과정이 꽤 복잡하다는 것을 알 수 있다.
이에 대해 우리는 앞서 확인한 오일러 공식($e^{j\theta}=\cos(\theta)+j\sin(\theta)$)을 이용해 보자. 지수함수를 이용하기 때문에 곱셈과 나눗셈에 더 유리한 것을 알 수 있다.
- 오일러 공식 이용 곱셈
- 오일러 공식 이용 나눗셈
한편 complex conjugate은 각도의 부호만 바꾸어 계산할 수 있다.
- complex conjugate
복소수 사칙 연산의 시각화
복소수의 사칙 연산 중 덧셈과 뺄셈은 직교 좌표계의 2차원 벡터로 표현하는 것이 시각적으로 가장 이해하기 쉽다.
생각해보면 복소수의 실수부와 허수부는 각각 독립적으로 작용하기 때문에 기하학적으로 2차원 평면 상에 도시한 2차원 벡터와 기능은 완전히 동일하다.
복소수 덧셈의 경우는 벡터 합의 평행사변형 규칙을 생각하면 쉽게 생각해볼 수 있다.
혹은 더해지는 두 벡터 중 하나의 사본의 종점(end point)을 다른 한 벡터의 시점(starting point)에 둔 뒤, 합쳐진 벡터들의 양 끝을 연결시켜주면 두 벡터를 합한 결과를 얻을 수 있게 된다.
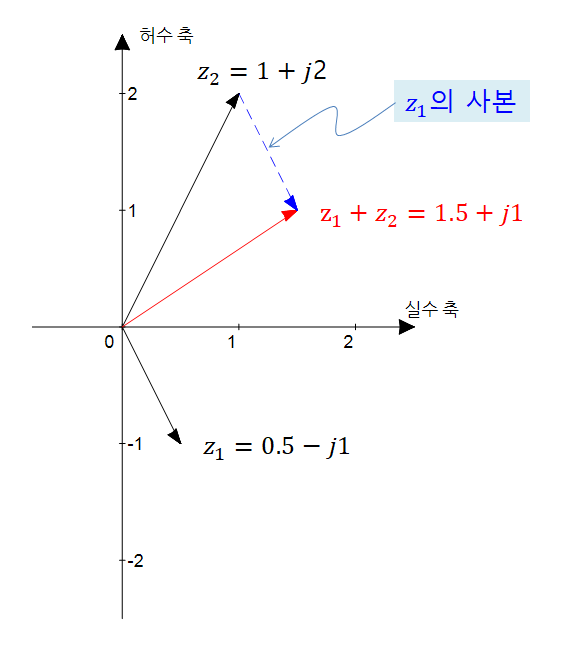
그림 6. 복소수 덧셈의 시각적 표현
뺄셈의 경우에는 $z_1-z_2$를 $z_1+(-z_2)$와 같이 생각하여 뺄셈을 당하는 벡터에 대해 반대방향으로 향하는 벡터를 상정한 뒤 더하면 된다.
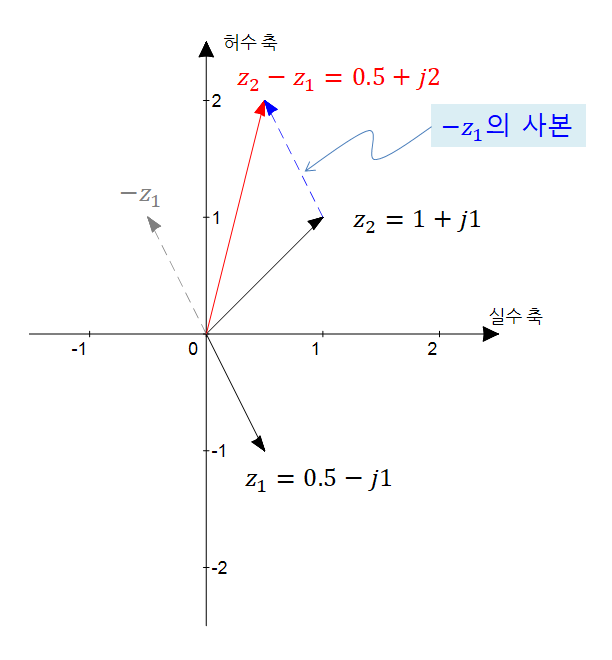
그림 7. 복소수 뺄셈의 시각적 표현
복소수 곱셈의 경우에는 극좌표계로 표현된 벡터를 생각하는 것이 좋다. 식 (28)을 보면 두 복소수를 곱해주면 두 복소수의 크기는 곱해지고 각도는 더해지는 것을 알 수 있다.
아래 그림에서 $\theta_3 = \theta_1+\theta_2$가 된다. 하지만 각도는 $-180°$에서 $180°$ 사이의 값으로 표현해주는 편이기 때문에 이 부분은 주의해서 360도의 배수를 더해주어 조정해주자.
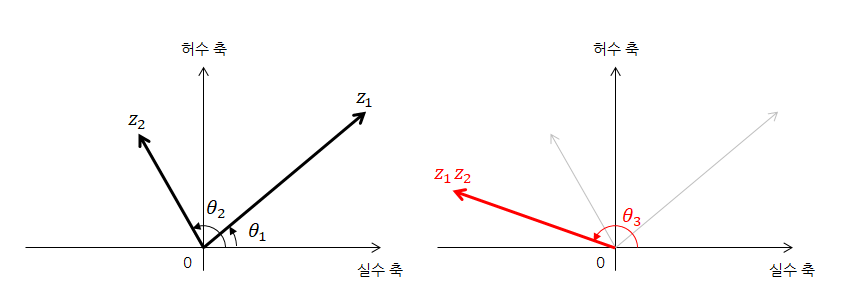
그림 8. 복소수 곱셈의 시각적 표현