중적분의 의미. 함수 아래에 있는 부피들을 잘게 쪼개서 더해주자.
※ 함수 곡면 아랫부분의 값만을 이용해 부피를 계산해주어 적분값보다는 추정 부피값이 작습니다.
정적분의 개념으로부터 출발
중적분의 개념은 여러가지 방식으로 이해할 수 있겠으나, 가장 시각적으로 이해하기 쉬운 넓이/부피의 계산에 관련된 내용으로부터 출발해보자.
고등학교 시절 구분구적법을 이용해 정적분의 개념을 익혔을 것이다.
그림 1은 구분구적법을 이용해 함수 곡선 아래의 넓이를 구해주는 과정을 보여주고 있다.
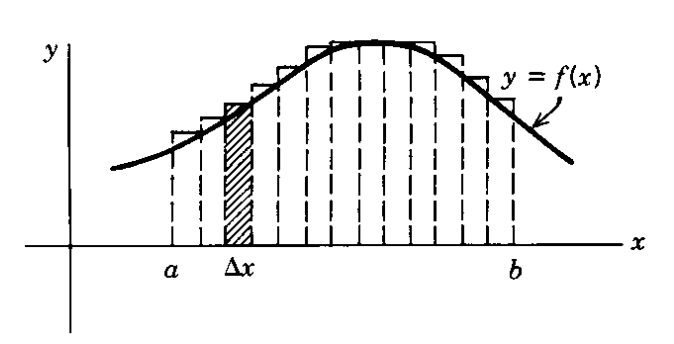
그림 1. 구분구적법을 이용해 함수 f(x) 아래의 넓이를 구해주는 과정을 통해 정적분의 개념을 얻었다.
그림 출처: 참고문헌 1의 Boas 공업수학 교재 / p.242의 Fig 2.1
함수가 $y = f(x)$라고 하면, $\Delta x$만큼의 길이를 곱해줘서 작은 사각형의 넓이를 생각해서 $a$부터 $b$까지 더해준다.
수식으로 쓰면 아래와 같이 구분구적법을 이용해 추정된 넓이의 값을 계산할 수 있다.
\[\sum_{x=a}^{b}f(x)\Delta x\]식 (1)에서 쪼개주는 작은 사각형의 밑변의 길이를 매우 작게하여 얻어진 수없이 많은 사각형의 넓이를 합하면 아래와 같이 좀 더 참값에 가까운 곡선 아래의 넓이를 계산할 수 있게 된다.
\[\Rightarrow \lim_{\Delta x \rightarrow 0}\sum_{x=a}^{b}f(x)\Delta x=\int_{a}^{b}f(x)dx\]여기서, 미적분의 기본정리를 이용하면
\[\frac{d}{dx}F(x) = f(x)\]이므로, 식 (2)의 적분값은 다음과 같이 계산할 수 있고 알려져 있다.
\[식(2) = F(b) - F(a)\]중적분의 개념으로 확장
정적분의 개념을 확장해서 중적분의 개념으로 확장해보자.
구분구적법을 이용하면 2차원 곡면아래의 부피를 계산할 수 있다.
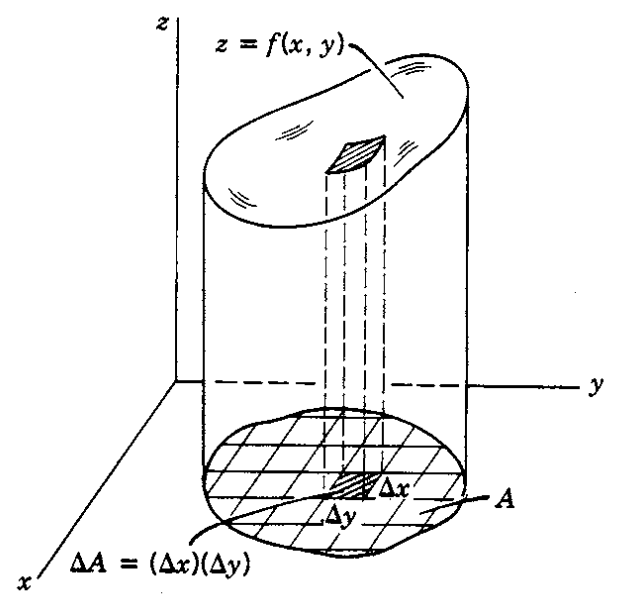
그림 2. 구분구적법을 이용해 함수 f(x, y) 아래의 부피를 구할 수 있다.
그림 출처: 참고문헌 1의 Boas 공업수학 교재 / p.242의 Fig 2.2
그림 2를 보면 3차원 데카르트 좌표 공간 상에 동그란 밑면을 가진 원통형 물체가 놓여있으며, 그 높이는 $z=f(x,y)$라는 함수로 주어져있다.
그림 1과 그림 2를 비교해보면, 정적분과 중적분의 여러가지 차이를 확인할 수 있는데, 우선 정적분에서 $\Delta x$로 주어졌던 미소길이는 중적분에서는 $\Delta A = \Delta x \Delta y$로 주어져있는 것을 알 수 있다.
또, 정적분에서 생각했던 ‘작은 사각형의 넓이’인 $f(x)\Delta x$는 중적분에서는 작은 나무 막대기의 부피인 $f(x,y)\Delta x \Delta y$로 개념이 확장된다.
표로 그 내용을 정리하면 다음과 같다.

표 1. 정적분과 중적분의 개념 비교
정적분에서 작은 사각형들의 넓이를 합쳤던 것 처럼 중적분에서는 작은 막대기의 부피를 합쳐볼 것이다.
육면체 막대기의 높이는 $밑면 \times 높이$로 계산할 수 있다. 이 경우 높이는 $f(x,y)$로 주어져있고 거기에 밑면의 넓이는 $\Delta x \Delta y$로 주어져 있기 때문에 다음과 같이 작은 막대기의 부피를 생각해볼 수 있다.
\[f(x,y)\Delta x\Delta y\]그런 다음, 정적분 계산을 할 때 주어진 $a$에서 $b$까지의 범위에 대해 작은 사각형의 넓이를 더해준 것 처럼, 중적분에서는 주어진 적절한 $x$와 $y$의 위치에 대해 작은 막대기들의 부피를 다 더해주도록 하자.
\[\sum_x\sum_y f(x,y)\Delta x \Delta y\]그런 다음, 정적분에서와 마찬가지로 극한의 개념을 이용해 다음과 같이 부피값을 수렴시켜줄 수 있다.
\[\lim_{\Delta x \rightarrow 0}\lim_{\Delta y \rightarrow 0}\sum_x\sum_y f(x,y)\Delta x \Delta y = \iint_Af(x,y)dxdy\]중적분에서 적절한 x, y의 위치란?
그림 1에서 정적분에서는 $x=a$에서 $x=b$까지 변했다.
그런데, 그림 2에서 볼 수 있듯이 중적분과 같이 밑면의 모양이 단순하지 않은 경우 $x$와 $y$의 범위를 어떻게 정해야 할까?
\[\iint_Af(x,y)dxdy = \int_{x=?}^{?}\int_{y=?}^{?}f(x,y)dxdy\]그림 3과 같이 기둥의 밑면을 x축으로 정사영시켰다고 생각해보자. 그렇게 했을 때 결정되는 가장 양 끝에 있는 값들을 각각 $x=a$, $x=b$라고 하자.
또, 밑면의 가장자리를 x축과 수평한 선을 따라 절반으로 나누고 한쪽을 $y_1(x)$, $y_2(x)$라고 각각 이름 붙이자.
글로 설명한 것을 아래 그림을 참고해 이해해보도록 하자.
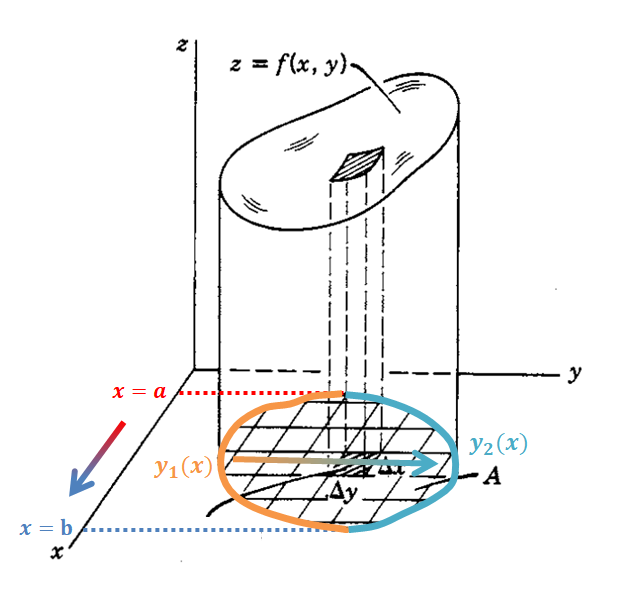
그림 3. xy 평면상에 있는 임의의 형태의 밑면에 대해 x, y의 범위를 결정하는 방법
그림 출처: 참고문헌 1의 Boas 공업수학 교재 / p.242의 Fig 2.2
정적분에서는 우리가 $x$는 $a$에서 $b$까지 바꿔가면서 합을 계산했다고 하면,
중적분에서는 $x$는 $a$에서 $b$까지 쌓여가고, $y$는 $y_1(x)$에서 $y_2(x)$까지 쌓여간다고 생각하면 위 식 (8)의 $x$와 $y$의 적분 범위를 결정할 수 있게 된다.
\[\iint_Af(x,y)dxdy = \int_{x=a}^{b}\int_{y=y_1(x)}^{y_2(x)}f(x,y)dxdy\]이렇게 구성된 식을 더 풀어 생각해보면 $y$에 대한 식이 모두 $x$에 대한 함수로 결정되어 있기 때문에 결국 $x$에 대한 적분으로 바뀌게 되어 중적분을 정적분 계산하듯이 풀어낼 수 있게 된다.
중적분 문제 예시
이번에는 실제로 중적분을 계산할 수 있도록 예제 문제를 하나 풀어보도록 하자.
아래 그림 4에서 처럼 평면 $z=1+y$과 $xz$ 평면, $yz$ 평면, $2x+y=2$ 평면으로 둘러싸인 고형물의 부피를 계산해보자.
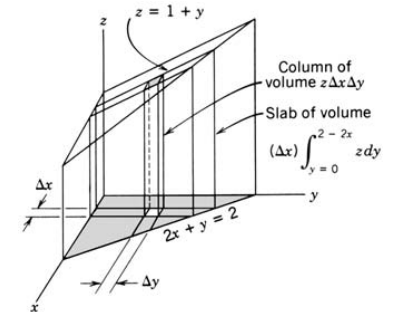
그림 4. 중적분 계산 예제
그림 출처: 참고문헌 1의 Boas 공업수학 교재 / p.243의 Fig 2.3
위에서 구분구적법을 이용해 설명한 것 처럼 중적분 값을 한마디로 적으면 아래 식과 같을 것이다.
\[\iint_A z dydx = \iint_A (1+y)dy dx\]여기서 이중적분 기호 아래 $A$라고 표현한 것은 그림 4에 회색으로 칠해진 삼각형을 밑면으로하여 이중적분을 수행해주자는 의미이다.
그림 4에서 밑면의 삼각형은 x, y 좌표축과 $2x+y=2$라는 평면으로 구성되어 있으므로, $x$가 쌓이는 범위는 $[0, 1]$이라고 할 수 있으며,
$y$ 축 방향으로 쌓일 때는 $y$ 값이 가장 작을 때는 $y=0$이며, 가장 클 때는 $y=2-2x$라는 것을 알 수 있다.
따라서, 식 (10)은 다음과 같이 쓸 수 있다.
\[\int_{x=0}^{x=1}\int_{y=0}^{y=2-2x}{(1+y)dydx}\]이중적분 중 내부에 있는 $y$에 대한 적분을 먼저 전개하면,
\[\Rightarrow \int_{x=0}^{x=1}\left|y+\frac{1}{2}y^2\right|_{y=0}^{y=2-2x}dx\] \[=\int_{x=0}^{x=1}2-2x+\frac{1}{2}(2-2x)^2dx\] \[=\int_{x=0}^{x=1}4-6x+2x^2dx\]이제 $x$에 대해 정적분 값을 계산해주자.
\[\Rightarrow \left|4x-3x^2+\frac{2}{3}x^3\right|_{0}^{1}\] \[=4-3+\frac{2}{3} =\frac{5}{3}\]즉, 구해주고자하는 고형물의 부피는 5/3이라는 것을 이중적분을 통해서 계산할 수 있다.
참고 문헌
본 article에서 사용된 그림은 아래의 참고 문헌 1에서 가져왔습니다.
- Mathematical Methods in the Physical Sciences / Mary L. Boas / 3e