마르코프 부등식 (Markov Inequality)

마르코프 부등식은 음수가 아닌 랜덤 변수에 대해 성립하는 부등식이다. 마르코프 부등식의 정의부터 보면 다음과 같다.

$X$가 음수가 아닌 값을 가지는 랜덤 변수라고 했을때, $\alpha\gt 0$¹를 만족하는 임의의 상수 $\alpha$에 다음이 성립한다.

\[P(X\geq \alpha) \leq E[X]/\alpha\]

위 식의 의미를 간단히 살펴보기 위해 아래의 그림을 보도록 하자.

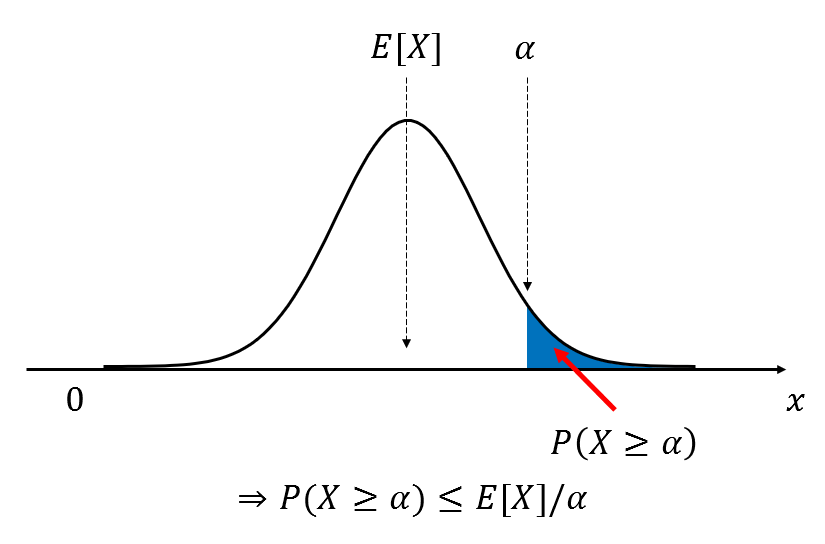
그림 1. 마르코프 부등식이 의미하는 것은 전체 데이터 분포에서 기댓값을 기준으로 랜덤변수 $x$가 어떤 극값 $\alpha$ 보다 클 확률에 관한 것이다.

그림 1을 보면 어떤 랜덤 변수 $X$에 대한 pdf가 그려져 있는 것을 알 수 있다. 여기서 $X$는 음수가 아닌 값이라는 점을 강조하고자 가로축 왼쪽에 0을 표시했다. 또, 기댓값은 임의로 분포 중앙으로 설정하였으며 $P(X\geq \alpha)$는 파란색 영역으로 표시되어 있다.

정리하자면 마르코프 부등식은 음수가 아닌 랜덤 변수에 대해 기댓값을 기준으로 $X$가 극값 $\alpha$ 보다 클 확률에 관한 정리(theorem)라고 할 수 있다.

증명은 아주 간단하다. $X$에 관한 pdf가 $f_X(x)$라고 하면 이의 기댓값은 다음과 같다.

\[E[X]=\int_x x f_X(x)dx\]

위 적분에 대한 적분 범위를 $\alpha$를 기준으로 나눠 다음과 같이 쓸 수 있다.

\[\Rightarrow \int_{0\leq x \lt \alpha}xf_X(x)dx + \int_{X\geq \alpha}xf_X(x)dx\]

여기서 $x$의 값은 항상 음수가 아닌 값이므로 위 식의 왼쪽 항은 항상 양수이다. 따라서, 아래와 같은 관계가 성립한다.

\[\Rightarrow \int_{0\leq x \lt \alpha}xf_X(x)dx + \int_{X\geq \alpha}xf_X(x)dx \geq \int_{X\geq \alpha}xf_X(x)dx\]

또한, 위 식의 우변의 값에서 $X\geq \alpha$이므로 다음이 성립한다.

\[\Rightarrow \int_{X\geq \alpha}xf_X(x)dx\geq \int_{X\geq \alpha}\alpha f_X(x)dx % 식 (5)\]

따라서, 결론적으로 식 (2)와 식 (5)만을 가져오면,

\[\Rightarrow E[X]\geq \int_{x\geq \alpha} \alpha f_X(x)dx % 식 (6)\]

이며, pdf와 확률의 정의에 따라 위 식은 다음과 같이 쓸 수도 있다.

\[식(6)\Rightarrow E[x]\geq \alpha P(X\geq \alpha) % 식 (7)\]

여기서 위 식을 정리하면 식 (1)을 얻을 수 있다.

체비셰프 부등식 (Chebyshev Inequality)

체비셰프 부등식 유도

체비셰프 부등식은 다음과 같다. 임의의 랜덤 변수 $X$와 임의의 상수 $\alpha$에 대하여 다음이 성립한다.

\[P(\left|X-E[X]\right|\geq\alpha)\leq Var[X]/\alpha^2 % 식 (8)\]

체비셰프 부등식은 마르코프 부등식과 다르게 $X$와 $\alpha$에 대한 제약 조건이 없으나 절대값 부호에서 볼 수 있듯이 양측 극값 $E[X]\pm\alpha$에 대한 부등식이다.

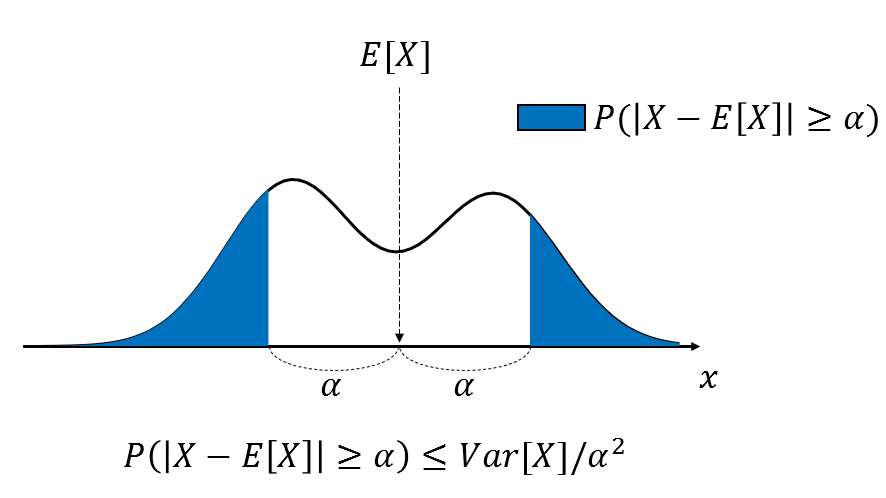
그림 2. 체비셰프 부등식이 의미하는 것은 전체 데이터 분포에서 기댓값을 기준으로 랜덤변수 $x$가 어떤 양쪽 극값 $E[X]\pm\alpha$ 보다 크거나 작은 확률에 관한 것이다.

증명은 생각보다 간단하고 위의 마르코프 부등식을 이용하여 진행된다. 식 (8)의 부등식 $|X-E[X]|\gt\alpha$은 다음과 같이 생각할 수 있다.

\[|X-E[X]|\geq\alpha \Leftrightarrow (X-E[X])^2\geq \alpha^2\]

이에 아래와 같은 새로운 랜덤 변수 $Y$를 정의하자.

\[Y=(X-E[X])^2\]

그러면 분산의 정의 상 $E[Y]=Var[X]$이다. 따라서, $Y$와 $\alpha^2$에 대한 마르코프 부등식을 확인하면 다음과 같다.

\[P(Y\gt\alpha^2)\leq E[Y]/\alpha^2\]

이를 $X$에 대한 식으로 다시 바꾸면,

\[P((X-E[X])^2\geq\alpha^2)\leq Var[X]/\alpha^2 % 식 (12)\]

가 되고 식 (9)에 의해 식 (8)을 얻을 수 있게 된다.

체비셰프 부등식의 의의

식 (8)에서 $\alpha$ 대신에 $k\sigma$를 대입해보자. 여기서 $\sigma$는 표준편차를 의미한다. 그러면 아래와 같은 식으로 변형할 수 있다.

\[식(8) \Rightarrow P(\left|X-E[X]\right|\geq k\sigma)\leq Var[X]/{k^2\sigma^2} % 식 (13)\] \[\Rightarrow P(\left|X-E[X]\right|\geq k\sigma)\leq \frac{1}{k^2} % 식 (14)\]

우리가 식 (14)를 통해서 얻을 수 있는 인사이트는 무엇일까? 바로, 임의의 확률 분포에 대해 평균과 분산을 통해 얻을 수 있는 정보에 관한 것이라고 할 수 있다. 다시 말하면, 어떤 분포라도 거의 대부분의 데이터들은 평균에 가깝게 붙어있다는 의미이며, 표준 편차를 기준으로 얼마만큼 떨어져있는지를 알려주는 것이다.

가령, $k=2$일 때를 생각해보면, 식 (14)는 확률 변수 $X$의 분포는 기댓값 $E[X]$를 중심으로 $\pm 2$ 표준편차 밖에 놓인 데이터가 1/4, 즉 25% 라는 것을 말해주고 있다. 다른 말로 하면 평균을 중심으로 $\pm$ 2 표준편차 안에 75%의 데이터가 들어있다는 것을 의미한다. (참고로 정규분포라면 $\pm$ 2 표준편차 안에 95%의 데이터가 들어오게 된다. 체비셰프 부등식은 어떤 모양의 분포라도 성립하는 “느슨한” 조건을 갖는 부등식이라는 점에 주목하자.)

일반적으로, 체비셰프 부등식이 말해주는 것은 데이터들 중 평균값으로부터 $k$ 표준편차 이상 떨어진 것들은 $1/k^2$ 이상 차지하지 않는다는 것을 의미한다.

아마, 이런 이유로 통계학자들은 확률 분포에 관한 가장 유용한 대푯값들로 평균 & 표준편차를 사용하는 것일 수 있겠다. 평균과 표준편차만 제시되어 있다면 데이터 전체의 분포를 확인하지 않고도

“대략적으로 평균 $\pm$ 2 표준편차 안에 대부분의 데이터가 들어오긴 하겠군.”

하고 생각할 수 있기 때문이다.

Reference

• Outlier Analysis 2nd e.d., Charu C. Aggarwal, Springer
• 빅데이터를 지배하는 통계의 힘 (실무활용 편), 니시우치 히로무, 비전코리아