Prerequisites
본 포스트를 잘 이해하기 위해서는 다음의 내용에 대해 알고 오시는 것이 좋습니다.
치환행렬의 고윳값, 고유벡터
순환행렬의 고윳값, 고유벡터는 치환행렬의 고윳값, 고유벡터와 밀접한 관련이 있다.
따라서, 우리는 치환행렬의 고윳값, 고유벡터를 먼저 계산해보도록 하자.
우리가 사용하는 치환행렬은 치환행렬은 순환행렬과 컨볼루션 편에서 보았던 것과 마찬가지로 아래와 같이 cyclic permutation을 수행해주는 행렬이다.
\[P = \begin{bmatrix} 0 & 0 & \cdots & 0 & 1 \\ 1 & 0 &\cdots & 0 & 0 \\ 0 & \ddots &\ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & 0 \\ 0 & \cdots & 0 & 1 & 0 \end{bmatrix}\]일반적인 $n\times n$ 크기의 행렬 $P$에 대해서 고윳값, 고유벡터를 구하는 것은 어려울 수 있기 때문에 $4\times 4$ 크기의 치환 행렬 $P_4$의 고윳값, 고유벡터를 계산해보자.
먼저 $P_4$의 고윳값을 계산하기 위해 특성방정식을 써보면 다음과 같을 것이다.
\[det(P_4-\lambda I) = 0\] \[\Rightarrow det\left(\begin{bmatrix}0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0\end{bmatrix}-\lambda I\right)=0\] \[\Rightarrow det\left(\begin{bmatrix}-\lambda & 0 & 0 & 1 \\ 1 & -\lambda & 0 & 0 \\ 0 & 1 & -\lambda & 0 \\ 0 & 0 & 1 & -\lambda\end{bmatrix}\right)=0\]$3\times 3$ 크기 이상의 행렬식은 수반행렬을 이용해 계산할 수 있다.
즉,
\[\Rightarrow 1\times (-\lambda)\times det\left(\begin{bmatrix}-\lambda & 0 & 0 \\ 0 & -\lambda & 0 \\ 0 & 0 & -\lambda \end{bmatrix}\right)-1\times(1)\times det\left(\begin{bmatrix} 1 & -\lambda & 0 \\ 0 & 1 & -\lambda \\ 0 & 0 & 1 \end{bmatrix}\right) = 0\] \[\Rightarrow \lambda^4 - 1 = 0\]따라서, $P_4$의 고윳값은 $\lambda = 1, -1, i, -i$이다.
이를 이용해 고유벡터를 계산해보자.
1) $\lambda = 1$인 경우
$P_4v=\lambda v$를 만족해야 하므로,
\[(P_4-\lambda I)v = (P_4-I)v = 0\]이고, $v = [v_1, v_2, v_3, v_4]^T$라 했을 때
\[\begin{bmatrix} -1 & 0 & 0 & 1 \\ 1 & -1 & 0 & 0 \\ 0 & 1 & -1& 0 \\ 0 & 0 & 1 & -1\end{bmatrix}\begin{bmatrix}v_1\\v_2\\v_3\\v_4\end{bmatrix} = 0\]이어야 하므로,
$v_1=v_4$, $v_1 = v_2$, $v_2=v_3$, $v_3 = v_4$의 관계를 만족하는 고유벡터 $v$는
\[v=\begin{bmatrix}1\\1\\1\\1\end{bmatrix}\]이다.
2) $\lambda = -1$인 경우
$\lambda = 1$인 경우와 유사한 방법을 통해 생각하면,
\[\begin{bmatrix} 1 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 1& 0 \\ 0 & 0 & 1 & 1\end{bmatrix}\begin{bmatrix}v_1\\v_2\\v_3\\v_4\end{bmatrix} = 0\]을 만족하는 고유벡터는
$v_1=-v_4$, $v_1 = -v_2$, $v_2=-v_3$, $v_3 = -v_4$의 관계를 만족하는 고유벡터 $v$는
\[v=\begin{bmatrix}1\\-1\\1\\-1\end{bmatrix}\]3) $\lambda = i$인 경우
이 경우의 고유벡터는 위의 두 가지 방법과 유사한 방법을 통해
\[v = \begin{bmatrix}1 \\ i \\ i^2 \\ i^3 \end{bmatrix}\]임을 알 수 있다.
4) $\lambda = -i$인 경우
이 경우의 고유벡터는 위의 두 가지 방법과 유사한 방법을 통해
\[v = \begin{bmatrix}1 \\ (-i) \\ (-i)^2 \\ (-i)^3 \end{bmatrix}\]임을 알 수 있다.
일반적으로 $n\times n$ 크기의 치환행렬의 고윳값은 $\lambda^n-1=0$을 만족하는 $\lambda$라고 할 수 있는데, 이 값을 일반적으로 쓰자면 다음과 같다1.
\[\lambda_k = \exp\left(-j\frac{2\pi}{n}k\right)\text{ for } k = 0, 1, \cdots ,n-1\]그리고 각 고윳값에 대응되는 고유벡터는 다음과 같다.
\[v_k = \begin{bmatrix}(\lambda_k)^0 \\ (\lambda_k)^1\\ \vdots \\ (\lambda_k)^{n-1}\end{bmatrix}\text{ for } k = 0, 1, \cdots ,n-1\]순환행렬의 고유벡터
\[C= \begin{bmatrix} x_0 & x_{n-1} & \cdots & x_2 & x_1 \\ x_1 & x_1 &\cdots & x_3 & x_2 \\ x_2 & \ddots &\ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & x_0 & x_{n-1} \\ x_{n-1} & \cdots & x_2 & x_1 & x_0 \end{bmatrix} = \left(\sum_{i=0}^{n-1}x_i P^{i}\right)\]순환 행렬의 고유벡터는 치환 행렬의 고유벡터와 같다.
$P$의 고윳값 $\lambda$와, 고유벡터 $v$는 다음의 식을 만족한다.
\[Pv=\lambda v\]순환행렬 $C$의 고유벡터를 마찬가지로 $v$라고 하면 순환행렬의 고윳값 $\xi$에 대해 다음의 식을 만족해야 한다.
\[Cv=\xi v\]순환행렬과 치환행렬의 관계에 따라 위 식은 다음과 같이 쓸 수 있다.
\[Cv = x_0 I v + x_1 P^1 v + \cdots + x_{n-1}P^{n-1}v\] \[=x_0 \lambda^0 v + x_1 \lambda^1 v + \cdots + x_{n-1}\lambda^{n-1}v\] \[=\left(\sum_{i=0}^{n-1}x_i\lambda^i\right)v = \xi v\]즉, 순환행렬의 고유벡터와 치환행렬의 고유벡터는 같다.
기저의 변환에 기반한 푸리에 행렬의 이해
벡터를 표현하는 ‘기저’에 대해 생각해보도록 하자.
벡터의 기본 연산 편에서는 벡터의 특성에 대해 잠깐 언급한 적이 있었다.
그 중 처음 두 가지는 ‘벡터란 화살표 같은 것’이라는 점과 ‘벡터란 숫자를 순서대로 나열한 것’이었다.
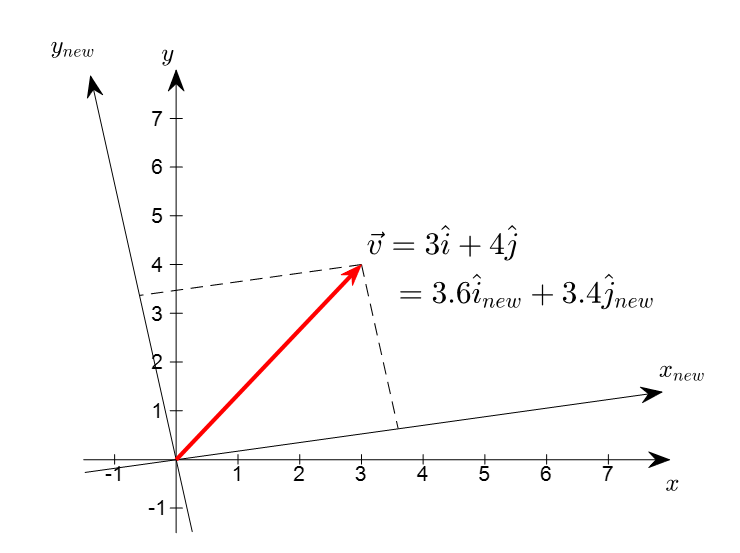
그림 1. 좌표계의 변화에 대해 불변하는 벡터의 기하학적 특성
그림 1을 통해서 알 수 있는 것은 하나의 벡터를 표현하기 위해 전혀 다른 좌표계를 이용해서 표현할 수 있다는 것이다.
또, 어떤 좌표계를 이용하면 벡터를 표현하는 숫자의 나열들이 간결한데 비해, 또 어떤 좌표계를 선택하면 숫자의 나열들이 복잡해진다.
그래서 우리는 적절한 좌표계를 선정함으로써 쉽게 데이터(즉, 벡터)를 다룰 수 있다.
여기서 말하는 ‘좌표계’의 기본 단위가 ‘기저(basis)’라고 말 할 수 있는데, 다시 말하자면, 우리의 목적에 맞는 기저를 선택하면 같은 벡터(즉, 주어진 데이터)를 좀 더 쉽거나 유용하게 표현할 수 있다.
우리가 일반적으로 사용해오던 기저는 standard basis라고 할 수 있다. 가령, 아래와 같은 벡터 $\vec{x}$에 대해서,
\[\vec{x} = \begin{bmatrix}x_0\\x_1\\ \vdots \\ x_{n-1}\end{bmatrix}\]standard basis를 사용한다는 것은 아래와 같이 1 하나와 나머지는 0으로 채워진 기저벡터를 이용해 벡터 $\vec{x}$를 표현한 것이라고 할 수 있다.
\[\begin{bmatrix}x_0\\x_1\\ \vdots \\ x_{n-1}\end{bmatrix} = x_0 \begin{bmatrix}1\\0\\ \vdots \\ 0\end{bmatrix} + x_1 \begin{bmatrix}0\\1\\ \vdots \\ 0\end{bmatrix} + \cdots + x_{n-1} \begin{bmatrix}0\\0\\ \vdots \\ 1\end{bmatrix}\]한편, 지금까지 확인한 내용에 따르면 어떤 벡터든 circulant matrix $C$와 $\delta$ 벡터의 곱으로 생각할 수 있는데, 이 말은 다시 말해 어떤 신호던지 $\delta$벡터가 변환되어서 얻어진 결과로 지금의 데이터를 볼 수 있다는 말이기도 하다.
\[\vec{x} = C\delta=\left(\sum_{i=0}^{n-1}x_i P^{i}\right)\delta\](작성 중입니다…)
-
아래의 Lambda의 exponential 안의 부호는 ‘+’ 나 ‘-‘ 모두 관계없으나 뒤에서 서술할 푸리에 행렬과의 관계를 고려해 부호를 ‘-‘로 설정하였음. ↩