※ 본 포스팅의 내용은 Thomas Judson의 The ordinary differential equations project에서 많은 부분을 차용하였음을 밝힙니다.

지난 변수분리법 포스팅에서는 가장 단순한 1계 선형 미분방정식의 형태인 변수분리형 미분방정식에 대해 풀어보았다.

이번 시간에는 변수분리법으로는 풀 수 없는 조금 더 일반적인 형태의 1계 선형 미분 방정식의 해법에 대해 알아보고자 한다.

우리가 풀고자하는 미분방정식의 형태는 다음과 같다.

\[\frac{dx}{dt}+p(t)x=q(t) % 식 (1)\]

위의 식 (1)이 변수분리법에서 본 식과 다른 점은 가운데 있는 $p(t)$가 더 이상 상수가 아니라는 점이다.

만약 $p(t)$가 $t$에 관한 식이 아니라면 변수분리법으로 문제를 해결할 수 있을 것이다.

‘선형(linear)’의 의미

미분방정식을 공부할 때 간간히 선형 미분방정식이란 얘기를 듣게 된다.

추후에 우리는 미분이라는 계산이 ‘선형 연산자’라는 얘기를 종종 듣게 될 것이다.

이 내용에 대해서는 한참 뒤에 Sturm-Liouville 문제를 소개할 때 더 자세하게 다루게 되겠지만, 이번에는 간단하게 선형의 의미에 대해서만 알고 넘어가보도록 하자.

---

우리는 우선 연산자(operator)라는 개념에 대해서 먼저 짚고 넘어가야 한다.

미분방정식을 공부할 때 생각하는 ‘연산자’란 어떤 함수에 작용해 그 함수를 다른 함수로 변형시켜주는 함수를 의미한다.

어떻게 생각하면 함수에 작용해 변형된 함수를 얻는 ‘행위자’라고 할 수 있다.

다시 말해 식 (1)을 이렇게 생각해볼 수 있다. 임의의 연산자 $O(\cdot)$을 생각해보자. 이 연산자는 $x(t)$라는 함수에 대해 작용하면 다음과 같은 출력을 내어준다.

\[x(t)\rightarrow O(\cdot) \rightarrow \frac{dx}{dt}+p(t)x % 식 (2)\]

그리고 이 연산자가 ‘선형’ 연산자라면 다음과 같은 성질을 만족해야 한다.

임의의 상수 $c$에 대해,

\[O(c\cdot x(t))=c\cdot O(x(t)) % 식 (3)\]

또, 서로 독립적인 함수 $x_1(t)$와 $x_2(t)$에 대해,

\[O(x_1(t) + x_2(t)) = O(x_1(t)) + O(x_2(t)) % 식 (4)\]

따라서, 연산자 $O(\cdot)$가 선형연산자라면 다음과 같은 결과가 도출될 수 있다.

임의의 상수 $c_1$과 $c_2$에 대해서,

\[O(c_1 x_1(t) + c_2 x_2(t)) = c_1 O(x_1(t)) + c_2 O(x_2(t)) % 식 (5)\]

이다¹.

다시, 미분방정식이 선형이라는 것의 의미는 식 (2)와 같은 연산자가 선형 연산자임을 말하는 것이다. 즉, 서로 독립적인 함수 $x_1(t)$와 $x_2(t)$에 대해서,

\[\frac{d}{dt}\left(c_1x_1(t) + c_2x_2(t)\right)+p(t)\left(c_1x_1(t) + c_2x_2(t)\right) % 식 (6)\] \[=c_1\frac{dx_1}{dt}+c_1p(t)x_1(t) + c_2\frac{dx_2}{dt}+c_2p(t)x_2(t) % 식 (7)\]

와 같이 쓸 수 있다는 의미에서 ‘선형 미분방정식’이라는 이름이 붙는 것이다.

비선형 미분방정식의 예시

미분 연산자가 비선형인 경우에 대해서도 예시를 들어 확인해보자면 아래와 같은 미분방정식은 비선형 미분방정식이다.

\[\frac{dx}{dt}+x^2 = 0\]

왜냐면 아래와 같이 두 식이 일치하지 않기 때문이다.

\[O(c_1 x_1 + c_2 x_2 ) = c_1 \frac{dx_1}{dt}+c_1^2 x_1^2 + c_2 \frac{dx_2}{dt}+c_2^2x_2^2+2c_1x_1c_2x_2\] \[\neq c_1O(x_1)+c_2O(x_2) = c_1 \frac{dx_1}{dt}+c_1x_1^2+c_2\frac{dx_2}{dt}+c_2 x_2^2\]

1계 선형 미분 방정식의 해법

식 (1)과 같은 형태의 미분 방정식을 풀기 위해선 미분의 연쇄법칙(chain rule)을 이용해야 한다.

식 (1)의 가운데에 있는 $p(t)$에 대해서, $\mu’(t) = p(t)$ 혹은 $\int p(t) dt = \mu(t)$와 같은 관계를 갖는 $\mu(t)$를 생각해보자.

그러면 $e^{\mu(t)}x$의 $t$에 대한 미분은 다음과 같이 쓸 수 있다는 것을 알 수 있다.

\[\frac{d}{dt}\left(e^{\mu(t)}x(t)\right)=e^{\mu(t)}\mu'(t)x(t) + e^{\mu(t)}x'(t) % 식 (11)\] \[=e^{\mu(t)}\left\lbrace \mu'(t)x(t)+x'(t)\right\rbrace % 식(12)\] \[=e^{\mu(t)}\left\lbrace p(t)x(t) + x'(t)\right\rbrace % 식(13)\]

식 (13)의 중괄호 안에 있는 식은 결국 식 (1)의 좌변과 같은 것이다. 따라서,

\[식(11)\Rightarrow \frac{d}{dt}\left(e^{\mu(t)}x(t)\right) = e^{\mu(t)}q(t)\] \[\therefore e^{\mu(t)}x(t)=\int e^{\mu(t)}q(t)dt + C\]

즉,

\[x(t) = \frac{1}{e^{\mu(t)}}\left(\int e^{\mu(t)}q(t)dt + C\right)\]

와 같이 풀어지는 것을 알 수 있다.

여기서 중요한 포인트 중 하나는 $x$에 $e^{\mu(t)}$를 곱해주는 과정에서 이 해법이 시작된다는 점인데, $e^{\mu(t)}$를 적분 인자(integrating factor)라고 한다.

예시 문제

미분방정식은 이 해법이 어떻게 작동하는지 알아보는 것이 중요하기 때문에 실제로 문제를 많이 풀어보는 것이 중요할 것이다.

소금물 채워넣기 문제

이전 변수분리법 포스팅에서 본 문제를 살짝 업그레이드 해서 소금물 채워넣기 문제를 풀어보자.

이전 변수분리법 포스팅에서와는 달리 이번에는 물의 수위가 계속 올라갈 수 있게 문제를 수정할 것이다.

물탱크에 소금물을 집어넣어서 물탱크에 들어있는 물의 염도가 상승할 수 있게 만든다고 하자.

가령, 물탱크의 총 부피는 1000 리터인데, 500 리터의 맹물이 들어있고, 0.5kg/L 농도의 소금물을 계속해서 넣어주기 시작한다고 하자.

이 때, 1분에 10L의 0.5kg/L 농도의 소금물이 계속해서 들어가게 된다고 하자.

물탱크의 소금물은 균일하게 섞일 수 있도록 물탱크의 물을 계속 저어주고 있다고 가정하겠다.

그런데, 물탱크의 바닥에 물이 새고 있다고 하자. 물이 새는 속도는 1분당 9L라고 해보겠다.

이런 경우 시간에 따른 소금물의 농도는 어떻게 변하게 될까?

---

이 문제는 미분방정식을 이용해야 하는 문제이고, 1계 선형미분방정식을 이용해야 한다.

물탱크 안의 소금의 양을 $x(t)$라고 해보자. 그러면, 물탱크 안의 소금양의 시간에 따른 변화율은 $dx/dt$ 일 것이다.

또, 소금의 시간 당 변화율은 들어오는 소금의 비율과 나가는 소금의 비율의 차이이므로,

\[\frac{dx}{dt}=\text{rate in } - \text{rate out} % 식 (17)\]

이라고 쓸 수 있다.

들어오는 소금물은 10L인데, 그중 5kg이 소금이므로 1분당 5kg의 소금이 들어오는 셈이다. 즉,

\[\text{rate in}=5\]

이다.

한편, 물탱크 안에 들어있는 소금물의 부피 $V(t)$는 처음에는 500 리터였다가 10L의 물이 들어오고 9L의 물이 나가므로 매 1분마다 1L씩 늘어난다. 따라서 $V(t) = 500 + t$이라고 할 수 있다.

따라서, 나가는 소금의 양은 현재 물탱크 안의 소금 양 $x$에 비례하고 현재 물탱크 안의 물 부피 $V(t)$에 반비례 할 것이다. 즉,

\[\text{rate out}=\frac{9}{500+t}x\]

이다.

따라서,

\[\frac{dx}{dt}=5-\frac{9}{500+t}x % 식 (20)\]

와 같이 미분방정식을 세워줄 수 있다.

위 식을 다시 살짝 정리하면,

\[\Rightarrow \frac{dx}{dt}+\frac{9}{500+t}x=5 % 식 (21)\]

과 같은데, 양변에 곱할 적분 인자 $e^{\mu(t)}$를 계산해보면 다음과 같다.

\[e^{\mu(t)}=\exp\left(\int \frac{9}{500+t}dt\right)=e^{9\ln(500+t)}=(500+t)^9\]

따라서, 식 (21)의 양변에 적분인자 $e^{\mu(t)}$를 곱해주면,

\[\Rightarrow (500+t)^9\frac{dx}{dt}+9(500+t)^8x=5(500+t)^9\] \[\Rightarrow \frac{d}{dt}\left[(500+t)^9x\right]=5(500+t)^9\]

양변을 적분해주면,

\[(500+t)^9x=\frac{5}{10}(500+t)^{10}+C\] \[\therefore x(t) = \frac{1}{2}(500+t)+\frac{C}{(500+t)^9}\]

이다.

처음에 물탱크에 들어있는 물은 소금이 하나도 들어있지 않은 맹물이었으므로,

\[x(0) = \frac{1}{2}(500+0)+\frac{C}{(500+0)^9}=250+\frac{C}{500^9}=0\]

따라서,

\[C = -250 * 500^9=-\frac{1}{2}\times 500^{10}\]

임을 알 수 있다.

물탱크의 물은 500분 후에 가득채워질텐데 이 때 까지의 소금양에 관한 그래프를 그려보면 다음과 같을 것이다.

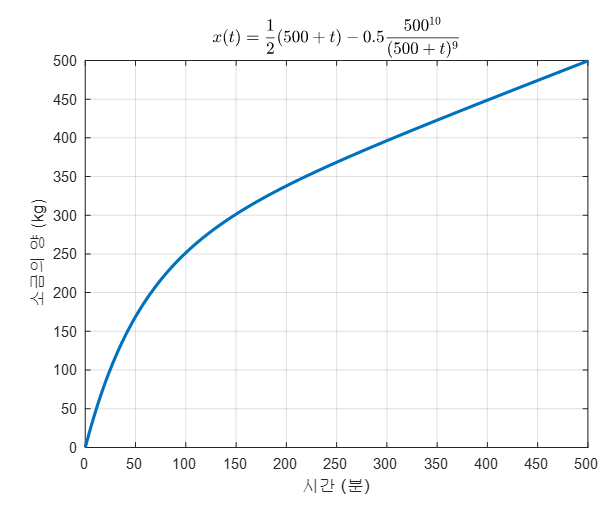
그림 1. 물이 새는 물탱크에 소금물을 서서히 채워넣어 줄 때 물탱크 내의 소금양의 변화

해의 존재성과 유일성

미분방정식을 풀 때는 해의 존재성과 유일성에 대한 보장을 받음으로써 어떤 방식으로 해를 구하던지 상관없이 해를 잘 구하기만 했다면,

그것으로 충분하다는 것을 인지하는 것이 미분방정식을 공부할 때 도움이 된다.

(다시 말하면, 왜 내가 굳이 남이 생각해둔 이런 솔루션 획득 방법을 알아야할까?라는 질문에 답이 될 수 있다는 것이다.)

1계 선형미분방정식은 거의 대부분의 경우 해의 존재성과 유일성을 보장받을 수 있다. 구체적으로는 아래와 같은 조건에서 그러하다.

\[y'+p(t)y = g(t)\]

라는 1계 선형미분 방정식의 초기 조건이 $y(t_0)=y_0$이고, $p(t)$와 $g(t)$가 열린구간 $I=(\alpha, \beta)$에서 연속이라고 하면, 이 구간에서 초기조건을 만족하는 함수 $y=\phi(t)$가 유일하게 존재한다.

왜냐면 $p(t)$와 $g(t)$가 구간 $I$에서 연속이라는 점을 생각하면 식 (11)과 같은 적분식을 정의할 수 있고, 초기 조건에 따른 적분 상수 $C$가 유일하게 결정될 수 있기 때문이다.