Geoffrey Hinton은 Andrew Ng과의 인터뷰에서 지금까지의 연구자로써의 인생에서 가장 자랑스러운 것을 꼽으라고 한다면 RBM을 이용한 연구성과를 꼽는다고 말한 바 있다.

RBM을 이용해서 Hinton이 기여한 것은 딥 뉴럴네트워크의 초기화가 얼마나 중요한 것인지 밝혀낸 것이다.

어떻게 초기화를 하는지가 딥 뉴럴네트워크가 효과적으로 학습되는지의 성패를 좌우할 수 있기 때문이다.

RBM은 generative model로 데이터들의 latent factor들을 확률적인 방법으로 얻어낼 수 있는 모델이다.

이번 post에서는 RBM이 어떤 방식으로 작동하는지 알아보고자 한다.

Prerequisites

RBM에 대해 잘 이해하기 위해선 다음의 내용에 대해 잘 알고 오는 것을 추천함.

• 최대우도법
• 경사하강법
• Rejection Sampling
• Monte Carlo Markov Chain

확률분포를 알 수만 있다면…

Restricted Boltzmann Machine(이하 RBM)은 Generative Model이라고 하는데, ANN, DNN, CNN, RNN 등과 같은 Deterministic Model들과 약간 다른 목표를 갖고 있다.

Deterministic Model들이 타겟과 가설 간의 차이를 줄여서 오차를 줄이는 것이 목표라고 한다면, Generative Model들의 목표는 확률밀도함수를 모델링하는 것이다.

확률 밀도 함수(probability density function, pdf)를 정확히 안다는 것은 무엇일까?

가령 얼굴을 그려주는 기계가 있다고 하자. 얼굴은 여러가지 요소로 구성되어 있는데, 가령 코를 그려준다고 해보자.

코 역시도 여러가지 다양한 가능한 경우의 형태로 구성되어 있다. 여기서 만약, 세상에 코의 형태가 동그라미, 세모, 네모 코만 있다고 가정했을 때,

우리가 이 세가지 형태의 코에 대한 확률밀도함수를 알 수 있다고 하자. 즉, 온 세상의 얼굴에서 코의 형태를 다 조사해 histogram을 그려보았다고 해보자.

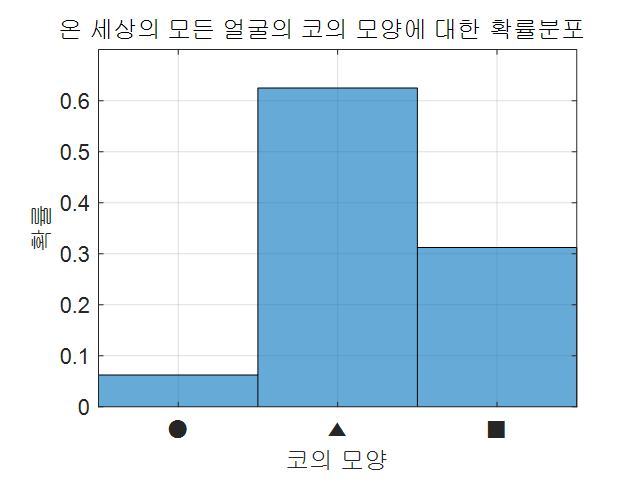
그림 1. 코의 모양에 대한 확률 분포

위의 그림을 보면 세모(▲) 모양의 코가 전 세상에서 가장 흔하다는 것을 알 수 있다.

아마 얼굴 그려주는 기계가 이런 확률 분포에 대해 알고 있다면 얼굴을 그릴 때 코에 대해서는 세모 모양의 코를 그려줄 가능성이 좀 더 높아 보인다.

이런 식으로 모든 가능한 경우에 대해 어떤 사건이 발생할 확률을 정확히 알 수 있다면, 여러 사건들의 조합으로 구성되는 사건(즉, 여기서는 전체 얼굴)을 일리있게 생성할 수 있게 되는 것이다.

실제로 Generative Model 중 요즘 유행하는 GAN(Generative Adversarial Networks)을 이용해 생성된 얼굴은 다음 그림에서 볼 수 있다.

그림 2. GAN을 이용해 만들어진 얼굴 변천사
그림 출처

이렇듯 확률밀도함수를 통해 결과물(여기서는 얼굴)을 생성해주는 과정을 샘플링(sampling)이라고 한다.

즉, Generative Model의 목적은 확률분포를 정확히 학습해 좋은 sample을 sampling하는 것이라고 정리할 수 있을 것이다.

확률밀도함수를 학습하기 위한 머신 설계

Boltzmann Machine

Boltzmann Machine은 이렇듯 확률분포(정확히는 확률질량함수 혹은 확률밀도함수)를 학습하기 위해 만들어졌다고 할 수 있다.

Boltzmann Machine이 가정하는 것은 “우리가 보고 있는 것들 외에도 보이지 않는 요소들까지 잘 포함시켜 학습할 수 있다면 확률분포를 좀 더 정확하게 알 수 있지 않을까?”라는 것이다.

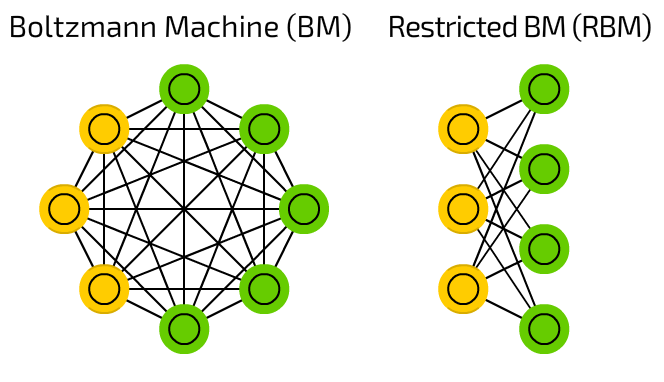
그림 3. Boltzmann Machine과 Restricted Boltzmann Machine
그림 출처

그림 3의 왼쪽에 보이는 것이 Boltzmann Machine이고 오른쪽에 보이는 것이 Restricted Boltzmann Machine이다.

우선 Boltzmann Machine에 대해서부터 설명하자면 동그랗게 생긴 것들이 가능한 이벤트들에 대한 state이다.

가령, 이 Boltzmann Machine이 얼굴의 형태에 관한 확률밀도함수를 학습하기 위해 만들어졌고, 각 동그라미들은 얼굴의 특정 부위에 대한 상태를 표시한다고 하자.

그 중 하나의 동그라미가 코에 관한 것이고, 상태 0, 1, 2가 동그라미, 세모, 네모 모양의 코에 대한 state를 각각 나타내는 것이라고 할 수 있겠다.

Boltzmann Machine에서 또 하나 주목할 점은 노란색과 초록색으로 표현된 특성인데, 각각은 hidden unit과 visible unit의 존재를 표현한 것이다.

hidden unit이 말하는 것은 우리가 보지 못하는 어떤 특성이 존재함을 암시하고, 이렇게 보이지 않는 factor들까지도 까지도 학습할 수 있다면 좀 더 정확한 확률분포를 학습할 수 있다는 것을 전제한다.

Restricted Boltzmann Machine

그렇다면 우리의 관심사인 Restricted Boltzmann Machine(RBM)은 뭘까?

RBM은 그림 3에서 오른쪽에 표시되어 있는데, RBM은 Boltzmann Machine에서부터 파생되어 나온 것으로 visible unit과 hidden unit에는 내부적인 연결이 없고, visible unit과 hidden unit 간의 연결만이 남아있는 형태이다.

이렇게 RBM을 구성한 것은 여러가지 확률 계산과 관련된 실용적인 이유가 있다.

우선은 visible, hidden layer의 node 간의 내부적인 연결이 없어진 것은 사건 간의 독립성을 가정함으로써 확률분포의 결합을 쉽게 표현하기 위해서이다.

또, visible layer와 hidden layer만을 연결해줌으로써 visible layer의 데이터가 주어졌을 때 hidden layer의 데이터를 계산할 수 있도록 하거나 혹은 hidden layer의 데이터가 주어졌을 때 visible layer의 데이터를 계산할 수 있도록 하는 ‘조건부 확률’을 계산할 수 있게 하는 것이다.

즉, $p(h,v)$는 계산하기 어려운 반면에 $p(h|v)$나 $p(v|h)$는 그나마 조금더 계산이 수월하기 때문이다.

이런 이유를 모아 한 마디로 쉽게 말하면 Boltzmann Machine의 계산이 너무 복잡해지니까 이를 편하게 하기 위해 덜 엄격한 모델을 구성한 것으로 볼 수 있다.

Boltzmann Machine에서 RBM과 같은 형태를 구성하게 됨으로써 생기는 독특한 점은 RBM은 Feed-Forward Nerual Network(FFNN) 처럼 학습하게 된다는 점이다.

뒤에 더 설명하겠지만, RBM의 작동방식은 FFNN과 유사하게 forward propagation을 통해 hidden unit의 상태를 결정하고, 다시 hidden unit의 상태로부터 back propagation을 함으로써 visible unit의 상태를 재결정하게 된다.

RBM의 구조와 특성

위에서 서술했듯이 RBM이 무언가를 학습한다는 것은 확률분포를 습득하는 것이다.

그렇다면 RBM이 학습을 잘 했다는 것을 어떻게 수학적으로 표현할 수 있을까?

그것을 알기 위해 우선은 RBM의 구조에 대해서 조금 더 자세하게 알아보도록 하자.

RBM의 구조

그림 4. RBM의 조금 더 구체적인 구조
그림 출처

RBM의 구조를 다시 한번 보면 visible layer와 hidden layer, 그리고 이 두 layer들을 연결해주는 weight matrix로 구성되어 있음을 알 수 있다.

거기에 더불어 visible layer와 hidden layer에는 bias term들이 포함되어 있다.

각각에 대해 설명하자면 다음과 같다.

• visible layer: 입력 데이터가 들어가는 곳. 각 입력 데이터들은 여러가지 상태(state)를 가질 수 있음. 앞으로 표기는 $v$.
• hidden layer: 은닉 데이터가 샘플링되어 나오는 곳. 각 은닉 데이터들은 여러가지 상태를 가질 수 있음. 앞으로 표기는 $h$.
• weight matrix: visible layer와 hidden layer를 연결해주는 장치. 원래의 Boltzmann Machine에서부터 파생되어 나온 개념. 앞으로 표기는 $W$.
• bias for visible layer: 입력 데이터의 내재적 특성(inherent property)을 설정해주는 부분. 후술하겠지만, 어떤 visible unit이 거의 항상 1인 경우라면 해당 unit의 bias는 높을 수록 좋음. 앞으로 표기는 $b$.
• bias for hidden layer: 은닉 데이터의 내재적 특성을 설정해주는 부분. 위의 visible layer의 bias와 유사한 역할. 앞으로 표기는 $c$.

참고로 위의 $v, h, b, c$는 모두 벡터이며 $W$는 행렬이다.

visible layer의 node 개수가 $d$개, hidden layer의 node 개수가 $n$개라고 했을 때, 각각의 차원은 다음과 같다.

이와 같은 구조를 갖는 RBM에 대해 ‘학습을 잘 하고 있음’을 표현해주는 것은 어떻게 가능할지 계속해서 알아보도록 하자.

Energy: Configuration을 반영하는 수치

RBM이 학습을 잘 했다는 것을 수치적으로 판단하기 위해서는 여타 model들을 구성할 때와 마찬가지로 cost function을 정의해주어야 한다.

RBM의 cost function은 독특하게 “Energy”라는 개념을 이용해 정의되게 될텐데, 이 energy라는 개념은 물리학에서 차용한 것이라고 한다.

특정 상태 $x$에 대한 에너지를 $E(x)$라고 한다면, 이 에너지 $E(x)$는 그 상태(configuration)에 매칭되는 값임을 말한다.

즉, 상태 $x$에 대한 사건들의 분포를 말해주기도 하므로, 이는 확률분포와 연결시켜 생각할 수 있다.

다항분포로부터 가능한 모든 경우의 $x$에 대한 energy 함수 중, 우리가 원하는 $x$에 대한 에너지를 얻을 확률을 계산하면 다음과 같이 특정 상태 $x$에 대한 확률값을 계산할 수 있게 된다.

그런데, 우리는 RBM에서 visible units $v$와 hidden units $h$의 상태에 따라 에너지를 결정할 수 있게 되는데, 결국 우리가 관찰할 수 있는 것은 visible units $v$에 의한 energy 이므로 다음과 같이 visible units의 확률 분포를 결정할 수 있다.

여기서 hidden units에 대한 개념을 도입하다보니 식 (4)가 식 (6)처럼 복잡해졌기 때문에 다음과 같이 치환해 식(6)을 식(4)처럼 만들어주도록 하자.

여기서 $F(\cdot)$을 Free Energy라고 이름 붙이도록 하자.

한편, RBM에서 Energy는 다음과 같이 정의한다.

여기서 $’$ 표시는 전치(transpose)이다. 다시 말해 $b’v$는 $b$ 벡터와 $v$ 벡터의 내적을 의미한다.

RBM은 에너지를 식 (11)과 같이 정의했을까? 그것은 $b, c, W$에 관한 설명을 통해 확인할 수 있는데, 특히 $b$와 $c$는 visible layer와 hidden layer의 bias term으로 visible layer의 내재적 특성과 hidden layer의 내재적 특성을 설정한다고 설명한 바 있다.

즉, 주어지는 데이터의 특성에 맞게 이 bias term들이 변형되어야 한다. 이 bias term들은 특정 visible unit 혹은 hidden unit이 얼마나 자주 “ON” 상태가 되어있는지에 따라 값이 커지도록 설정될 것이다. 어떤 visible unit이 거의 항상 1인 경우라면 해당 unit의 bias는 높을 것이고 이에 따라, 식 (11)에서 에너지 값이 떨어질 것이다. 낮은 에너지는 안정적인 상태를 의미한다.

두 가지의 상태만 갖는 RBM

많은 RBM의 연구에서 visible unit 혹은 hidden unit은 0 또는 1의 상태만 갖는 RBM을 다룬다.

(이렇듯 0 또는 1의 상태만 갖는 RBM을 Bernoulli RBM이라고도 한다.)

추후에 더 자세하게 알게 되겠지만, 우리는 energy의 개념을 이용해 RBM이 학습이 잘 되고 있는지를 알 수 있다. 식 (11)의 Energy의 식을 이용해 RBM의 학습 과정을 전개해나가면 식이 워낙에 복잡해지기 때문에 식 (9)의 Free energy의 수식을 이용해 학습 과정이 전개될 것이다.

따라서, 우리는 우선 Free Energy의 수식을 조금 더 전개해보도록 하자.

$exp(b’v)$에는 $h$와 관련된 term이 없으므로 summation 밖으로 빼오면,

$\log(\exp(x))$는 $x$와 같다. 따라서,

여기서 $h\in{0, 1}$ 이므로,

여기서 $W_i$는 $W$의 $i$번째 행으로 부터 얻은 행벡터를 의미한다.

또, RBM은 그 독특한 형태로 인해 visible layer의 데이터를 이용해 hidden layer의 데이터를 샘플링할 수 있고, 또 반대로 hidden layer의 데이터를 이용해 visible layer를 다시 샘플링할 수도 있다.

따라서, 우리는 visible layer의 데이터가 주어졌을 때 hidden layer의 데이터를 샘플링할 때의 조건부 확률을 계산할 수 있다. (혹은 반대로 hidden layer의 데이터가 주어졌을 때 visible layer의 데이터를 샘플링할 조건부 확률을 계산할 수도 있을 것이다.)

여기서 총 $n$개의 hidden layer unit 중 $i$번 째 hidden layer의 unit이 1로 샘플링될 확률 $p(h_i=1|v)$를 계산하자.

Bernoulli RBM에서는 $h\in\lbrace 0, 1\rbrace$ 이므로,

여기서 $\sigma(\cdot)$은 sigmoid 함수이다.

마찬가지 방법으로

이다.

$W_j’$은 $W$ 행렬의 $j$번재 열로부터 얻은 행벡터를 의미한다.

RBM의 학습 과정

RBM 학습 과정의 큰 그림

이제는 RBM 학습에 필요한 어지간한 기초 수식들이 전개가 되었다.

그렇다면 RBM을 학습시킨다는 것은 무엇일까?

RBM은 확률 분포를 학습하는 것이 목표라고 할 수 있는데, RBM이 확률 분포를 학습하는 과정은 sampling을 통해서 간접적으로 확인할 수 있다.

RBM이 어떤 주어진 데이터를 잘 학습했다면 sampling을 통해 얻은 visible layer의 데이터가 원래 데이터와 거의 같아야 한다.

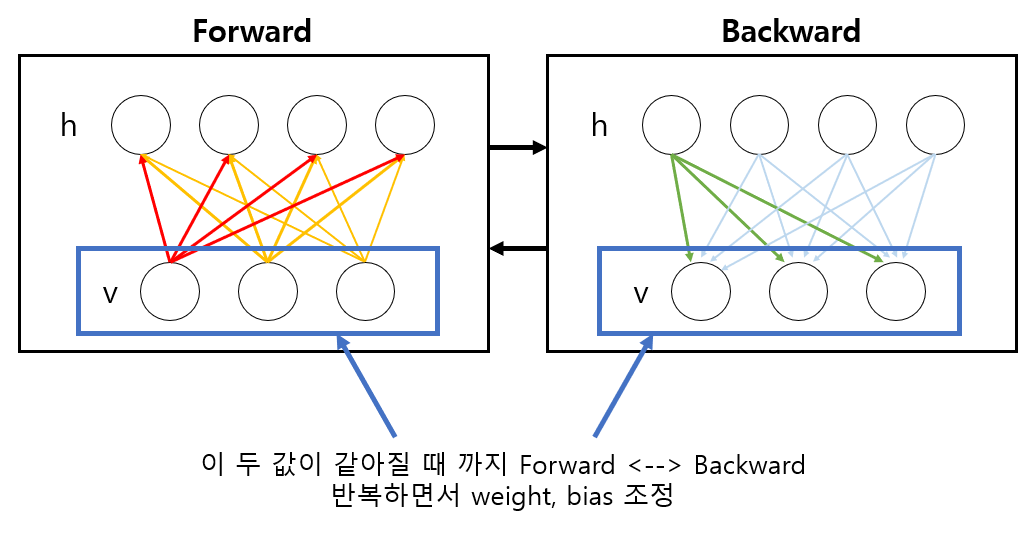
그림 4. RBM을 학습시킨 다는 것의 의미: sampled visible layer의 값이 원래의 visible layer의 값과 같아진다.

이러한 과정을 수식적으로 유도해도보록 하자.

Gradient Descent를 이용한 RBM의 학습

sampling을 통해 얻은 visible layer의 데이터가 원래의 데이터와 거의 같은 형태를 가지고 있을 때 RBM이 잘 학습되었다는 것은 임의로 설정한 학습 목표가 아니다.

관련 내용을 수학적으로 확인해보고자 한다.

RBM의 파라미터들($b, c, W$)이 잘 학습되었다면 현재 데이터들을 가지고 얻은 모든 likelihood의 곱이 최대가 될 것이다.

(이 문장이 이해가 안된다면 꼭 최대우도법 편을 공부하고 오는 것을 추천한다!)

다시 말해, 우리는 식 (8)에서 visible layer를 통해서 확인할 수 있는 확률에 대해 정의한 바 있는데 우리가 RBM의 파라미터들을 잘 학습하기 위해서는 결국 식 (8)의 확률함수를 이용해 지금 얻은 데이터들을 통해 얻은 확률밀도함수의 높이를 모두 곱했을 때 최대가 되어야 한다는 것이다.

하지만, 학습과정이라는 것은 애초에는 학습이 덜 되어 있다는 뜻이므로 likelihood(즉, 모든 데이터들을 통해 얻은 확률밀도함수의 높이를 곱한 것)를 최대화 시켜주기 위해 Gradient ascent 방법을 이용할 수 있다. 그런데 보통은 어떤 모델을 학습할 때에는 경사하강을 시켜주기 때문에 likelihood에 -1을 곱해준 negative likelihood를 최소화 시켜주도록 하자. 그래서 우리는 Gradient Descent 방법을 이용하도록 하자.

또, 보통은 likelihood를 직접이용하기 보다는 log-likelihood를 이용하는 것이 일반적이므로 negative log-likelihood를 최소화 시켜줄 수 있도록 식을 계산해보도록 하자.

RBM의 파라미터들을 $\theta$라고 통칭하도록 하자. 이제, 식 (8)로부터,negative log-likelihood는 아래와 같이 계산될 수 있다.

여기서 $\tilde v$는 RBM 모델에 의해 생성된 visible unit들에 들어가는 샘플이다.

기댓값의 정의에 의거하여,

기댓값 연산은 실제로는 구할 수가 없기 때문에 sampling을 통해서 얻어지는 visible layer들의 데이터들을 $\mathcal{N}$이라고 했을 때 아래와 같이 생각할 수 있다.

가장 마지막의 식을 보면 결국은 처음 입력으로 넣어준 visible layer의 데이터 $v$에 대한 Free energy와 sampling을 통해 얻은 visible layer의 데이터 $\tilde{v}$의 free energy의 차이가 loss로 이용되었음을 알 수 있다.

즉, RBM에서 loss가 낮다는 것은 sampling을 통해 얻은 visible layer의 데이터가 원래의 데이터와 거의 같은 형태를 가지고 있다는 것을 다시 한번 확인할 수 있게 된다.

결국 RBM에게 학습이란: Contrastive Divergence를 줄이는 것

Contrastive Divergence(CD)란 visible layer에 데이터를 주고 hidden layer의 node 값을 샘플링, 그런 다음 다시 visible layer의 데이터를 다시 예측하도록 하는 과정에서 처음 주어진 visible layer의 데이터와 다시 획득한 visible layer의 데이터가 얼마나 차이가 있는지를 말하는 것이다.

만약 weight matrix와 hidden layer의 bias가 잘 학습되었다면 hidden unit을 잘 sample 해줄 수 있을 것이고 그렇다면 재획득한 visible layer의 데이터는 원래의 데이터와 일치할 것이기 때문이다.

여기서 Hinton 교수는 visible layer의 데이터를 단 한번만 샘플링해서 loss를 계산하더라도 RBM의 학습에는 큰 어려움이 없다는 것을 실험적으로 확인하였다.

즉, 원래의 데이터로부터 얻은 visible layer의 free energy와 생성된 데이터로부터 얻은 visible layer의 free energy 간의 차이가 적을 수록 학습이 잘 된 것이라고 할 수 있으므로 loss는 다음과 같이 생각할 수 있다.

Sampling 과정

그렇다면 visible layer 혹은 hidden layer의 데이터들은 어떻게 샘플링할 수 있는 것일까?

Gibbs sampling은 Markov Chain Monte Carlo의 한 방법으로 구분된다.

Markov Chain의 특성을 이용해 sampling하는 것이기 때문에 RBM의 sampling을 Gibbs Sampling으로 볼 수 있다고 생각한 것으로 보인다. 이름은 어렵고 현란해 보이지만 결국은 likelihood 비교를 통한 Accept/Reject에 불과한 것이다.

RBM에서 $\vec{v}$와 $\vec{h}$가 Markov property를 가진다는 것은 $l$번 째 state의 $\vec{v}^{(l)}$과 $P(\vec{h}^{(l)}|\vec{v}^{(l)})$을 통해 $\vec{h}^{(l)}$을 유추해낼 수 있다는 것을 의미한다. (여기서 $\vec{v}$와 $\vec{h}$의 순서는 바뀔 수 있다.) 즉 다음과 같은 과정을 통해 $\vec{v}$와 $\vec{h}$를 얻을 수 있다.

Step 1. Sample $\vec{h}^{(l)}$ ~ $P(\vec{h}|\vec{v}^{(l)})$

$\quad\Rightarrow$ We can simultaneously and independently sample from all the elements of $\vec{h}^{(l)}$ given $\vec{v}^{(l)}$.

Step 2. Sample $\vec{v}^{(l+1)}$ ~ $P(\vec{v}|\vec{h}^{(l)})$

$\quad \Rightarrow$ We can simultaneously and independently sample from all the elements of $\vec{v}^{(l+1)}$ given $\vec{h}^{(l)}$.

여기서 superscript $^{(l)}$또는 $^{(l+1)}$ 등은 $(l)$번째 또는 $(l+1)$번째 상태의 $\vec{v}$ 혹은 $\vec{h}$를 의미한다.

조금 더 구체적으로 설명하자면, $\vec{c},\vec{b}, W$를 모두 안다고 가정해보자. 즉, training이 모두 끝났다고 가정하도록 하자. 여기서 $\vec{v}$는 우리가 알 수 있는 것이다. 그러면 $P(h_j = 1 | \vec{v})$는

로부터 그 값을 도출할 수 있게 된다. 가령 $P(h_i =1 | \vec{v}) = 0.2$라는 값을 얻었다고 해보자. 이때, uniform distribution에서 random하게 0~1 사이의 숫자를 얻자. 그러면 다음과 같은 방식으로 $h_j$가 0인지 1인지를 결정할 수 있다.

num = rand(1);

if num < $P(h_j = 1| \vec{v})$

$\quad\Rightarrow h_j = 1$

else

$\quad\Rightarrow h_j = 0$

end

RBM 의 학습 코드 (Python)

RBM의 학습 코드는 Python을 기반으로 했으며 Pytorch를 이용해 최적화하였다.

Pytorch로 포팅한 코드의 출처는 이곳이며, 원래의 Theano를 이용해 포팅했던 소스코드는 이곳이 참고 되었음을 밝힌다.

#!/usr/bin/env python
# coding: utf-8
"""
RBM 원래 코드 출처: https://github.com/odie2630463/Restricted-Boltzmann-Machines-in-pytorch
공돌이의 수학정리노트 - RBM편
"""
import numpy as np
import torch
import torch.utils.data
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
from torchvision import datasets, transforms
from torchvision.utils import make_grid
 
 
#%% 시각화를 위해 필요한 함수
 
# get_ipython().run_line_magic('matplotlib', 'inline') # inline 출력 필요한 경우 주석 처리 제거할 것.
import matplotlib.pyplot as plt
 
def show_adn_save(file_name,img):
    """
    이미지 출력해주고 세이브 해주는 역할의 함수
    """
    npimg = np.transpose(img.numpy(),(1,2,0))
    f = "./%s.png" % file_name
    plt.imshow(npimg)
    plt.imsave(f,npimg)
 
 
#%% RBM 모듈 만들기
class RBM(nn.Module):
    def __init__(self,
                 n_vis=784,
                 n_hin=500,
                 k=5):
        super(RBM, self).__init__()
        # 여타 initialization에 비해 이와 같은 방식이 학습이 제일 잘 됨.
        self.W = nn.Parameter(torch.randn(n_hin,n_vis)*1e-2) 
        self.v_bias = nn.Parameter(torch.zeros(n_vis)) # bias는 0으로 초기화.
        self.h_bias = nn.Parameter(torch.zeros(n_hin)) # bias는 0으로 초기화.
        
        self.k = k # Contrastive Divergence의 횟수
    
    def sample_from_p(self,p):
        # Gibbs Sampling 과정
        # 확률 계산 후 uniform distribution으로부터 얻은 값 보다 크면 1, 아니면 -1로 출력하고
        # relu 함수를 이용해 -1로 출력된 값들은 모두 0으로 처리해버림.
        p_ = p - Variable(torch.rand(p.size()))
        p_sign = torch.sign(p_)
        return F.relu(p_sign)
    
    def v_to_h(self,v):
        # 주어진 visible units로부터 hidden unit을 sampling하는 과정
        p_h = torch.sigmoid(F.linear(v,self.W,self.h_bias))
        sample_h = self.sample_from_p(p_h)
        return p_h,sample_h
    
    def h_to_v(self,h):
        # hidden unit의 샘플로부터 visible unit을 다시 복원해보는 과정
        p_v = torch.sigmoid(F.linear(h,self.W.t(),self.v_bias))
        sample_v = self.sample_from_p(p_v)
        return p_v,sample_v
        
    def forward(self,v):
        # RBM에서 forward propagation은 visible -> hidden -> 다시 visible로 
        # hidden unit과 visible unit을 샘플링 하는 과정을 말함.
        pre_h1,h1 = self.v_to_h(v)
        
        h_ = h1
        for _ in range(self.k): # Contrastive Divergence를 k 번 수행함.
            pre_v_,v_ = self.h_to_v(h_)
            pre_h_,h_ = self.v_to_h(v_)
        
        # 아래의 v는 입력으로 들어온 v이고 v_는 sampling으로 얻은 h로부터 다시 획득한 입력 샘플
        return v,v_
    
    def free_energy(self,v):
        # Free Energy 계산
        vbias_term = v.mv(self.v_bias) # mv: matrix - vector product
        wx_b = F.linear(v,self.W,self.h_bias)
        
        temp = torch.log(
            torch.exp(wx_b) + 1
            )
        hidden_term = torch.sum(temp, dim = 1)
        
        return (-hidden_term - vbias_term).mean()
 
 
#%% 데이터 셋 불러오기: MNIST 이용
batch_size = 64
train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./MNIST_data', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor()
                   ])),
    batch_size=batch_size)
 
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./MNIST_data', train=False, transform=transforms.Compose([
                       transforms.ToTensor()
                   ])),
    batch_size=batch_size)
 
 
#%% RBM 모델 객체 및 최적화 함수 객체 만들기
 
rbm = RBM(k=1) # CD의 k = 1로 설정. 
# 즉, visible unit을 딱 한번만 sampling 해주고 
# 그걸로 원래의 visible unit의 데이터와 configuration 비교해서 loss로 삼겠다는 의미.
train_op = optim.Adam(rbm.parameters(), 0.005) # 어떤 Optimizer를 넣어줘도 무관함.
 
#%% RBM 학습
 
for epoch in range(10):
    loss_ = []
    for _, (data,target) in enumerate(train_loader): # Stochastic Gradient Descent 수행함.
        data = Variable(data.view(-1,784))
        sample_data = data.bernoulli() # RBM의 입력은 0 또는 1의 값만 가져야 함.
        
        v,v1 = rbm(sample_data)
        loss = rbm.free_energy(v) - rbm.free_energy(v1)
        loss_.append(loss.data.item())
        train_op.zero_grad()
        loss.backward() # RBM의 Backpropagation은 원래의 입력과 sampling 된 입력간의 차이를 줄여주는 과정
        train_op.step()
    
    print(np.mean(loss_))
 
#%% Test Data로부터 원본 데이터와 샘플링된 입력 데이터를 비교해보자.
 
testset = datasets.MNIST('./MNIST_data', train=False, transform=transforms.Compose([
                       transforms.ToTensor()
                   ]))
 
sample_data = testset.data[:32,:].view(-1, 784) # 총 32개 데이터를 받아옴.
sample_data = sample_data.type(torch.FloatTensor)/255.
 
v, v1 = rbm(sample_data)
show_adn_save("real_testdata",make_grid(v.view(32,1,28,28).data))
show_adn_save("generated_testdata",make_grid(v1.view(32,1,28,28).data))

RBM 학습 결과

그림 5. RBM을 학습시킨 결과. 원래의 visible layer에 들어가는 데이터들과 sampling을 통해 얻어낸 visible layer의 데이터.

참고 자료

• Introduction to Restricted Boltzmann Machine, Edwin Chen
• Restricted Boltzmann Machine, DeepLearning 0.1 Documentation
• What is the difference between autoencoders and a restricted Boltzmann machine?
• Ali Ghodsi, Lec [7], Deep Learning , Restricted Boltzmann Machines (RBMs)