※ 윌콕슨 순위합 검정(Wilcoxon rank sum test)은 맨-휘트니 U 검정(Mann-Whitney U test)와 동등한 테스트입니다.
※ 이 포스팅의 내용은 Stanton Glantz의 Primer of biostatistics 교재를 참고하여 작성되었습니다.
Prerequisites
이 포스팅을 더 잘 이해하기 위해선 아래의 내용에 알고 오시는 것이 좋습니다.
Motivation
지금까지 배웠던 모수기반의 통계 기법인 t-test와 ANOVA는 다음과 같은 가정에 기반하여 고안된 테스트이다.
“샘플 데이터들이 정규 분포 형태의 분포를 가진 모집단에서 부터 추출되었으며, 처치에 의해 평균 값이 변하더라도 분산값은 달라지지 않는다.”
많은 경우에서 샘플 데이터들이 정규 분포로부터 추출되었다고 볼 수 있고, 샘플 수가 많으면 샘플 평균은 정규 분포를 따르기 때문에($\because$ 중심극한정리) 위와 같은 가정은 타당한 경우가 많다. 이 때문에 t-test나 ANOVA는 아주 널리 쓰이는 통계 기법이라고 할 수 있다.
그런데, 이런 가정을 만족하지 못하는 데이터의 경우에는 모수 검정법을 사용할 수는 없고 비모수 검정법을 사용해야 한다. 다시 말해 모집단의 분포가 정규 분포라고 확신하기 어려운 경우나 데이터 샘플 수가 너무 적은 경우에는 비모수 검정을 사용하는 것을 고려해볼 수 있다. 뿐만 아니라 데이터를 측정했을 때 연속적인 수치값이 나오지 않고 등수만 나오는 경우에도 마찬가지로 모수검정법을 사용할 수는 없으므로 비모수 검정법을 사용하는 것을 고려해볼 수 있다.
이번 챕터에서는 independent t-test를 대체할 수 있다고 알려진 윌콕슨 순위합 검정(Wilcoxon rank sum test)에 대해 알아볼 것이다. 다시 말해 독립적으로 추출된 두 표본 집단을 비교함에 있어 정규성 가정을 두지 않고 통계적인 비교를 할 수 있는 기법에 대해서 알아보고자 한다.
순위합 검정
순위합 검정의 원리 소개
순위합 검정이라고 해서 특별히 t-test와 원리가 크게 다른 것은 아니다. t-value의 의미와 스튜던트의 t 테스트 편에서 어떻게 t값의 분포를 생각했는지 다시 한번 떠올려보자.
먼저, 우리는 통계량 t-값을 정의했다. 그 뒤, 시뮬레이션을 통해 모집단에서 추출될 수 있는 두 표본 집단을 랜덤하게 선택하고 그때마다 나오는 t-값의 분포를 확인했다.
아래 그림은 모집단의 수가 150이고 n=6인 표본을 두 개 뽑는 과정을 100번 반복하면서 t-값의 분포를 시뮬레이션 한 것이다.
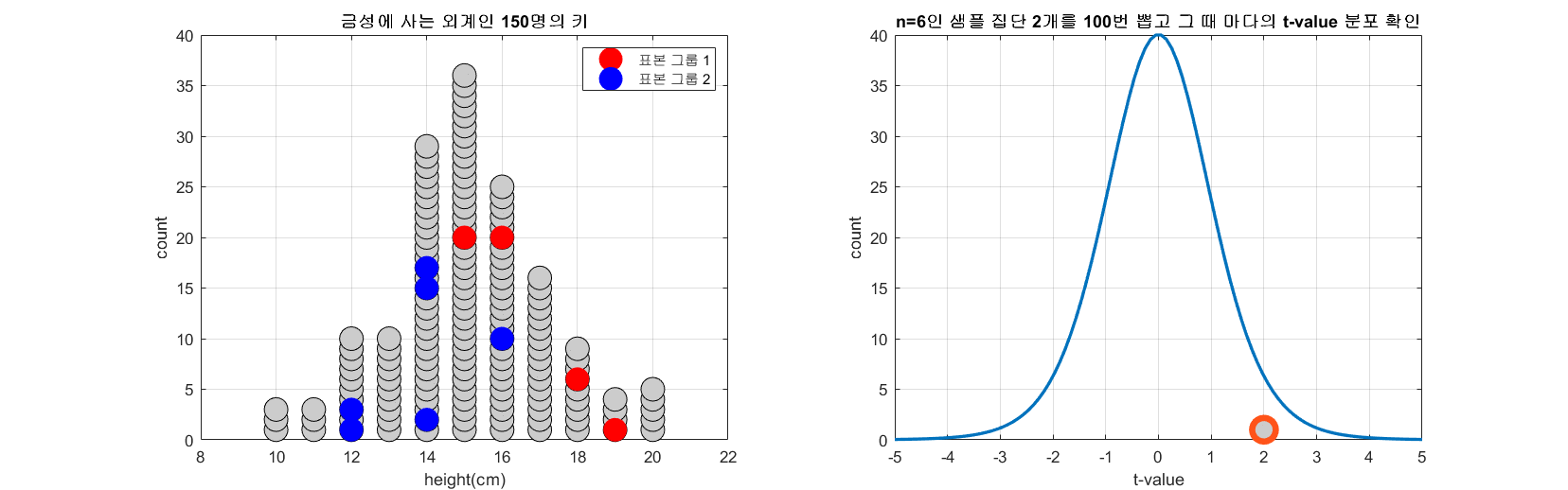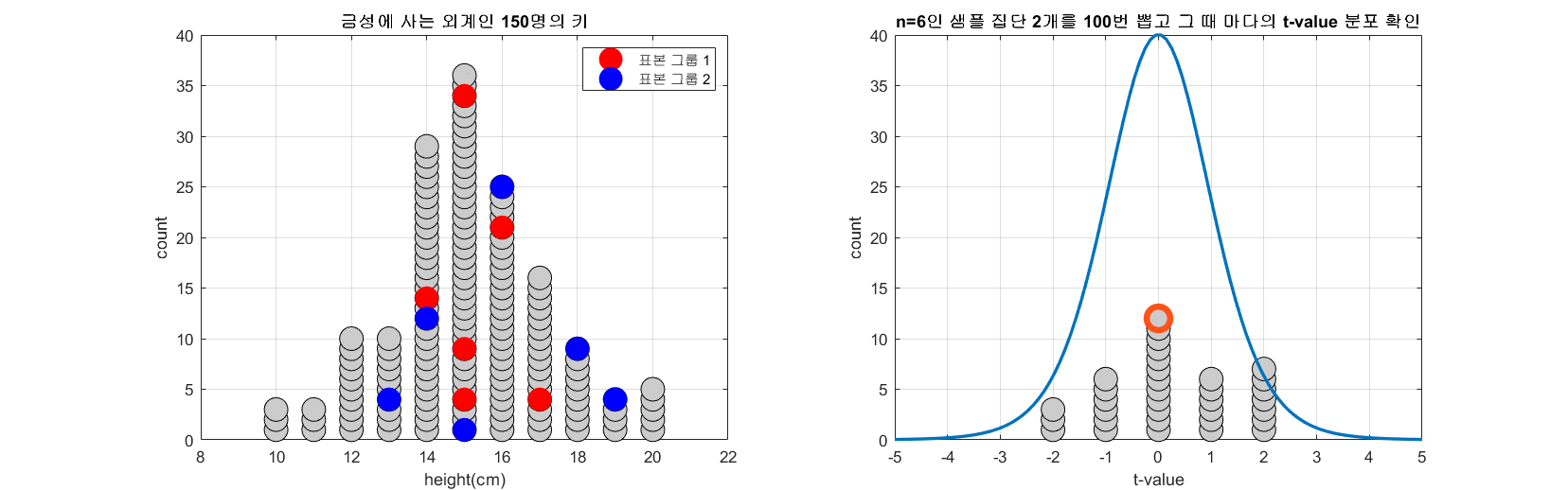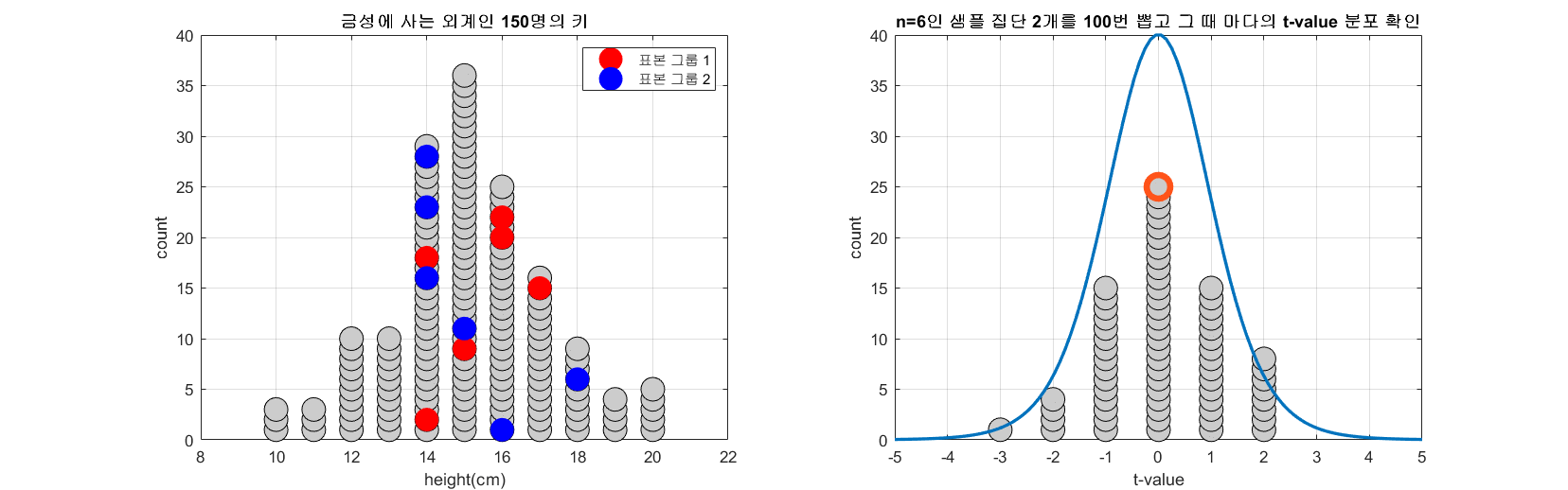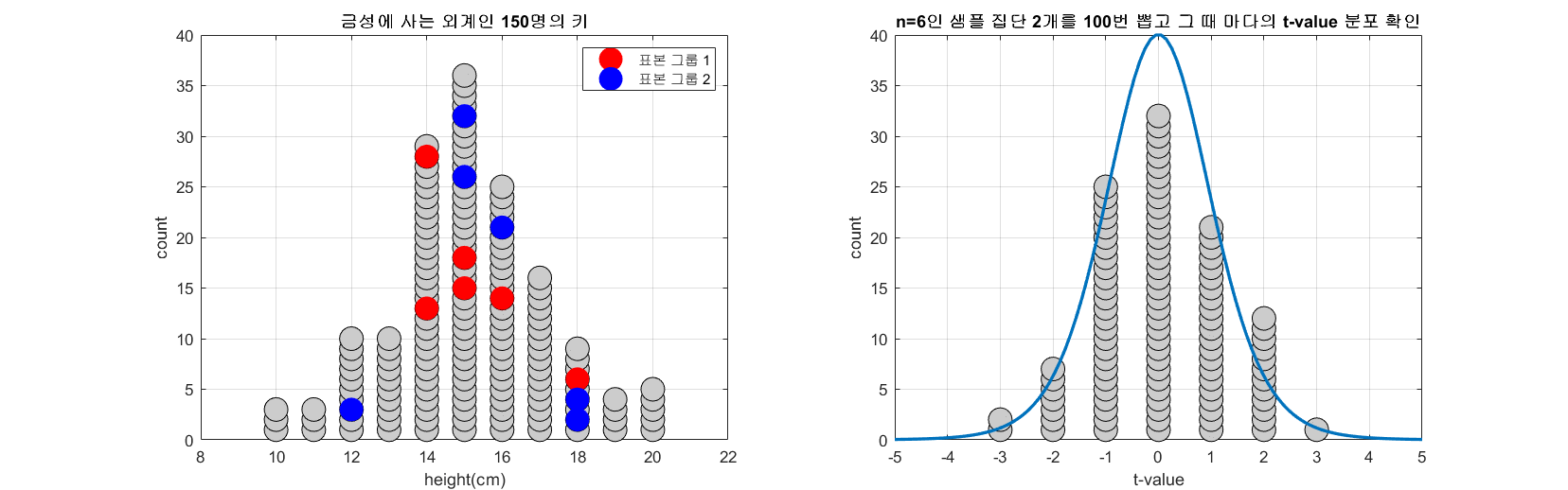
그림 1. 100 번 n=6인 두 개의 표본 그룹을 추출해보고 그 때 마다 얻게되는 t-value를 그린 것
순위합 검정도 이 과정과 크게 다르지 않다. 우리는 위의 t-값과 같은 역할을 할 통계량을 먼저 정의한 뒤, 시뮬레이션을 통해 획득할 수 있는 모든 가능한 통계량의 분포를 확인할 것이다.
그런 다음 우리에게 주어진 데이터의 통계량 값이 얼마나 큰지를 점검함으로써 지금 갖고 있는 두 표본집단이 정말 유의하게 다르다고 할 수 있는지 보고자 한다.
아래 그림은 우리에게 주어진 예시 데이터이다. 이 데이터는 이뇨제의 효과를 보기 위한 가상의 실험 데이터이다. (출처: S. Glantz의 책 Primer of Biostatistics)
두 그룹으로 데이터가 나눠져있는데, 한 그룹은 플라시보 약을 복용한 그룹이고 다른 한 그룹은 이뇨제를 복용한 그룹이다.
플라시보 그룹은 총 세 명, 이뇨제 복용 그룹은 총 4명이며, 각 피험자들의 소변량이 표시되어 있다.
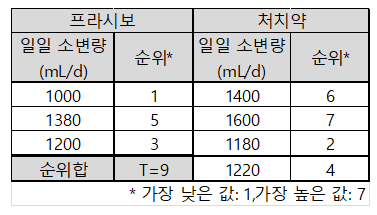
그림 2. 순위합 검정을 설명하기 위한 예시 데이터. 이뇨제 복용에 관한 실험 데이터
출처: Primer of Biostatistics, 7th ed., S. Glantz
이 데이터를 보면 우선 그룹 내의 샘플 수가 아주 한정적인 것을 알 수 있다. 따라서, 표본 수가 적기 때문에 비모수 검정을 수행할 수 있는 사례라고도 볼 수 있을 것이다.
비모수 검정, 특히 순위를 이용한 검정을 수행하기 위해서는 가장 먼저 각 데이터들의 값을 이용해 데이터들의 순위를 계산하는 것이다.
여기서는 가장 값이 작은 데이터를 순위 1, 가장 값이 큰 데이터를 순위 7로 두고 계산하였다.
(혹시나 데이터 순위를 거꾸로 가장 값이 작은 데이터를 순위 7로 하고, 가장 값이 큰 데이터를 순위 1로 하더라도 분석 결과에는 영향이 없다.)
그럼, 그림 2에서 볼 수 있는 것 처럼 우리는 ‘순위합’이라는 통계량을 계산해주자.
그림 2 왼쪽의 플라시보 그룹은 총 순위합 $T$ 값이 9라는 것을 알 수 있다.
그럼 여기서 우리가 직면하는 문제는 다음과 같다.
"과연 이 T = 9라는 값은 충분히 작다고 말할 수 있는 값일까?"
이제, t-value의 의미와 스튜던트의 t 테스트에서 t-분포를 생각했던 것 처럼 우리는 순위합 통계량 $T$의 분포를 확인해볼 수 있다.
총 7개의 순위(1~7) 중 세 개를 골라내는 경우의 수만 생각해준다면 순위합 통계량 $T$가 가질 수 있는 모든 경우의 수에 관한 분포를 알 수 있게 되는 것이다.
따라서, 아래의 그림 3과 같이 7개의 순위 중 세 개를 선택하는 경우의 수에 대해 모두 생각해보고, 각 경우의 수에 대응되는 순위합 통계량 $T$를 계산해보자.
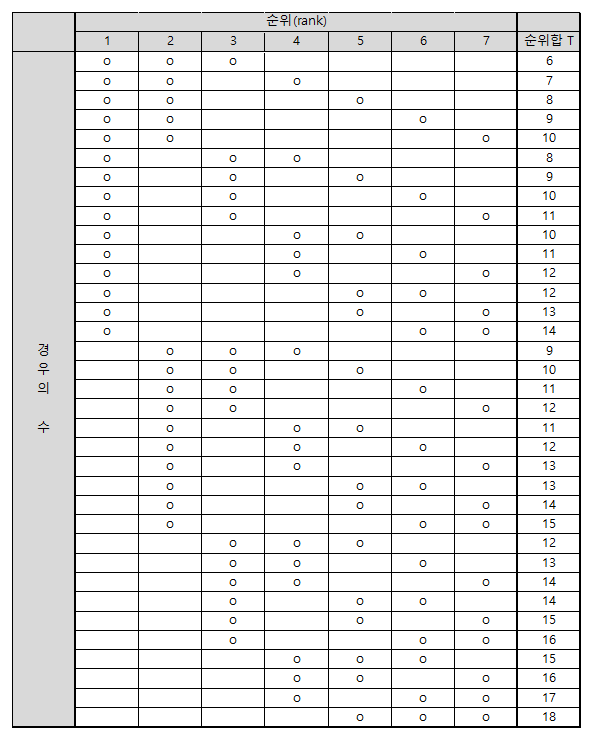
그림 3. 7개 중 3개의 순위를 선택하는 경우의 수와 각 경우의 수에 해당하는 순위합 통계량 $T$
가령, 첫 번째 행에서는 1, 2, 3위의 데이터가 플라시보 그룹일 경우를 상정한 것이며, 이 때의 순위합 통계량 $T$는 6이 된다.
그림 3에서와 같이 가능한 경우의 수에 대한 통계량 $T$가 모두 조사되었다면 가능한 통계량 $T$에 대한 histogram을 그려보자.
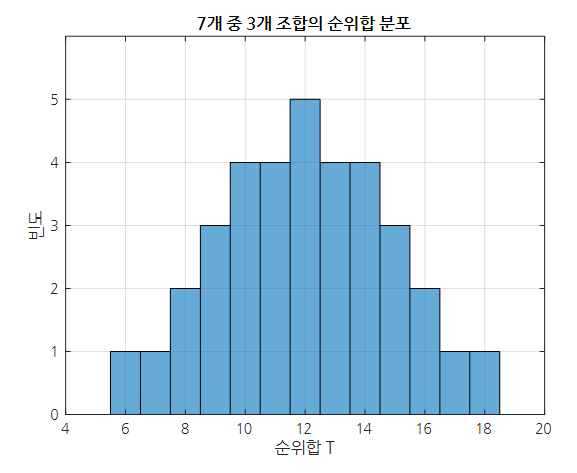
그림 4. 모든 가능한 조합에 해당되는 순위합 통계량 $T$의 히스토그램
이렇게 해놓고 보면 가장 극단적인 케이스는 $T=6$ 이거나 $T=18$인 경우인 것을 알 수 있으며, 이마저도 총 35개의 케이스 중 1번째 혹은 마지막 케이스이기 때문에
실제로는 치료 약물의 효과가 없는데도 우연히 $T=6$ 혹은 $T=18$인 경우에 해당하는 $T$ 값을 얻을 확률(즉, p-value)은
\[2\times \frac{1}{35} = 0.057\]임을 알 수 있다. (양측 검정이라고 생각하여 2를 곱했다.)
그러므로 우리가 갖고 있는 데이터의 $T=9$는 사실상 두 그룹 간 차이를 보여주기 어려운 케이스가 된다고 결론지을 수 있다.
눈여겨 볼 점은 얻을 수 있는 가능한 $T$값은 모두 순위들의 조합으로 얻어지는 것이므로 이산적(discrete)할 수 밖에 없고, p-value 또한 연속적인 값으로 나오지 않을 수 있다는 점이다.
아래의 표에서는 실험 조건에 따른 유의한 순위합 통계량 $T$를 정리해 둔 것이다. $n_S$는 두 그룹 중 샘플이 적은 쪽의 샘플 수, $n_B$는 샘플이 많은 쪽의 샘플 수를 의미한다.
그리고, 모수 기법에서 주요하게 사용하는 p-value 인 $p=0.05$와 $p=0.01$과 가장 가까운 $p$값을 기재해 두었다.
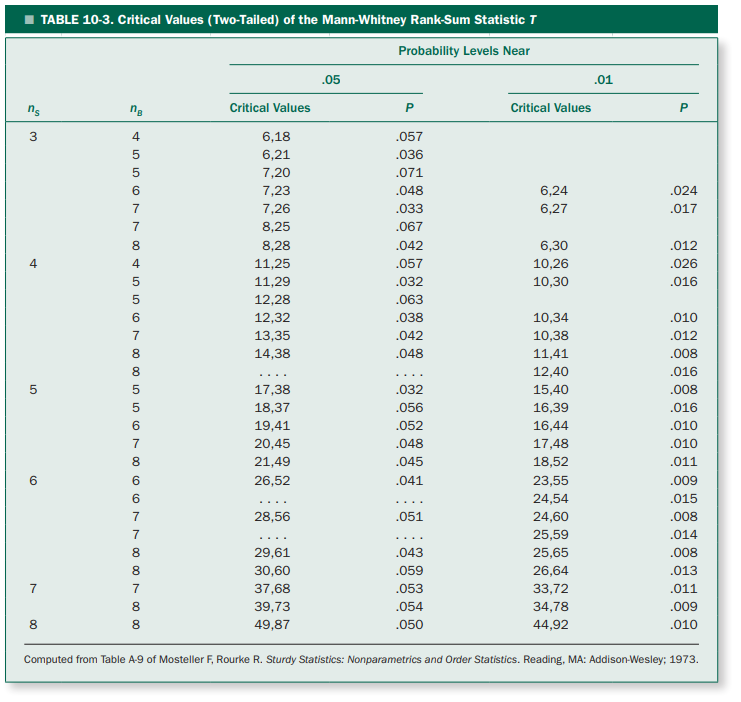
그림 5. 실험 조건에 따른 유의한 순위합 통계량 $T$와 그에 해당하는 p-value
출처: Primer of Biostatistics, 7th ed., S. Glantz
순위합 검정의 정규 근사
분석을 하다보면 샘플 수가 많음에도 비모수 검정을 사용해야 할 때도 있을 것이다.
가령, 두 집단의 샘플수가 10명씩 있었다고 해보자. 이런 경우 20개 순위 중 10개를 선택하는 방법의 가지수는
\[_{20}C_{10}=184,756\]개나 되기 때문에 모든 것을 표로 다 적어서 정리하기는 어렵다. 따라서, 이런 경우에는 정규 근사를 이용한다. 알려진 바로는 수가 많은 쪽의 그룹에 8개 이상의 샘플이 들어있는 경우에는 아래와 같은 평균, 표준편차를 가지는 정규분포에 근사한다고 알려져 있다.
\[\mu_T=\frac{n_S(n_S + n_B + 1)}{2}\] \[\sigma_T=\sqrt{ \frac{n_Sn_B(n_S+n_B+1)}{12} }\]따라서 우리는 $T$를 다음과 같은 통계량 $z_T$로 바꿔 쓰게 되면 정규 분포에 대한 검사가 가능한 것이다.
\[z_T = \frac{T-\mu_T}{\sigma_T}\]여기서 continuous correction이라는 수정을 한번 더 거칠 수 있는데, 이 과정은 $T$의 분포가 이산적이었다보니 $z$와 같은 연속분포에 맞춰줄 때 생기는 이산 오류를 바로잡는 것에 목적이 있다.
\[\Rightarrow z_T = \frac{ \left| T-\mu_T \right|-1/2 }{ \sigma_T }\]참고문헌
- Primer of biostatistics, 7th ed., S. Glantz / Ch. 10 Alternatives to Analysis of Variance and the t Test Based on Ranks