이 포스팅은 Nathan Kutz 교수님의 강의를 많이 참고 하여 작성한 것임을 미리 밝힙니다.

Prerequisites

이 포스팅을 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 고윳값과 고유벡터
• 선형 연산자와 함수 공간

에르미트 행렬 소개

에르미트(Hermitian) 행렬은 자기 자신과 켤레 전치가 같은 복소수 정사각 행렬이다. 다시 말해, 임의의 $n\times n$행렬에 대해 아래의 성질이 성립한다면 에르메트 행렬이다.

\[A^H=A\]

즉,

\[A_{ij}=\bar{A_{ji}}\]

여기서 $A^H$은 켤레 전치(conjugate transpose), $\bar{A}$는 켤레 복소수(complex conjugate)를 의미한다.

에르미트 행렬은 실수 행렬(real matrices)에서 사용되던 전치 행렬 (transpose matrix)을 복소수 체계에 까지 개념을 확장한 것이다.

가령, 아래와 같은 행렬들이 에르미트 행렬이다.

\[\begin{bmatrix} 2 & 2+i & 4 \\ 2-i & 3 & i \\ 4 & -i & 1\end{bmatrix}\]

주요 성질

에르미트 행렬의 성질 중 중요한 성질 몇 가지만 꼽으면 아래와 같다.

1. 에르미트 행렬의 대각 원소는 항상 실수이다.

증명:

행렬 $A$가 $n\times n$에르미트 행렬이라고 할 때, $i = 1, 2, \cdots, n$에 대해서,

\[A_{ii}=\bar{A_{ii}}\]

이므로, $A_{ii}$의 허수부는 0이다.

2. 에르메트 행렬의 고윳값은 항상 실수(real number)이다.

증명:

$\lambda \in \Bbb{C}$가 에르미트 행렬 $A$의 고윳값이라고 하자. 그러면,

\[Av=\lambda v\]

인 고유벡터 $v\neq 0$가 존재한다고 할 수 있는 것이다. 그러면 여기서 $Av$에 $v$ 벡터를 한번 더 내적해보자. 내적 연산을 $\langle \cdot, \cdot \rangle$이라고 쓰면,

\[\langle Av, v\rangle=(Av)^Hv=v^HA^Hv=\langle v, A^Hv\rangle=\langle v, Av \rangle\]

과 같이 쓸 수 있다. 여기서 고윳값, 고유벡터의 정의에 의해 $Av=\lambda v$이므로 위 식의 가장 왼쪽에 있는 식은

\[\langle Av, v\rangle = \langle \lambda v, v\rangle=\bar \lambda v^Hv\]

이고,

위 식의 가장 오른쪽에 있는 식은

\[\langle v, Av\rangle=v^H\lambda v=\lambda v^Hv\]

이다. 한편, 고유벡터는 0벡터가 아니므로 $v^Hv$는 0이 아니다.

따라서,

\[\lambda = \bar\lambda\]

이므로 항상 고윳값 $\lambda$는 실수이다.

3. 에르미트 행렬의 서로 다른 고윳값에 대응하는 고유벡터들은 서로 직교한다.

증명:

0 벡터가 아닌 $n$ 차원 복소 벡터 $v_1, v_2\in \Bbb{C}^n$가 행렬 $A$의 고윳값 $\lambda_1\neq \lambda_2$에 대한 고유벡터라고 하자. 이제 $Av_1$이라는 벡터에 $v_2$ 벡터를 내적해보자. 그러면,

\[\langle Av_1, v_2\rangle=(Av_1)^Hv_2=v_1^HA^Hv_2=\langle v_1, A^Hv_2\rangle=\langle v_1, Av_2\rangle\]

과 같이 쓸 수 있다.

이 때, 위 식의 가장 왼쪽에 있는 식은

\[\langle Av_1, v_2\rangle = \langle \lambda_1v_1, v_2\rangle=\lambda_1\langle v_1, v_2\rangle\]

이며, 가장 오른쪽에 있는 식은

\[\langle v_1, Av_2\rangle=\langle v_1, \lambda_2 v_2\rangle=\lambda\langle v_1, v_2\rangle\]

이다.

두 식은 동일하므로

\[\lambda_1\langle v_1, v_2\rangle = \lambda_2\langle v_1, v_2\rangle\] \[\Rightarrow (\lambda_1-\lambda_2)\langle v_1, v_2\rangle = 0\]

이다.

여기서 $\lambda_1 \neq \lambda_2$이므로 $\langle v_1, v_2\rangle = 0$이다.

따라서, 서로 다른 두 고윳값에 대응되는 두 고유벡터는 서로 직교한다.

(P.S.)¹

여기서 만약 에르미트 행렬의 두 교윳값이 같다고 했을 때는 어떻게 대처할 수 있을까?

두 고윳값이 같은 에르미트 행렬 중 하나는 단위 행렬이다.

아래와 같은 행렬을 생각해볼 때,

\[\begin{bmatrix}1 & 0\\0 & 1\end{bmatrix}\]

고윳값은 두 개가 모두 1인데 고유벡터는 어느 방향의 벡터여도 상관없다는 것을 알 수 있다. 이러한 내용을 일반화 하면 다음과 같이 생각할 수 있다.

만약, 두 고윳값이 같다고 하면 선형독립인 두 벡터 $v_1$과 $v_2$를 정하고 이 두 벡터가 생성하는 벡터 공간 안에 있는 벡터를 두 개 선택하면 된다.

다시 말해, 임의의 행렬 $A$에 대해서,

\[A(av_1+bv_2)=a Av_1+bAv_2 = a\lambda v_1 + b\lambda v_2 = \lambda(av_1 + bv_2)\]

따라서, $av_1+bv_2$와 같이 $v_1$과 $v_2$가 span하는 벡터 공간안에서 임의의 벡터 두 개를 선정할 수 있으며 꼭 직교해야 하는 것은 아니지만 직교하는 벡터 두 개를 선정할 수 있음을 알 수 있다.

고유벡터를 이용한 해(solution)의 표현

$A$가 $n\times n$ 에르미트 행렬이라고 하고,

\[Ax_i=\lambda_i x_i \quad\text{ for }\quad i=1,2,\cdots,n\]

와 같은 $n$개의 eigenvalue $\lambda_i$와 eigenvector $x_i$를 생각해보자.

$n\times n$ 에르미트 행렬은 고윳값이 distinct 하다고 하면 서로 직교하는 고유벡터 $n$개를 갖는다.

따라서, $n$ 차원 복소공간의 어떤 벡터라도 eigenvector의 선형결합으로 표현할 수 있게 된다.

그러므로 $Ax=b$ 문제를 풀고자 할 때 solution $x$는 다음과 같이 표현할 수도 있는 것이다.

\[x=\sum_{i=1}^{n}c_i x_i\]

즉, 우리는 solution $x$를 고유벡터 이용해 표현할 수 있으며, 우리가 알아야 하는 것은 기저벡터를 얼마만큼 써먹을 것인지에 관한 $c_i$ 값이다.

고유벡터 $x_i$와 $Ax=b$의 $b$ 벡터는 모두 알고 있는 것이므로 다음과 같이 $c_i$ 값을 구할 수 있게 된다.

아래와 같은 수식에 대해서,

\[Ax=b\]

$x$를 고유벡터를 이용해 표현해주면 다음과 같이 쓸 수 있다.

\[A\sum_{i=1}^n c_ix_i=b\]

여기서 양변에 다시 고유벡터 $x_j$와 내적을 취해주자.

\[A\sum_{i=1}^n c_ix_i\cdot x_j=b\cdot x_j\]

여기서 좌변에 있던 $A$를 summation 안에 넣어줘서,

\[\sum_{i=1}^n c_iAx_i\cdot x_j=b\cdot x_j\]

와 같이 만들면 고윳값, 고유벡터의 정의에 의해 아래와 같이 식을 바꿔 쓸 수 있다.

\[\Rightarrow \sum_{i=1}^n c_i\lambda_i x_i\cdot x_j=b\cdot x_j\]

$A$는 에르미트 행렬이라고 하고 만약 모든 eigenvalue들이 distinct하다면 서로 다른 eigenvector들은 서로 직교이다.

따라서, 위 식의 $x_i\cdot x_j$는 $i=j$인 경우에만 1이고 아닌 경우에는 0이 된다. 따라서,

\[\Rightarrow c_j\lambda_j (x_j\cdot x_j) = b\cdot x_j\] \[=c_j\lambda_j=b\cdot x_j\]

그러므로 $c_i$는 다음과 같이 계산할 수 있는 것이다.

\[c_i = \frac{b\cdot x_i}{\lambda_i}\]

그렇기 때문에, 일반적으로 $Ax=b$ 문제에 대한 솔루션은 eigenvector, eigenvalue를 이용해 다음과 같이 쓸 수도 있는 것이다.

\[x=\sum_{i=1}^{n}c_ix_i=\sum_{i=1}^{n}\left(\frac{b\cdot x_i}{\lambda_i}\right)x_i\]

흥미로운 점은 이런 방식으로 솔루션을 얻으면 꼭 inverse를 구하지 않고도 해를 구할 수 있다는 점이다.

고유함수 전개

고윳값, 고유함수의 개념 소개

선형대수학에서 $Ax=b$ 문제를 풀 때 고유벡터를 기저로 solution $x$를 표현함으로써 solution을 구해냈다면 함수해석학에서도 마찬가지로 $Lu=f$ 문제를 풀 때 solution function $u$를 고유함수를 기저로 표현함으로써 문제를 풀 수도 있다.

선형연산자 $L$에 대해 고윳값 $\lambda_n$과 고유함수 $u_n$의 개념을 생각해보자.

이전 선형 연산자와 함수 공간 편에서 보았던 것 처럼 행렬이 벡터를 입력받고 벡터를 출력해주는 함수로 작용하듯이,

어떤 함수를 입력받고 새로운 함수를 출력해주는 새로운 개념의 함수를 생각해볼 수 있다. 이 때, 이 입출력 함수간의 관계를 매개해주는 것이 선형 연산자라고 언급하였다.

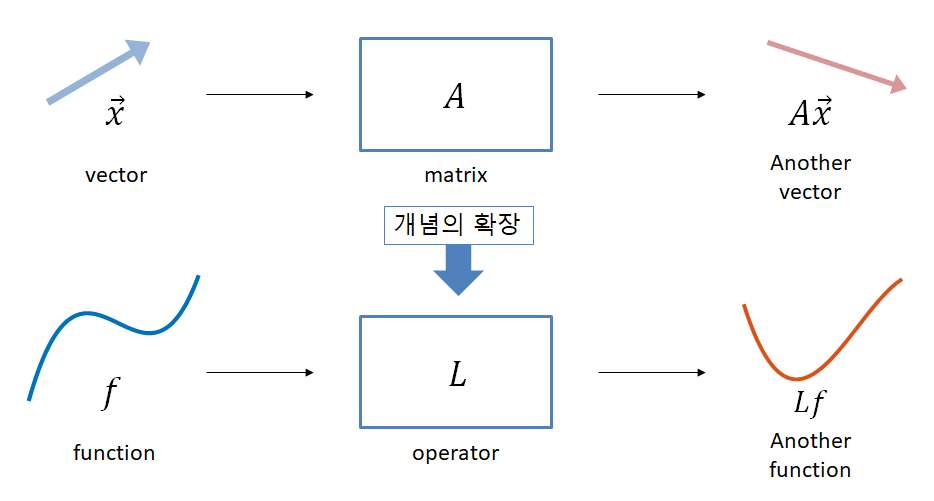
그림 1. 벡터와 행렬의 관계는 함수와 연산자의 관계로 개념이 확장된다.

한편, 선형대수학에서는 고윳값과 고유벡터를 정의했는데, 이 개념은 어떤 벡터에 행렬을 적용할 때 행렬을 통해 출력된 벡터가 입력된 벡터의 상수배이기만 한 벡터를 찾을 수 있다면 그 벡터가 고유벡터, 그 상수배된 상수값이 고윳값임을 말해준 것이었다.

이 개념을 확장시키면 선형 연산자도 고윳값, 고유함수의 개념을 생각할 수 있다는 것을 알 수 있다.

다시 말해 아래와 같은 관계를 가지는 함수 $u_n$과 $\lambda_n$을 생각해낼 수 있다.

\[Lu_n=\lambda_n u_n \quad\text{for}\quad n = 1, 2, \cdots, \infty\]

위 식이 말해주는 것은 $L$이라는 선형연산자를 $u_n$이라는 함수에 적용해주면 그 특정 $u_n$이라는 함수는 입력함수의 $\lambda_n$ 배만큼만 변하게 만들어준다는 뜻이다.

직교하는 고유함수를 이용한 전개

이 포스팅의 초반부에서 eigenvector의 선형 결합을 이용해 해를 표현할 수 있었던 것 처럼 eigenfunction의 선형 결합을 이용해 $Lu=f$의 해를 표현할 수 있다.

아래와 같은 미분방정식을 생각하자.

\[Lu=f\]

여기서 연산자 $L$이 서로 직교하는 무한개의 고유함수 $u_n \quad\text{for}\quad n = 1, 2, \cdots \infty$를 갖는다고 가정하자². 그리고 이 고유함수들의 크기(norm)는 모두 1이라고 가정하자.

그러면 $Lu=f$의 솔루션 함수 $u$ 는 고유함수 $u_n$을 새로운 기저로하여 다음과 같이 표현할 수 있다.

\[u(x)=\sum_{n=1}^{\infty}c_n u_n\]

이를 고유함수 전개(eigenfunction expansion)이라고 한다.

한편, 구간 $[a, b]$에서 정의된 두 함수 간의 내적 연산을 아래와 같이 정의하자.

\[\langle f, g\rangle=\int_{a}^{b}f^*(x)g(x) dx\]

여기서 $^*$은 complex conjugate을 표시한 것이다.

그리고 함수의 크기(norm)은 내적을 이용해 다음과 같이 정의하자.

\[\text{norm}(f)=\sqrt{\langle f,f\rangle}\]

이제 $Lu=f$라는 식을 다음과 같이 고유함수를 이용해 풀어 써보자.

\[Lu=L\sum_{n=1}^{\infty}c_nu_n=f\]

그리고 위 식의 양변에 고유함수 $u_m$을 내적해주면,

\[\Rightarrow \langle L\sum_{n=1}^{\infty}c_n u_n, u_m\rangle=\langle f, u_m\rangle\]

연산자 $L$은 선형연산자이므로 아래와 같이 summation 안으로 $L$을 넣어주자.

\[\Rightarrow \langle \sum_{n=1}^{\infty}c_nLu_n, u_m \rangle = \langle f, u_m \rangle\]

고윳값과 고유함수의 정의에 따라 다음과 같이 식을 바꿀 수 있다.

\[\Rightarrow \langle\sum_{n=1}^{\infty}c_n\lambda_n u_n, u_m\rangle=\langle f,u_m\rangle\]

여기서 모든 서로 다른 고유함수들은 직교한다고 하였으므로, $u_n$과 $u_m$ 같을 때만 $\langle u_n, u_m\rangle$이 1이고 아닐 때는 모두 값이 0이 된다. 따라서,

\[\Rightarrow c_m\lambda_m=\langle f, u_m\rangle\]

그러므로, $u(x)$를 고유함수 전개하기 위해 필요한 계수 $c_n$을 구하였다고 할 수 있다. 따라서, $u(x)$에 대한 고유함수 전개는 다음과 같다.

\[u(x)=\sum_{n=1}^{\infty}c_n u_n=\sum_{n=1}^{\infty}\frac{\langle f,u_n\rangle}{\lambda_n}u_n\]

예제 문제

아래와 같은 경계값 문제에 대해 고유함수 전개를 수행해보자.

\[-\frac{d^2}{dx^2}u(x)=f(x)\quad u(0)=0, u(l)=0\]

풀이

우리는 위 문제를 $Lu=f$의 문제로 생각해본다면 연산자 $L$은

\[L=-\frac{d^2}{dx^2}\]

과 같다는 것을 알 수 있다.

따라서, 이 연산자에 대한 고윳값 문제를 풀기 위해 다음과 같은 식을 생각해보자.

\[Lu=\lambda u\] \[\Rightarrow -\frac{d^2}{dx^2}u=\lambda u\] \[\Rightarrow \frac{d^2}{dx^2}u+\lambda u = 0\]

이 식은 일반적인 2계 상미분방정식이므로 솔루션은,

\[u=c_1\sin{\sqrt{\lambda}}x+c_2\cos{\sqrt{\lambda}}x\]

이다. 여기서 Boundary Condition을 적용해보면,

\[u(0) = c_2\cos(0)=0\] \[\therefore c_2 = 0\] \[u(l)=c_1\sin\sqrt{\lambda}x=0\]

여기서 중요한 부분은 $c_1$을 0으로 만들어버리면 솔루션이 $u(x)=0$이 되어버리므로 trivial solution을 구하는 것이 된다. 따라서, trivial solution이 나오지 않도록 막기 위해선 고윳값을 다음과 같이 정해야 함을 알 수 있다.

\[\sqrt\lambda =\frac{n\pi}{l}\]

따라서, 고유함수들은

\[u_n=\left\lbrace\sin\frac{n\pi x}{l}\right\rbrace\quad\text{for }n\in\Bbb{N}\]

가 된다. 그런데 이 고유함수들의 크기(norm)는 1이 아니기 때문에 정규화를 시켜줘서 크기가 1인 고유벡터들로 모두 수정하자.

각 고유함수들의 크기는

\[\sqrt{\int_{0}^{l}\sin\left(\frac{n\pi x}{l}\right)\sin\left(\frac{n\pi x}{l}\right)dx}=\sqrt{\frac{l}{2}}\]

이다. 따라서, 정규화된 고유함수들은

\[u_n=\left\lbrace\sqrt{\frac{2}{l}}\sin\frac{n\pi x}{l}\right\rbrace\quad\text{for }n\in\Bbb{N}\]

과 같다.

이 고유함수들은 직교한다는 것을 함수의 내적을 통해서 쉽게 확인할 수 있다.

\[\langle u_n, u_m\rangle=\int_{0}^{l}\left(\sqrt{\frac{2}{l}}\sin\frac{n\pi x}{l}\right)\left(\sqrt{\frac{2}{l}}\sin\frac{m\pi x}{l}\right)dx\] \[=\int_{0}^{l}\frac{l}{2}\sin\left(\frac{n\pi x}{l}\right)\sin\left(\frac{m\pi x}{l}\right)dx\] \[=\begin{cases}0 & m\neq n\\ 1 &m=n\end{cases}\]

그러므로 원래 문제의 조건을 만족하는 해 $u(x)$ 는 아래와 같이 고유함수 전개해서 표현할 수 있다.

\[u(x)=\sum_{n=1}^{\infty}c_n\sqrt\frac{2}{l}\sin\left(\frac{n\pi x}{l}\right)\] \[c_n = \frac{\langle f, u_n\rangle}{\lambda_n}\]

만약 $f(x) = x$이라고 하고, $l=1$이라고 하면,

\[c_n =\frac{1}{(n\pi)^2}\int_{0}^{1}(x)\sqrt{2}\sin\left(n\pi x\right)dx\] \[=\frac{\sqrt{2}}{n^2\pi^2}\int_{0}^{1}x\sin(n\pi x)dx\]

부분적분을 활용하면 다음과 같이 쓸 수 있다.

\[\Rightarrow \frac{\sqrt{2}}{n^2\pi^2}\left(x\cdot\frac{-1}{n\pi}\cos(n\pi x)\right)\Big|_{0}^{1}-\int_{0}^{1}\left(\frac{-1}{n\pi}\right)\cos(n\pi x)dx\] \[=\frac{\sqrt{2}}{n^2\pi^2}\cdot\left(\frac{-1}{n\pi}\right)\cos(n\pi)\] \[=(-\sqrt{2})\frac{(-1)^n}{n^3\pi^3}\]

이므로,

\[u(x) = \sum_{n=1}^{\infty}c_n\sqrt\frac{2}{l}\sin\left(\frac{n\pi x}{l}\right)=\sum_{n=1}^{\infty}(-\sqrt{2})\frac{(-1)^n}{n^3\pi^3}\sqrt{2}\sin(n\pi x)\]

와 같다는 것이다.

이 미분방정식을 다시 쓰면

\[-\frac{d^2u}{dx^2}=x\]

이고 경계조건은 $u(0)=0$, $u(1)=0$이다. 이 방정식의 해를 eigenfunction expansion이 아닌 일반적인 방법으로 직접 구해보면

\[u(x) = \frac{x(1-x^2)}{6}\]

임을 쉽게 알 수 있는데, 위의 eigenfunction expansion으로 구한 식을 $n$이 1일 때부터 서서히 더해나가면 일반적인 방법으로 구한 해에 근사해 가는 것을 확인할 수 있다.