스토크스의 정리

스토크스 정리의 수식

스토크스 정리의 수식을 써보자면 다음과 같다.

\[\oint_c\vec{F}\cdot d\vec{r} = \iint_S(\vec{\nabla}\times\vec{F})\cdot d\vec{S}\]

식 (1)을 놓고 잘 생각해보면 그린정리의 수식과 매우 유사하다는 것을 알 수 있다. 그린정리의 수식은 다음과 같았다.

\[\oint_c\vec{F}\cdot d\vec{r} = \iint_A(\vec{\nabla}\times\vec{F})_{2D} dA\]

여기서 $(\vec{\nabla}\times\vec{F})_{2D}$는 2D curl이라는 의미로, 수식은 curl의 수식과 같으나 2차원에서 더 이상 $\hat k$방향으로 표시할 벡터가 없어 curl의 크기만 사용하겠다는 의미이다.

식 (1)과 식 (2)를 비교해보면 그린 정리는 선적분과 중적분 간의 관계에 대해 설명해주고 있는 반면, 스토크스 정리는 선적분과 면적분 간의 관계에 대해 설명해주고 있다고 할 수 있다.

스토크스의 정리는 그린 정리의 3차원 버전이라고 할 수 있다. 일반적인 스토크스 정리는 더 고차원 다양체에 대해 다룰 수 있다고 하지만, 우리는 우리가 필요한 3차원 정도의 수준에서 이해와 증명을 해보도록 하자.

스토크스 정리의 의미

prerequisites

스토크스 정리의 의미를 이해하기 위해선 다음의 내용에 대해 알고 오는 것이 좋습니다

특히, 그린 정리의 의미 설명 부분에 대해서는 꼭 알고 오시는 것을 추천드립니다.

스토크스 정리의 의미 소개

아래와 같이 어떤 벡터장 위에 넓이를 갖는 곡면 S과 그 가장 외각의 폐곡선 C가 있다고 하자.

그림 1. 3차원 공간 위에 임의의 곡면 S와 폐곡선 C를 가정해보자.

이 때, 이 3차원 공간에 벡터장 $\vec{F}$가 주어져 있다고 하면 스토크스 정리에 의해 아래의 식이 성립한다.

\[\oint_C\vec{F}\cdot d\vec{r} = \iint_S(\vec{\nabla}\times\vec{F})\cdot d \vec{S}\]

식 (3)의 좌변은 curve C를 따라 벡터장에 대해 선적분한 것이다.

이제 식 (3)의 좌변으로부터 식(3)의 우변을 유도해보자. 곡면 $S$를 아래와 같이 반으로 쪼개서 보도록 하자.

그림 2. 곡면 S를 두 개의 페곡선으로 나누어 표현한 것.

위 그림 2를 위쪽에서 조감해보면 아래와 같다.

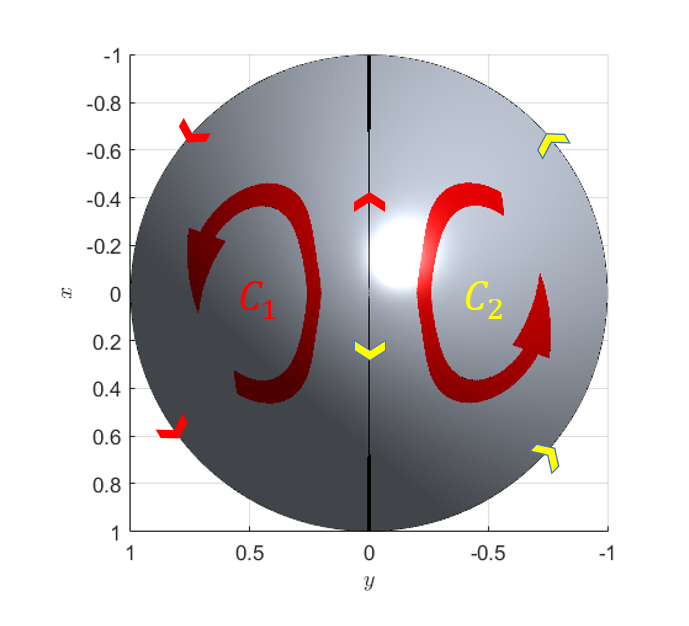
그림 3. 곡면 S를 2개의 폐곡선으로 나누었을 때의 선적분 경로

그림 3에서 보면 두 개로 쪼개진 닫힌 경로를 각각 $C_1$, $C_2$라고 하였다.

또한, $C_1$과 $C_2$의 선적분 경로를 잘 생각해보면 가운데 있는 구간에서는 선적분 경로의 길이는 같으나 길이는 반대이므로 이 영역에서는 선적분의 값이 상쇄된다.

따라서, 우리는 다음과 같은 관계를 생각할 수 있다.

\[\oint_C\vec{F}\cdot d\vec{r} = \oint_{C_1}\vec{F}\cdot d\vec{r} + \oint_{C_2}\vec{F}\cdot d\vec{r}\]

이번엔 아래와 같이 곡면 $S$를 4등분 해보자.

그림 4. 곡면 S를 네 개의 페곡선으로 나누어 표현한 것.

위 그림 4를 위쪽에서 조감해보면 아래와 같다.

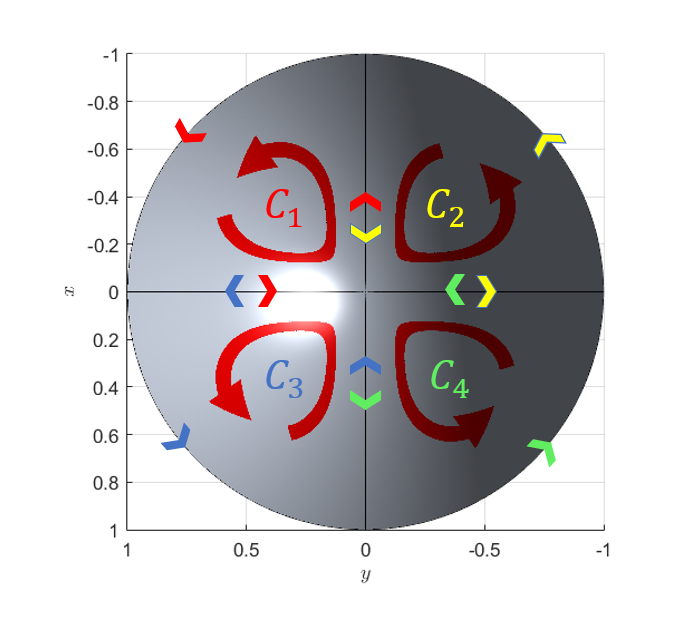
그림 5. 곡면 S를 2개의 폐곡선으로 나누었을 때의 선적분 경로

앞서 곡면을 두 개로 쪼갰을 때와 마찬가지의 논리로 내부의 경로에서는 선적분 시 길이는 같고 방향은 반대이므로 $C_1$에서 $C_4$까지의 네 개의 닫힌 경로에 대한 선적분을 모두 더해주면 기존의 최외각 경로에 대한 선적분의 값과 같아진다.

\[\oint_C\vec{F}\cdot d\vec{r} = \sum_{k=1}^4\oint_{C_k}\vec{F}\cdot d\vec{r}\]

그렇다면 곡면 $S$를 $N$ 등분하면 어떻게 될까?

그림 6. 곡면 S를 많은 페곡선으로 나누어 표현한 것.

지금까지의 논리와 같이 아무리 많은 폐곡선으로 쪼개더라도 아래의 식이 성립하게 된다.

\[\oint_C\vec{F}\cdot d\vec{r} = \sum_{k=1}^N\oint_{C_k}\vec{F}\cdot d\vec{r}\]

이 때, $N$ 개로 쪼깨진 작은 곡면을 생각해보면 아래와 같이 상상할 수 있는데, 이 작은 경로 내부의 선적분은 결국 미소 경로에서의 벡터장의 회전과 같은 의미를 갖게 된다.

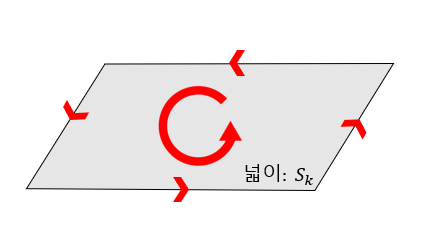
그림 7. 작은 곡면에서의 경로와 선적분

또, curl 편에서 확인했던 것 처럼 curl은 단위 영역에서 받는 회전력이므로 넓이가 $dS$인 곡면에서의 회전량은 curl의 값에 곡면의 넓이를 곱해준 값으로 생각할 수 있다.

한편 curl의 벡터 방향과 곡면의 법선 벡터는 방향이 같으므로 curl의 크기와 곡면의 넓이의 곱은 curl 벡터와 곡면의 면벡터의 내적과 같다고 볼 수 있다.

그러므로, 아래와 같이 생각할 수 있다.

\[\oint_{C_k}\vec{F}\cdot d\vec{r}\approx(\vec\nabla\times\vec F)_{C_k}\cdot \vec{S}_k\]

따라서 식 (6)을 다시 쓰면 아래와 같다.

\[식(6) = \sum_{k=1}^N\oint_{C_k}\vec{F}\cdot d\vec{r} \approx \sum_{k=1}^N(\vec\nabla\times\vec F)_{C_k}\cdot \vec{S}_k\]

식 (8)에서 $N$을 무한히 크게 만들면 $\vec{S}_k$는 $d\vec{S}$가 될 것이고 결국 식 (6)은 다음과 같이 변하게 될 것이다.

\[\oint_C\vec{F}\cdot d\vec{r} = \iint_S(\vec{\nabla}\times\vec{F})\cdot d\vec{S}\]

이렇듯 스토크스 정리는 곡면의 모양이 어떠하든 간에 상관없이 닫힌 경로의 모양만 유지된다면 같은 결과값을 가져오게 된다.

그림 8. 곡면 S의 모양이 어떻든 간에 상관없이 닫힌 경로 C의 모양만 유지된다면 스토크스 정리는 항상 성립한다.

스토크스 정리의 증명

prerequisites

스토크스 정리의 증명 과정을 잘 이해하기 위해선 다음의 네 가지 정도의 내용에 대해서는 알고 오시는 것이 좋습니다.

여기서 필요한 편미분의 chain rule은 다음과 같이 세 가지이다.

1) for a function $f(x, y, g(x,y))$

\[\frac{\partial}{\partial x}f(x,y,g(x,y)) = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial g}\frac{\partial g}{\partial x}\]

2) for two functions $f(x, y, z)$ and $h(x,y,z)$

\[\frac{\partial}{\partial x}(f\cdot h) = \frac{\partial f}{\partial x}h + f \frac{\partial h}{\partial x}\]

3) for a function $f(x(t), y(t))$

\[\frac{df}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}\]

위 세 가지 chain rule들은 증명 과정 이곳 저곳에서 필요할 때 쓰일 것이므로 혹시 어려운 부분이 있다면 미리 숙지해두도록 하자.

증명을 위한 곡면과 정의역 소개

이번 증명 과정에서는 정의역이 $x$, $y$ 평면이고 높이가 $z=g(x,y)$와 같이 정해지는 함수를 통해 스토크스 정리를 증명하고자 한다.

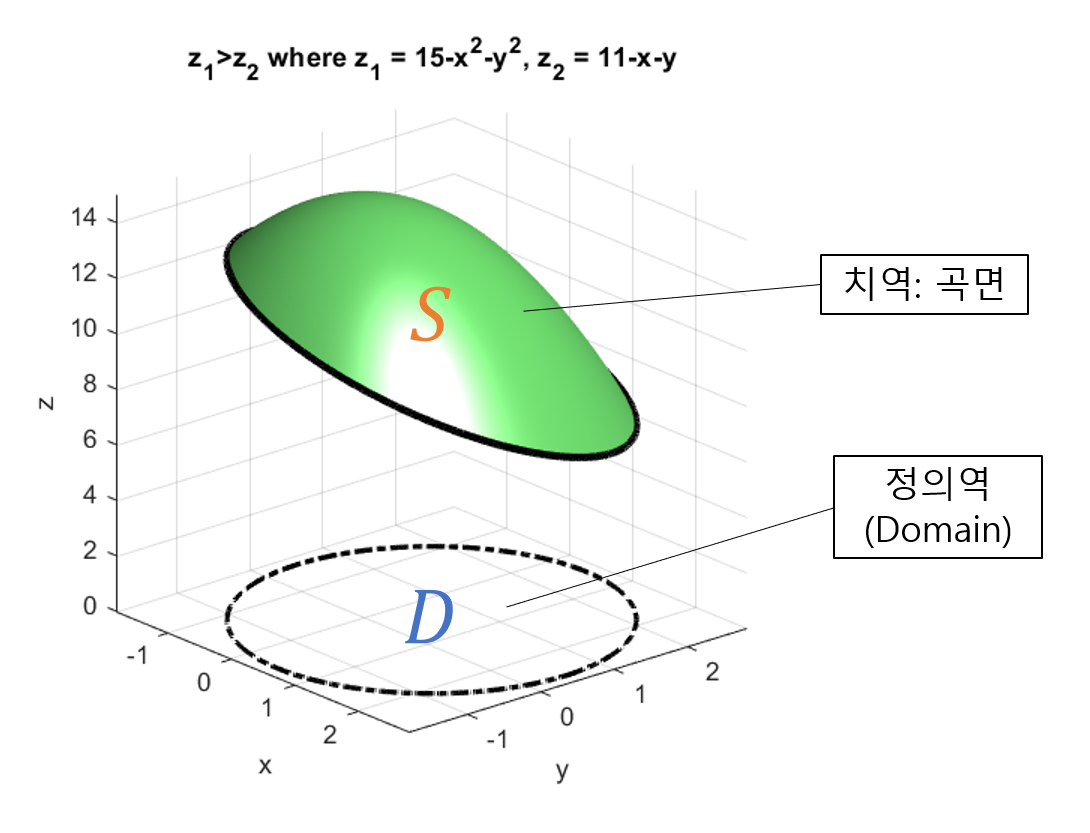
그림 9. 스토크스 정리의 증명을 위한 정의역이 x, y이고 높이가 x, y의 함수로 정해지는 영역과 닫힌 경로(검은 실선)와 그 정사영(점선 표시)

이후 정의역이 $x$, $z$인 경우와 $y$, $z$인 경우에 대해서는 지금의 정의역이 $x$, $y$인 경우에 대한 증명 방식과 유사한 방식으로 증명할 수 있다는 방식으로 일반적인 3차원 공간에 대해 스토크스 정리를 증명할 수 있다.

여기서 3차원 공간상에 주어진 벡터 필드 $\vec{F}$를 $\lt P, Q, R\gt$로 쓰도록 하자. 꺽쇠 괄호로 표시한 것은 원래의 $\vec{F} = P(x,y,z)\hat i +Q(x,y,z)\hat j + R(x,y,z)\hat k$를 줄여 표시한 것이다.

스토크스 정리의 수식을 쓰면 다음과 같이 쓸 수 있다.

\[\oint_c\vec{F}\cdot d\vec{r} = \iint_S(\vec{\nabla}\times\vec{F})\cdot d\vec{S}\]

면적분 부분의 계산

여기서 우리는 면적분 부분 증명을 먼저 시작해보자.

\[\iint_S(\vec{\nabla}\times\vec{F})\cdot d\vec{S}\]

여기서 벡터장의 curl 부분만 따로 계산해도록 하자.

\[\vec{\nabla}\times\vec{F} = \begin{vmatrix} \hat{i} && \hat{j} && \hat{k} \\ \frac{\partial}{\partial x} && \frac{\partial}{\partial y} && \frac{\partial}{\partial z} \\ P && Q && R \end{vmatrix}\] \[=\lt R_y-Q_z, P_z- R_x, Q_x - P_y \gt\]

여기서 $R_y$등의 표기는 $R$에 대한 $y$의 편미분으로 생각하면 된다.

또, 면벡터 $d\vec{S}$에 대해 생각해보면 매개 변수 2개를 이용해 곡면을 나타내는 일반적인 식은 아래와 같은데,

\[\vec{r}(u,v) = x(u,v)\hat{i} + y(u,v)\hat{j} + z(u,v)\hat{k}\]

이번 경우에는 매개변수 2개가 $x$와 $y$에 해당하므로 곡면의 방정식은 다음과 같이 나타낼 수 있다.

\[\vec{r}(x,y) = x\hat{i} + y\hat{j} + z\hat{j} = x\hat{i} + y\hat{j} + g(x,y)\hat{k} = \lt x, y, g(x,y)\gt\]

따라서, 벡터장의 면적분에서 알아보았던 것 처럼 면벡터 $d\vec{S}$는 아래와 같다.

\[d\vec{S} = \vec{r}_x\times\vec{r}_y dxdy = \begin{vmatrix}\hat{i} && \hat{j} && \hat{k} \\ 1 && 0 && g_x \\ 0 && 1 && g_y\end{vmatrix}dxdy\] \[=\lt -g_x, -g_y, 1\gt\]

따라서 식(14)는 다음과 같이 쓸 수 있다.

\[식(14)\Rightarrow \iint_S \lt R_y-Qz, P_z-R_x, Q_x-P_y\gt\cdot\lt -g_x, -g_y, 1\gt dxdy\] \[=\iint_D \left( g_x(Q_z-R_y) + g_y(R_x - P_z) + Q_x-P_y\right) dxdy\]

여기서 더 이상 해줄 수 있는 일이 없기 때문에 스토크스 정리 수식의 선적분 부분의 계산으로 넘어가도록 하자.

선적분 부분의 계산

\[\oint_C\vec{F}\cdot d\vec{r}\]

선적분 부분의 계산을 위해 아래의 그림 10과 같이 원래의 곡면에 대한 닫힌 경로를 $C$, 그 경로의 정의역으로의 정사영을 $C_0$라고 하자.

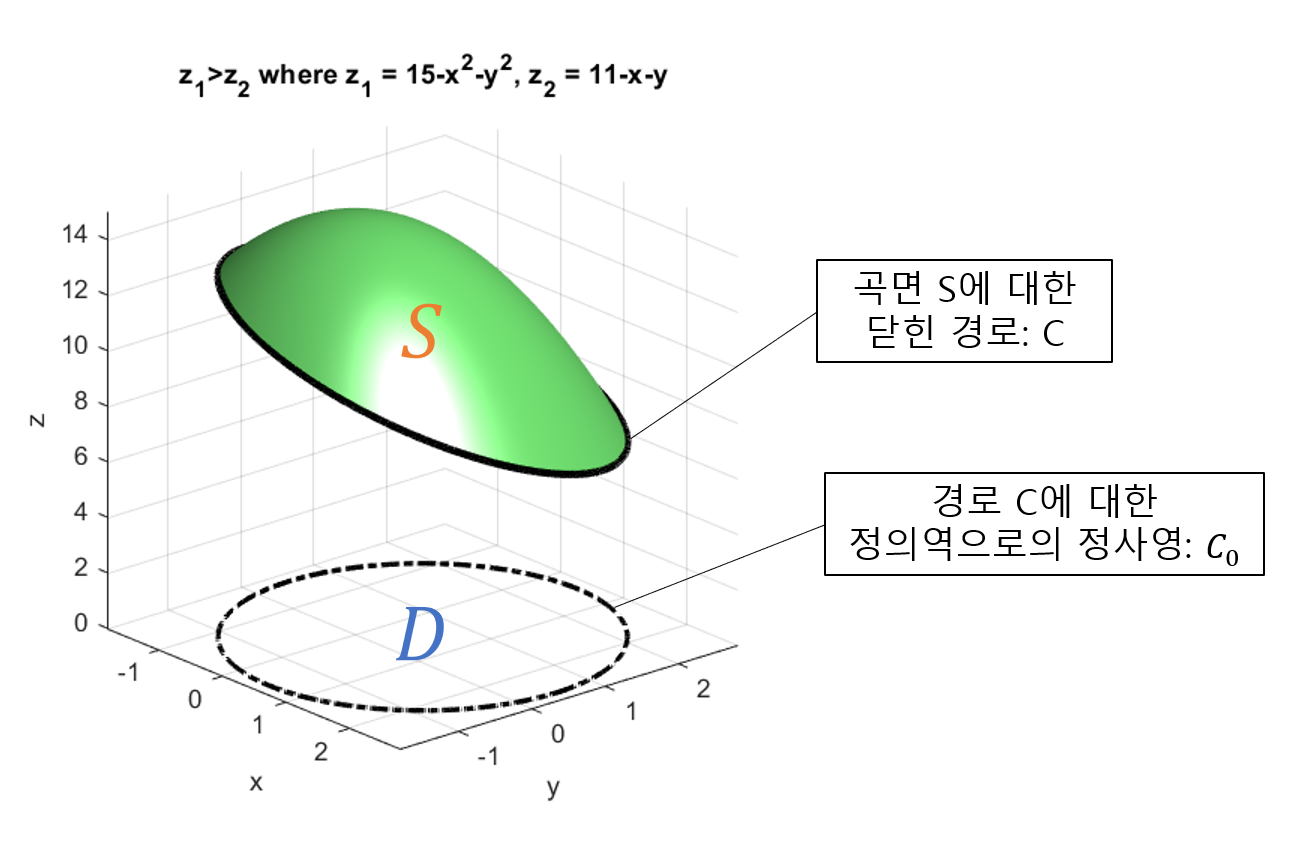
그림 10. 닫힌 경로 C와 그 경로의 정의역으로의 정사영 C_0

그러면 $C_0$에 대한 곡선의 매개변수 방정식은 다음과 같이 생각할 수 있다.

\[\vec{r}_{C_0} = \lt x(t), y(t)\gt\text{ where }a\leq t \leq b\]

또, 이에 따라 원래의 닫힌 경로 $C$에 대한 곡선의 매개변수 방정식은 다음과 같이 생각할 수 있다. 여기서 $a$와 $b$는 $a\lt b$인 임의의 실수이다.

\[\vec{r}_C = \lt x(t), y(t), g(x(t), y(t))\gt\text{ where }a\leq t \leq b\]

이제 우리는 닫힌 곡선 $C$에 대한 미소변위 $d\vec{r}$에 대해 생각해보자. 우선 $d\vec{r}$을 계산하기 위해 $r$을 $t$에 대해 먼저 미분해보자. 스토크스 정리의 증명 파트 초반부에 소개하였던 편미분 chain rule 3) (식 (12))를 적용해보면 아래와 같다.

\[\frac{d\vec{r}}{dt} = \lt \frac{dx}{dt}, \frac{dy}{dt}, g_x \frac{dx}{dt} + g_y \frac{dy}{dt}\gt\]

그런 다음 위 식에서 $dt$를 양변에 곱해주면,

\[d\vec{r} = \lt dx, dy, g_x dx + g_y dy\gt\]

따라서, 여기서 $\vec{F}$는 주어진 것이므로, $\vec{F}\cdot d\vec{r}$은 아래와 같다.

\[\vec{F}\cdot d\vec{r} = \lt P, Q, R \gt \cdot \lt dx, dy, g_x dx + g_y dy\gt = Pdx + Qdy + R g_x dx + Rg_y dy\]

이를 이용하면 원래의 식 (23)의 선적분은 $t$에 대한 적분으로 바꿀 수 있다.

\[식(23)\Rightarrow \int_{t=a}^{t=b}Pdx+Qdy+Rg_xdx+Rg_ydy\]

여기서 $dx$, $dy$에 대해 묶으면,

\[\Rightarrow \int_{t=a}^{t=b}(P+Rg_x)dx + (Q+Rg_y)dy\]

여기서 그린정리를 적용하면 2차원 평면 상의 닫힌 경로에 대한 선적분을 중적분으로 바꿔줄 수 있으므로,

\[\Rightarrow \iint_D(Q+Rg_y)_x - (P+Rg_x)_y dxdy\]

여기서 괄호 뒤에 있는 아래첨자 $x$, $y$는 각각 $x$에 대한 편미분과 $y$에 대한 편미분을 의미한다.

이제 식 (31)의 두 개의 편미분 계산을 각각 수행해보도록 하자.

(Q+Rg_y)_x에 대한 편미분 계산

식 (31)에서 앞쪽의 편미분 계산부를 먼저 가져오면,

\[(Q+Rg_y)_x = \frac{\partial}{\partial x}\left( Q(x, y, g(x,y)) + R(x, y, g(x,y))g_y(x, y) \right)\]

이 때, 증명부 초반에 소개했던 편미분 chain rule 중 첫 번째인 식 (10)과 두 번째인 식 (11)을 사용하면 위 식은 아래와 같이 쓸 수 있다.

\[\Rightarrow Q_x + Q_g g_x + (R_x+R_g g_x)g_y + Rg_{yx}\]

여기서 $Q_g$나 $R_g$나 $z=g(x,y)$이므로 각각 $Q_z$와 $R_z$로 쓸 수 있다.

\[\Rightarrow Q_x + Q_z g_x + (R_x+R_z g_x)g_y + Rg_{yx}\]

(P+Rg_x)_y에 대한 편미분 계산

식 (31)에서 뒷쪽의 편미분 계산부를 가져오면,

\[(P+Rg_x)_y = \frac{\partial}{\partial y}\left( P(x,y,g(x,y)) + R(x,y,g(x,y))g_x(x,y) \right)\]

이 때, 증명부 초반에 소개했던 편미분 chain rule 중 첫 번째인 식 (10)과 두 번째인 식 (11)을 사용하면 위 식은 아래와 같이 계산할 수 있다.

\[\Rightarrow P_y+P_z g_y + (R_y + R_z g_y)g_x + Rg_{xy}\]

두 편미분 계산 과정을 종합하면,

식 (31)을 계산하기 위해 식 (34)의 결과에서 식 (36)의 결과를 빼보도록 하자.

\[식(34)-식(36) = \left\lbrace Q_x+Q_zg_x+(R_x+R_zg_x)g_y +Rg_{yx}\right\rbrace \notag\] \[- \left\lbrace P_y+P_zg_y + (R_y+R_zg_y)g_x + Rg_{xy}\right\rbrace\] \[=Q_x-P_y + Q_xg_x-P_zg_y+R_xg_y-R_yg_x\] \[=g_x(Q_z-R_y) + g_y(R_x-P_z) + Q_x-P_y\]

따라서 식 (31)은 다음과 같다.

\[식(31) = \iint_D \left\lbrace g_x(Q_z-R_y) + g_y(R_x-P_z) + Q_x-P_y\right\rbrace dxdy\]