Interactive MCMC JS Applet by Chi-Feng, 소스코드
prerequisites
이 포스팅에 대해 잘 이해하기 위해선 다음의 내용에 대해 알고 오시는 것이 좋습니다.
MCMC의 정의
위키피디아에 따르면 마르코프 연쇄 몬테카를로 방법(Markov Chain Monte Carlo, MCMC)은 “마르코프 연쇄의 구성에 기반한 확률 분포로부터 원하는 분포의 정적 분포를 갖는 표본을 추출하는 알고리즘의 한 분류이다.”라고 나와있다.
복잡해보이지만 우선 MCMC는 샘플링 방법 중 하나인 것이라는 것만 알고있도록 하자. 언제나 그렇듯 정의만 보면 처음 볼 때는 이해할 수 있는 것이 거의 없기에 하나 하나 뜯어서 살펴볼 것이다.
이번 포스팅에서는 복잡한 수학적 내용을 전달하는 것 보다는 MCMC의 의미를 이해할 수 있도록하는데 초점을 맞추고자 한다.
Monte Carlo
Monte Carlo는 쉽게 말해 통계적인 수치를 얻기 위해 수행하는 ‘시뮬레이션’ 같은 것이다.
굳이 이런 시뮬레이션을 하는 이유는 통계학의 특성 상 무한히 많은 시도를 거쳐야만 진짜 정답이 뭔지 알 수 있지만, 그렇게 하기가 현실적으로 어렵기 때문에 유한한 시도만으로 정답을 추정하자는 데 의미가 있다.
Monte Carlo 방식의 시뮬레이션 중 가장 유명한 것 중 하나가 원의 넓이를 계산하는 시뮬레이션이다.
아래의 그림과 같이 가로, 세로의 길이가 2인 정사각형 안에 점을 무수히 많이 찍으면서, 중심으로부터의 거리가 1이하면 빨간색으로 칠하고, 그렇지 않으면 파란색으로 칠해준다.
전체적으로 찍은 점의 개수와 빨간색으로 찍힌 점의 개수의 비율을 계산하여 원래의 사각형의 면적인 4를 곱해주면 반지름이 1인 원의 넓이를 대략적으로 추정할 수 있다.
그림 1. 반지름이 1인 원의 넓이를 근사적으로 계산하는 Monte Carlo 시뮬레이션
MCMC에서는 “통계적인 특성을 이용해 무수히 뭔가를 많이 시도해본다”는 의미에서 Monte Carlo라는 이름을 붙였다고 보면 좋을 것 같다.
Markov Chain
Markov Chain은 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에만 영향을 받는 확률 과정을 의미한다.
이렇게 들으면 어렵게 들릴 수도 있겠지만, 다음과 같은 비유를 생각해보자.
보통 사람들은 전날 먹은 식사와 유사한 식사를 하지 않으려는 경향이 있다.
가령, 어제 짜장면을 먹었다면 오늘은 면종류의 음식을 먹으려고 하지 않는다.
이렇듯 음식 선택이라는 확률과정에 대해 오늘의 음식 선택이라는 과정은 어제의 음식 선택에만 영향을 받고, 그저께의 음식 선택에는 영향을 받지 않는다면
이 과정은 마르코프 성질(Markov property)을 가진다고 할 수 있으며, 이 확률 과정은 Markov chain이라고 할 수 있다.
앞서 MCMC는 샘플링 방법 중 하나라고 하였는데, “가장 마지막에 뽑힌 샘플이 다음번 샘플을 추천해준다”는 의미에서 Markov Chain이라는 단어가 들어갔다고 보면 좋을 것 같다.
MCMC를 이용한 샘플링
MCMC는 Monte Carlo와 Markov Chain의 개념을 합친 것이다.
다시 말해 MCMC를 수행한다는 것은 첫 샘플을 랜덤하게 선정한 뒤, 첫 샘플에 의해 그 다음번 샘플이 추천되는 방식의 시도를 무수하게 해본다는 의미를 갖고 있다.
위의 문장에서 가장 수학적이지 않은 단어는 뭘까? 바로 “추천”이다.
또, 추천 다음에는 “승낙/거절”의 단계까지도 포함되는데, 이 과정에 대해 알아보도록 하자.
참고로 이 post에서 주요하게 소개하는 MCMC 샘플링 알고리즘은 Metropolis 알고리즘이다.
샘플링 과정 (Metropolis 알고리즘)
우선은 Rejection Sampling을 할 때와 마찬가지로 샘플을 추출하고자 하는 target 분포가 하나 있어야 한다.
이 타겟 분포는 정확히는 확률밀도 함수가 아니어도 괜찮다. 대략적으로 확률밀도 함수의 크기에 비례하는 함수를 이용하면 충분하다.
가령 아래와 같은 함수를 타겟 분포로 사용할 수 있다.
\[f(x) = 0.3\exp\left(-0.2x^2\right) + 0.7\exp\left(-0.2(x-10)^2\right)\]이 함수는 $-\infty$부터 $\infty$까지의 전체 면적이 1이 아니기 때문에 확률밀도 함수라고 할수는 없다. 하지만, 만약 우리가 실험적인 결과로 확률밀도함수가 대략적으로 타겟 함수 $f(x)$와 비슷한 형태를 띄고 있다는 것을 알고 있다면 우리는 이러한 타겟 함수로부터 실제 확률밀도함수를 근사하기 위해 샘플링이 필요할 수 있다.
1. random initialization
MCMC의 샘플링 과정에서 가장 먼저 수행해줄 것은 random initialization이다.
쉽게 말해 샘플 공간에서 아무런 입력값이나 하나를 선택해 주는 것이다.
가령 아래의 그림과 같이 $x_0$를 임의로 선택할 수 있다.
아래 그림에서는 $x_0 = 7$로 설정해보았다.
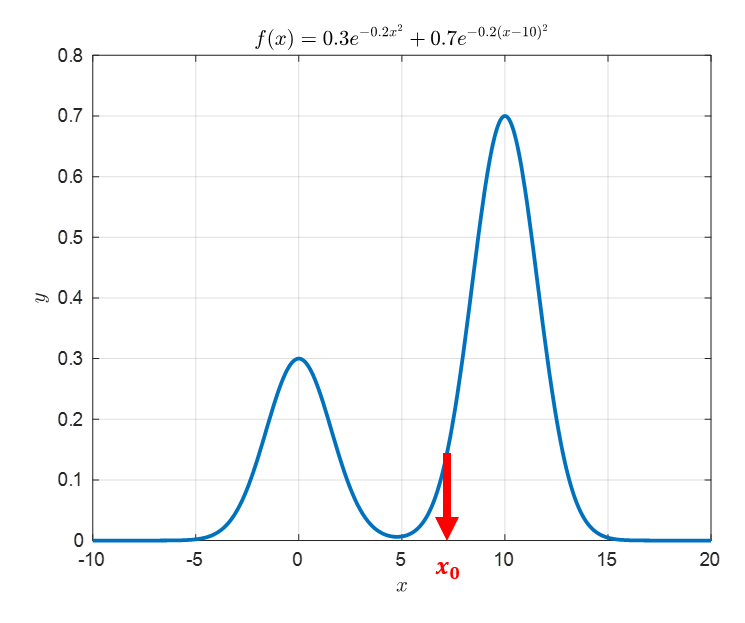
그림 2. target 분포와는 크게 관계없이 임의의 시작 포인트를 선택하여 MCMC 알고리즘을 시작한다.
2. 제안 분포로부터 다음 포인트를 추천받기
MCMC의 그 다음번 스텝은 제안 분포로부터 다음번으로 추출해볼 샘플을 추천받는 것이다.
제안분포는 어떤 확률분포를 이용해도 상관없으나, Metropolis는 symmetric한 확률분포를 사용하는 경우에 대한 알고리즘을 제안했고, Hastings는 일반적인 확률 분포에 대한 경우까지 어떻게 수학적으로 계산할 수 있는지에 관해 Metropolis가 제안한 알고리즘을 확장하였다.
우리는 논의를 쉽게 하기 위해서 symmetric한 확률분포를 제안분포로 사용해보도록 하자.
여기서 제안분포는 $g(x)$라고 부르도록 하자.
보통 symmetric한 제안분포로 많이 사용되는 확률분포는 예상했겠지만 정규분포이다.
그러면, 처음 시작으로 잡은 $x_0$를 중심으로 정규분포를 하나 그려본다.
이 때, 정규분포의 너비(즉, 표준 편차)는 연구자의 선택에 따라 임의로 설정하면 된다.
이번 그림에서는 표준편차를 2로 설정해보았다.
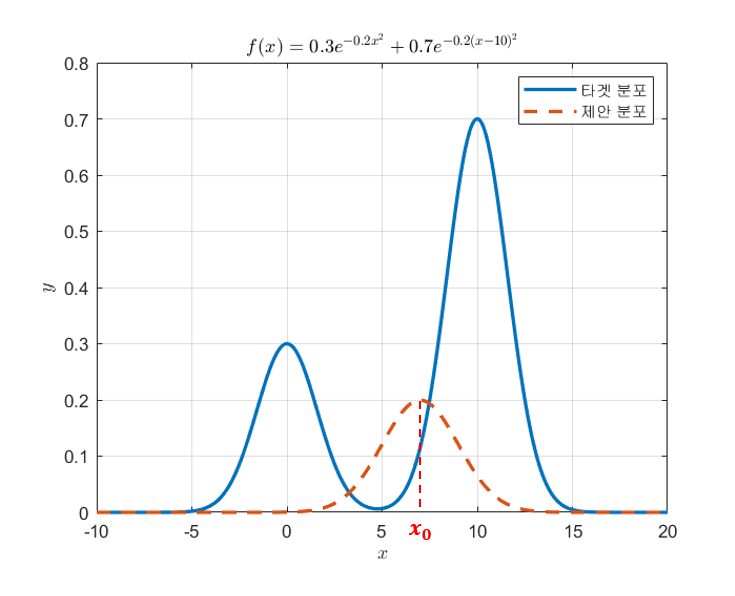
그림 3. 시작점에서 제안 분포를 형성하자.
잘 생각해보면 우리의 제안 분포는 정규분포인데 평균이 7이고 표준편차가 2이다.
이런 정규분포에서는 샘플을 추출하기가 쉽다. MATLAB에서는 randn()함수를 이용해서 쉽게 표본을 추출할 수 있다.
아래와 같이 제안 분포로부터 다음 포인트를 추천받아보자.
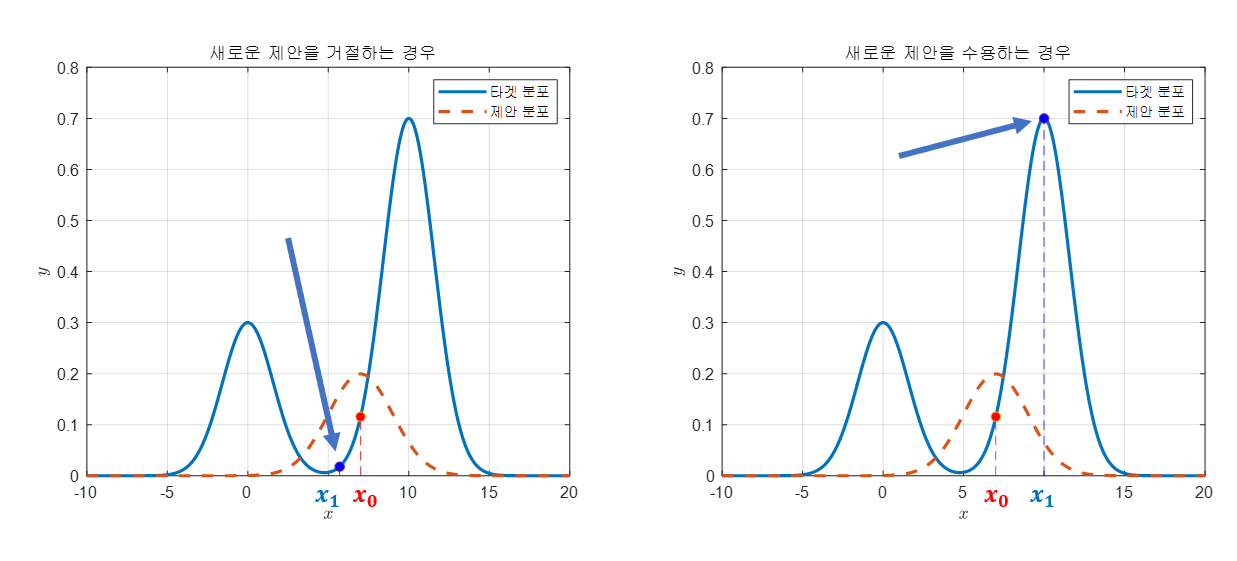
그림 4. 제안분포로부터 다음 포인트를 추천 받았을 때 어떤 경우는 추천을 거절하고, 어떤 경우는 추천을 수용한다.
그림 4를 보면 파란색 점으로 표시한 것들이 새롭게 제안된 샘플 포인트와 그 포인트에서의 타겟 분포의 값을 표현하였다.
또, 그림 4를 잘 보면 왼쪽 그림에서 제안된 새로운 샘플 포인트는 거절됐고, 오른쪽 그림에서 제안된 새로운 샘플 포인트는 수용되었다.
거절의 이유는 타겟 분포에서의 높이가 원래의 $x_0$에서의 높이보다 제안된 샘플 포인트의 타겟 분포의 높이보다 낮아서이고,
수용의 이유는 반대로 타겟 분포에서의 높이가 원래의 $x_0$에서의 높이보다 제안된 샘플 포인트의 타겟 분포에서의 높이보다 높아서이다.
즉, 다음의 기준에 따라 수용 여부를 결정한다.
\[\frac{f(x_1)}{f(x_0)}>1\]만약, 제안이 수용되었다면 수용된 샘플 포인트를 중심으로 제안 분포를 그리고 이를 통해 샘플을 또 추천받아본다.
그런데, 제안이 수용되지 않았다면 통계적으로 수용하게끔 MCMC는 패자부활전을 마련해놓았다.
3. 패자부활전
앞서 2번 단계에서 거절된 샘플들은 무조건 이용하지 않는 것은 아니고 통계적으로 수용할 수 있게 만들어놓았다.
원래의 샘플의 위치를 $x_0$라고 하고 제안 분포를 통해 새로 제안 받은 샘플의 위치를 $x_1$이라고 하자.
이 때, target 분포를 지금까지 처럼 $f(x)$라고 하면 다음에 대해 확인해본다.
uniform distribution $U_{(0,1)}$에서 부터 추출한 임의의 샘플 $u$에 대해서,
\[\frac{f(x_1)}{f(x_0)}>u\]만약 수식 (3)이 만족되면, 이 샘플은 비록 타겟 분포에서 새로운 샘플에 대한 높이가 더 높지는 않았지만 수용하게 된다.
만약 여기서도 수식 (3)을 만족하지 못하면 그 때는 새로운 샘플 $x_1$을 샘플링하기를 수용하지 않고, $x_1$을 $x_0$으로 설정한 뒤 다음 샘플($x_2$)을 추천 받는다.
이와 같은 2~3의 단계를 계속 수행해나가면 된다.
알고리즘의 pseudo-code
여기까지가 MCMC 알고리즘의 끝이다. 정말 간단하다.
이 내용을 pseudo-code로 작성하면 다음과 같다.
Initialize $x_0$
For $i=0$ to $N-1$
Sample $u\sim U_{[0,1])}$
Sample $x_{new}~g(x_{new}|x_i))$
If $u\lt A(x_i, x_{new}) = min\left\lbrace 1, f(x_{new})/f(x_i)\right\rbrace$
$\quad x_{i+1} = x_{new}$
else
$\quad x_{i+1} = x_i$
제안 분포가 symmetric 하지 않은 경우는?
위의 샘플링 과정 전체를 통틀어 제안 분포가 symmetric 하지 않은 경우에 관한 알고리즘이 Metropolis 알고리즘을 업그레이드한 Metropolis-Hastings 알고리즘이다.
Metropolis-Hastings 알고리즘에서는 수식 (2)에서 보였던 타겟 분포의 likelihood 비교 시에 제안 분포의 높이도 함께 이용해 그 값을 보정해주어야 한다.
즉, 수식 (2)의 기준은 다음과 같이 보정될 수 있다.
제안 분포를 $g(x)$라고 할 때,
\[수식(2) \Rightarrow \frac{f(x_1)/g(x_1|x_0)} {f(x_0)/g(x_0|x_1)}\]다시 말해 수식 (4)의 분자를 보면 새로운 포인트 $x_1$에 대해서는 $x_0$를 기준으로 뽑은 $g(x_1|x_0)$ 값을 이용해 정규화 해주고,
또, 이전의 포인트 $x_0$에 대해서는 새로운 $x_1$을 기준으로 $g(x_0|x_1)$의 값을 이용해 정규화 해주었다고 볼 수 있다.
샘플링 결과
위에서 설명한 Metropolis 알고리즘을 이용해 샘플링을 하면 아래와 같은 결과를 얻을 수 있다.
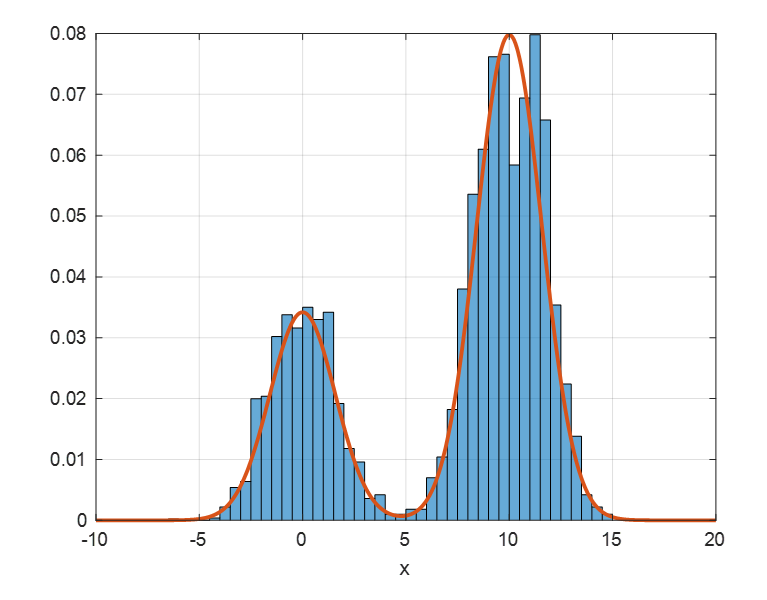
그림 5. MCMC 알고리즘을 이용해 샘플링한 결과
이 결과를 얻기 위한 MATLAB 코드는 아래와 같다.
clear; close all; clc;
% 참고문헌: https://www.cs.ubc.ca/~arnaud/andrieu_defreitas_doucet_jordan_intromontecarlomachinelearning.pdf
%
%
rng(1)
n_iter = 5000;
target = @(x) 0.3*exp(-0.2 * x.^2) + 0.7 * exp(-0.2 * (x - 10).^2);
xx = linspace(-10,20, 1000);
%% Metropolis Hastings
% initialize x_0
x = [];
x = [x, (rand(1, 1) - 0.5) * 30 + 5]; % -10에서 20사이의 범위에서 random uniform
proposal = @(x, mu, s) 1/(s*sqrt(2*pi))*exp(-(x-mu)^2/(2*s^2)); % 정규분포
my_std = 10;
for i = 1 : n_iter
u = rand(1); % sample u
x_old = x(i);
% 제안 분포 q(x_new | x_old) = N(x_old, sigma)로부터 샘플 추출
x_new = randn(1) * my_std + x_old;
% A(x_old, x_new) 계산
A = min(1, ...
(target(x_new) * proposal(x_old, x_new, my_std)) / ...
(target(x_old) * proposal(x_new, x_old, my_std))...
);
if u < A
x = [x x_new];
else
x = [x x_old];
end
end
%% 결과 plot
figure; h = histogram(x,'BinWidth',0.5, 'Normalization','probability');
hold on; plot(xx, target(xx)/max(target(xx))*max(h.Values),'linewidth',2)
grid on;
xlabel('x');
MCMC를 이용한 Bayesian estimation
샘플링 뿐만 아니라 MCMC는 파라미터 추정에도 사용될 수 있다.
prerequisites
이 내용에 대해 잘 이해하시려면 다음의 내용에 대해 알고 오시는 것을 추천드립니다.
주어진 것은 무엇인가?
이번에는 MCMC를 이용해 파라미터 추정을 수행해보도록 하자.
가령, 다음과 같이 평균이 10, 표준편차가 3인 정규분포를 따르는 30,000 개의 원소들로 구성된 모집단에서 1,000개의 표본을 추출할 수 있었다고 해보자.
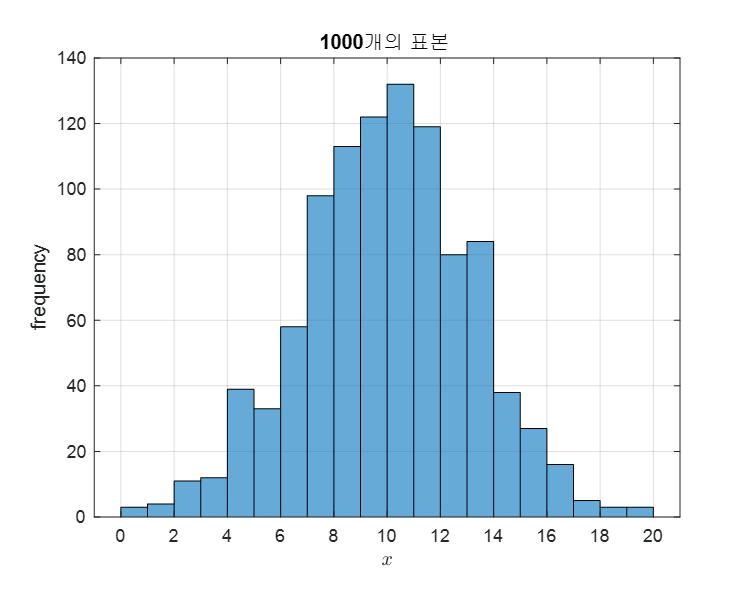
그림 6. Bayesian estimation을 위해 준비된 1,000개의 샘플
우리가 알고싶은 것은 이 1,000개의 샘플만을 이용해서 30,000개의 전체 모집단의 평균 값을 더 잘 추정해보는 것이다.
추정 과정
1. random initialization
기본적으로 MCMC의 샘플링 과정과 동일하게 파라미터 추정 시에도 random initialization으로 MCMC 알고리즘이 시작된다.
우리가 추정하고자 하는 모집단의 확률밀도함수는 정규분포를 따른다고 알고있다고 하면, 우리는 평균과 표준편차 두 가지 파라미터에 대해 추정해볼 수 있겠다.
하지만, 여기서는 설명의 편의를 위해 평균 값에 대해서만 추정하고 표준편차는 표본 표준편차를 그대로 사용하도록 하자.
먼저, random하게 initialize하는 것이 원칙이나 평균값 1로부터 시작해서 실제로 추정값이 참값인 10에 가까워지는지 확인해보자.
위 1,000개의 샘플의 표본 표준편차는 3.1591이라고 계산할 수 있었다.
따라서 우리의 타겟분포는 가우시안 분포이며, 그 표준편차는 3.1591로 계속 고정된 채로 움직일 것이다.
2. 제안 분포를 이용해 mean 값을 제안 받기
샘플링 과정과 동일한 방식으로 MCMC에서 이용되는 알고리즘을 이용해 제안 분포를 통해 새로운 mean 값을 추천 받도록 하자.
그러기 위해 initialize 된 평균값 1을 중심으로 제안 분포를 하나 그리자.
제안 분포는 어떤 것을 사용하여도 좋지만 논의의 편의성을 위해 symmetric한 확률분포 중 하나인 정규분포를 이용하자.
제안 분포로 사용되는 정규분포는 표준편차가 0.5인 것을 이용할 것이다.
그러면 이 제안분포에서 샘플링을 통해 새로운 mean 값을 추천받을 수 있다.
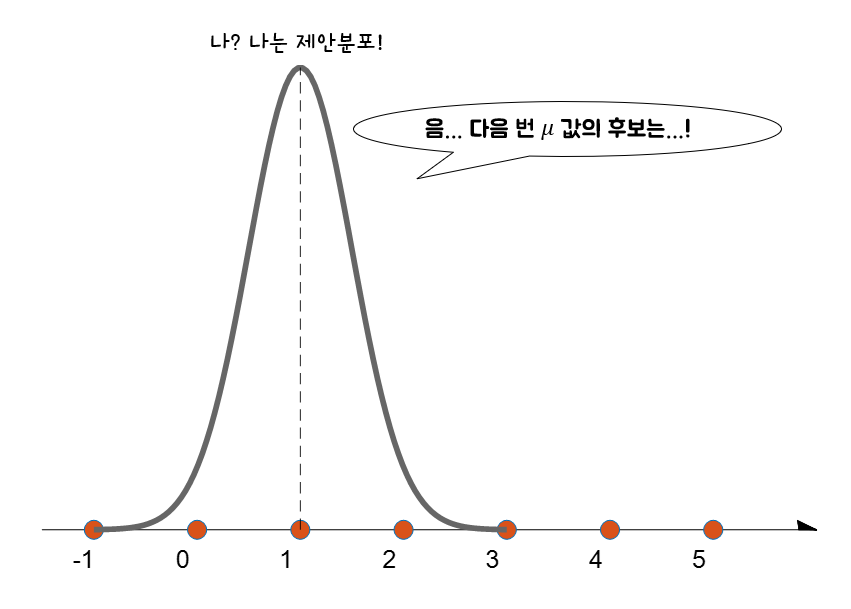
그림 7. $\mu=\mu_{old}$가 중심인 제안 분포로부터 새로운 샘플을 추출해 새로운 $\mu$를 추천받을 수 있다.
3. 추천 받은 제안에 대한 수락 혹은 거절
※ 여기서부터는 베이즈 정리가 나오고 수식이 복잡해지만, 마지막 식 (13)의 결과만 알고있어도 MCMC를 이해하는데에는 큰 무리가 없음. ※
그럼 이제는 추천 받은 mean 값을 accept하거나 reject해야한다.
accept 혹은 reject의 기준은 이전의 sampling method에서와 마찬가지로 타겟 함수의 높이 비교를 통해 이루어질 수 있다.
하지만, 약간 다른 것은 이번에는 타겟 함수의 파라미터가 변경된 두 경우를 비교하는 것이라는 점이다. 왜 파라미터가 변경된 두 경우에 대한 비교를 수행하는 것일까? 그것은 지금하고자 하는 일이 파라미터 추정이며 파라미터 추정에서는 이전 파라미터(여기서는 평균)에 비해 지금 파라미터가 더 좋은가를 확인해야하기 때문이다.
다시 말해, 아래와 같은 수식을 기준으로 비교가 이루어진다고 할 수 있다. 이 비교 기준을 만족하면 제안을 수락하고 그렇지 못하면 거절하게 된다.
\[기준: \frac{f_{new}(x)}{f_{old}(x)} > 1\]식 (5)를 다시 쓰면 다음과 같이도 쓸 수 있다.
\[\frac{P(\theta = \theta_{new}|Data)}{P(\theta = \theta_{old}|Data)}>1\]식 (6)에서 $Data$는 그림 6에서 본 1,000개의 샘플이라고 할 수 있다.
여기서, 베이즈 정리에 따라 식 (6)을 변형시키면 다음과 같다.
\[\frac{f(D|\theta=\theta_{new})P(\theta=\theta_{new})/f(D)} {f(D|\theta=\theta_{old})P(\theta=\theta_{old})/f(D)}>1\]식 (7)에서 $f(D)$는 분자 분모에서 동일하므로 제거하면 아래와 같다.
\[식(7) \Rightarrow \frac{f(D|\theta=\theta_{new})P(\theta=\theta_{new})} {f(D|\theta=\theta_{old})P(\theta=\theta_{old})}>1\]분자나 분모에서 $f(D|\theta)$와 관련된 항은 모두 전체 데이터의 likelihood를 의미하는데 모든 데이터가 독립적으로 얻어졌다고 가정하면 다음과 같이 각각의 데이터에 대해 풀어쓸 수 있게 된다.
\[f(D|\theta) = \prod_{i=1}^N f(d_i|\theta)\]여기서 전체 데이터의 개수가 $N$개이고 각각의 데이터들은 $d_i$로 표현했다.
여기서 우리의 target 분포는 정규분포이므로,
\[식(9)\Rightarrow \prod_{i=1}^{N}\frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(d_i-\mu)^2}{2\sigma^2}\right)\]계산의 편의를 위해 식 (10)에 자연로그를 취하도록 하자.
\[\Rightarrow \sum_{i=1}^{N}\left\lbrace\log\left(\frac{1}{\sigma\sqrt{2\pi}}\right)-\frac{(d_i-\mu)^2}{2\sigma^2}\right\rbrace\] \[=\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu)^2}{2\sigma^2}\right\rbrace\]이제 원래의 식 (8)도 마찬가지로 자연로그를 취해주고, 식 (12)를 대입해주면 아래와 같다.
\[식(8)\Rightarrow \frac{\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{new})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{new}))} {\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{old})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{old}))} > 1\]그럼 식 (13)이 의미하는 바는 무엇일까?
이것은 주어진 데이터에 대해 $\mu=\mu_{old}$인 경우와 $\mu=\mu_{new}$인 경우의 likelihood $\times$ prior를 비교한 것과 같다는 것을 알 수 있다.
아래의 그림 8에서는 기존의 $\mu = \mu_{old}$인 경우와 $\mu=\mu_{new}$인 경우의 target 분포에 대해 모든 데이터로부터 likelihood 값을 얻는 과정을 보여주고 있다.
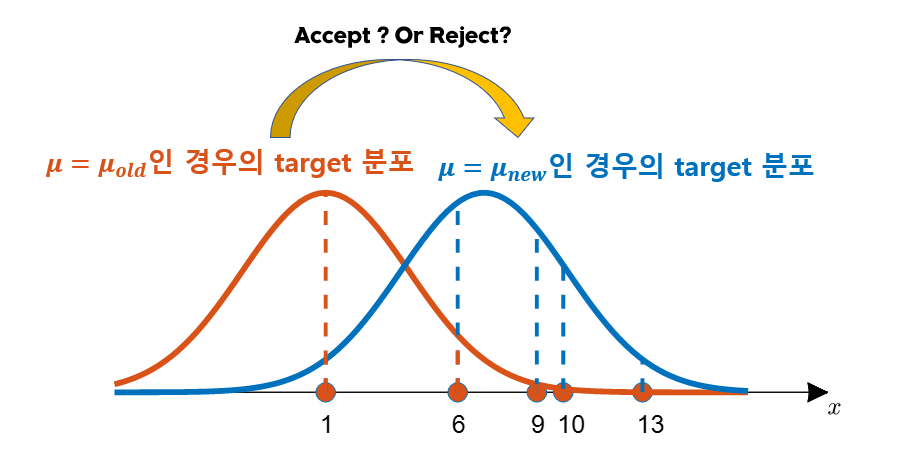
그림 8. $\mu=\mu_{old}$인 경우와 $\mu=\mu_{new}$ 인 경우에 대해 모든 데이터의 likelihood들을 곱해주는 과정
비록 그림 8에서는 5개의 데이터만 보여주었지만, $\mu=\mu_{old}$인 경우에 비해 $\mu=\mu_{new}$인 경우가 실제 모평균 값(10)과 더 가깝기 때문에 더 likelihood(확률밀도함수의 높이)가 큰 데이터들이 많고 실제로 likelihood를 모두 곱해준 뒤 prior와 곱해 비교해주면 $\mu=\mu_{new}$로 추천한 것이 채택될 수 있을 것이다.
이제, 식 (13)을 보면 $\sigma$와 $\mu_{new}$, $\mu_{old}$는 모두 주어져 있기 때문에 계산을 하는데 아무런 문제가 없지만 $P(\mu=\mu_{new})$나 $P(\mu=\mu_{old})$와 같은 prior는 어떻게 계산 해주어야 할까?
베이즈 정리의 의미편이나 Naive Bayes 분류기 편에서 보았던 것 처럼 Prior는 일종의 사전지식으로, 여기서는 굉장히 사소하더라도 $\mu$ 값에 대한 정보를 입력해주면 된다.
여기서는 그림 6을 봤을 때 대략적으로나마 알 수 있는 것 처럼 추정하고자 하는 $\mu$값은 최소한 0보다는 클것이라는 사전 지식을 이용해주자. 즉, 여기서는 prior를 아래와 같이 설정할 수 있다.
\[P(\mu) = \begin{cases}1 && \text{if }\mu\gt 0 \\ 0 && \text{otherwise}\end{cases}\]만약 더 확신이 있다면 0보다 크다는 조건 보다는 더 좋은 조건을 사용할 수도 있을 것이다. (가령 3보다는 크다 같은…)
어찌되었든 우리는 식 (13)을 만족할 때 새로 추천 받은 $\mu_{new}$를 수용할 것이고 그렇지 못한 경우는 reject 할 것이다.
하지만, MCMC를 이용한 Bayesian Estimation에서도 Sampling method 때와 마찬가지로 패자부활전을 거칠 수 있다.
4. 패자부활전
만약 식 (13)을 만족하지 못한 경우에는 샘플링 method때와 마찬가지로 패자부활전을 거칠 수 있다.
이 때, $[0,1]$의 interval을 가지는 uniform distribution $U_{[0, 1]}$으로부터 추출한 $u$에 대해서 다음을 만족할 경우 $\mu_{new}$로 수용할 수 있다.
\[\frac{\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{new})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{new}))} {\sum_{i=1}^{N}\left\lbrace-\log(\sigma\sqrt{2\pi})-\frac{(d_i-\mu_{old})^2}{2\sigma^2}\right\rbrace + \log(P(\mu = \mu_{old}))} > u \notag\] \[\text{where } u \sim U_{[0, 1]}\]추정의 결과
그림 9를 보면 처음에 $\mu$ 값을 1부터 시작해 서서히 추정해나가면서 모평균인 10에 가까워져 가는 것을 알 수 있다. 약 20 iteration 이후부터 실제 모평균에 가까운 값에서 진동하는 것을 볼 수 있기도 하다.
우리는 보통 이렇게 초기의 iteration 동안 실제 모평균에 수렴하기 위해 거치는 단계를 burn-in period라고 부른다.
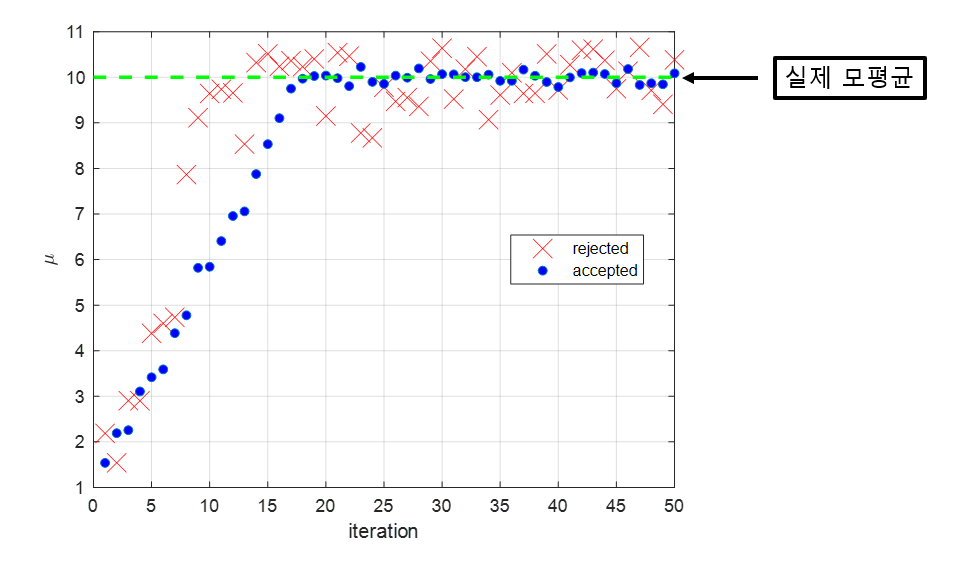
그림 9. 처음 50 iteration 동안의 수용되거나 거절된 $\mu$ 값들
그림 10에서는 12,000 iteration 동안 수용되거나 거절된 $\mu$값을 표현하였다.
그림 10을 보면 모평균인 10에서 멀어진 경우가 추천되면 거절되지만 모평균인 10에 가까운 경우가 추천되면 수용된 것을 볼 수 있다.
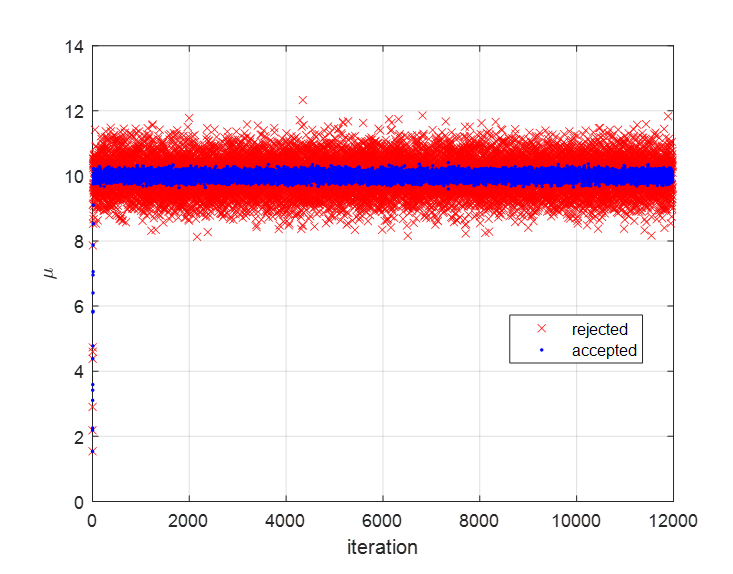
그림 10. 전체 12,000 iteration 동안의 수용되거나 거절된 $\mu$ 값들
처음의 25% iteration 구간을 burn-in period로 잡고 나머지 75%의 iteration 동안 수용된 $\mu$값을 모두 평균 해 보면 그 값이 9.99 임을 알 수 있었고, 이는 모평균인 10에 매우 가까운 것임을 알 수 있었다.
이렇게 구한 모평균인 9.99를 이용해 모집단의 분포를 추정하면 아래의 그림 11과 같이 원래의 모집단과 매우 유사한 분포를 가진다는 것을 알 수 있을 것이다.
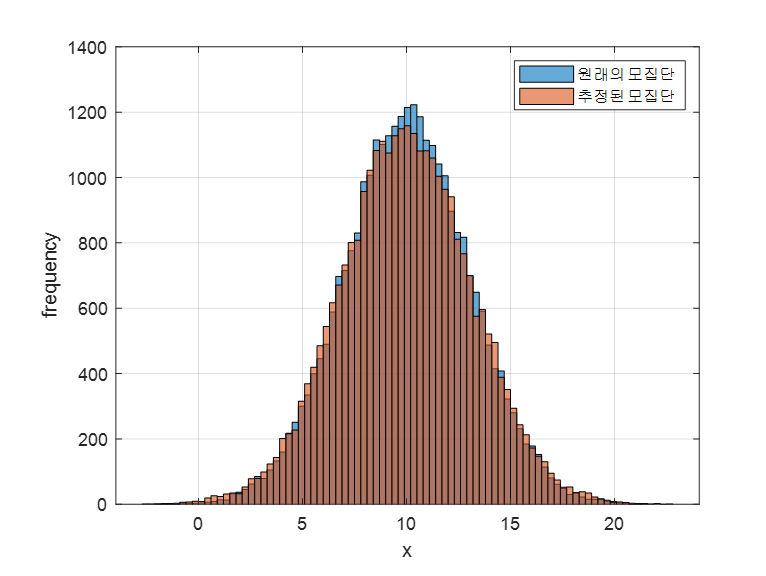
그림 11. 원래의 모집단의 분포와 추정된 $\mu$ 값을 이용해 추정한 모집단의 분포
※ MCMC를 이용한 Bayesian Estimation의 MATLAB 코드는 아래의 위치에서 받아가실 수 있습니다.
https://github.com/angeloyeo/gongdols/tree/master/%ED%86%B5%EA%B3%84%ED%95%99/MCMC/metropolis_hastings/Bayesian_estimation_with_MCMC
참고자료
- An introduction to MCMC for Maching Learning / C. Andrieu et al., Machine Learning, 50, 5-43, 2003
- 서울대학교 통계학과 김용대 교수님의 강의노트
- From Scratch: Bayesian Inference, Markov Chain Monte Carlo and Metropolis Hastings, in Python, Joseph Moukarzel