지금껏 우리는 정현파 기초, 복소수 기초, Phasor에 대해 다루면서 ‘신호의 표현’에 대해 다루었다고 할 수 있다.

지금부터는 가장 기초적인 시스템 특성인 선형성과 시불변성에 대해 알아보고자 한다. 이 두 특성을 동시에 가지는 시스템을 선형 시불변(Linear Time-Invariant) 시스템이라고 부른다.

Prerequisites

이 포스팅을 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.

• 신호 처리 서론
• 정현파 기초
• Phasor

아래의 내용은 알고 계시면 좋지만 꼭 몰라도 전체 내용에는 지장 없을 선행 지식입니다.

• 벡터의 기본 연산(상수배, 덧셈)
• 행렬과 선형 변환

어떤 신호라도 정현파의 조합으로 표현할 수 있다.

신호 시스템을 공부함에 있어 가장 핵심 포인트를 하나 꼽으라면 “어떤 신호라도 정현파의 조합으로 표현할 수 있다”는 말이다.

우리는 이 말에 대해서 점점 더 공부해가게 될 것이다. 당장은 이해하기 어려울 수 있지만, 예시를 확인해가면서 조금씩 익숙해져보자.

참고로 이 말을 수학적으로 증명하는 것은 매우 어렵기 때문에 깊이 이해하려 하기 보다는 받아들이는 편이 낫다.

아래의 그림을 보면 사각파를 정현파의 조합으로 어떻게 표현할 수 있는지를 나타내었다.

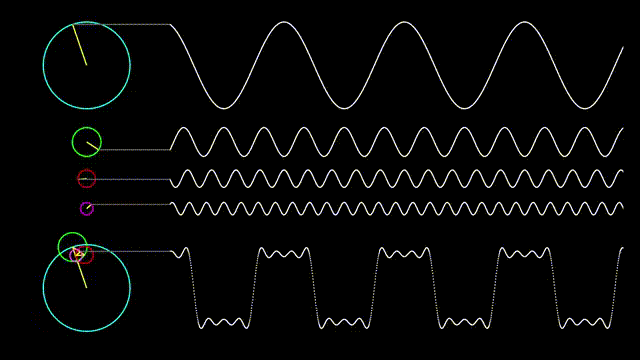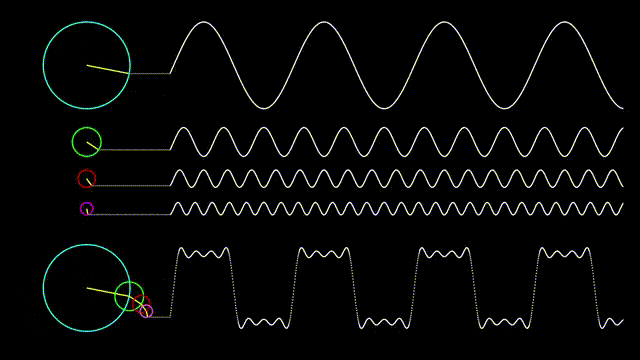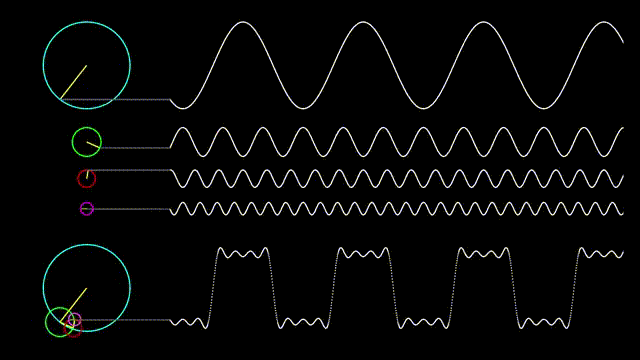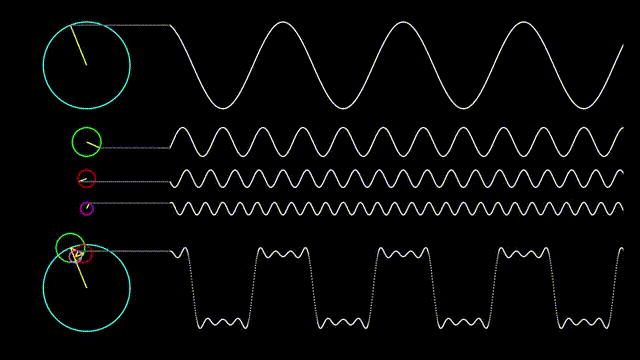
그림 1. 사각파를 정현파로 분해하여 표현한 그림
출처: Rala Sun Blog

신호의 범주는 단순 사각파에서 그치지 않고 그림마저도 포함된다. 그림도 2차원 평면 상에 그려지는 신호로 볼 수 있기 때문인데, 2차원 평면 상의 신호라도 다양한 주기의 원을 이용해 표현할 수 있다.

그림 2. 어떤 신호라도 정현파의 조합으로 구성해낼 수 있다.
출처: @gfycat by spolanski

그럼, 어떤 주파수를 가지는 정현파들을 얼마나 조합할것인가? 라는 질문이 생길 수도 있지만, 이것에 관해서는 “푸리에 시리즈”나 “푸리에 변환” 편에서 더 자세하게 알아보고,

지금 말하고자 하는 핵심 포인트는 “어떤 신호라도 정현파의 조합으로 표현할 수 있다”는 점이다¹.

이제 임의의 신호를 아래의 그림처럼 쪼개서 생각해보자.

신호는 시간에 따른 변화 뿐만 아니라 주파수 성분별로도 구별할 수 있다고 보자는 것이다.

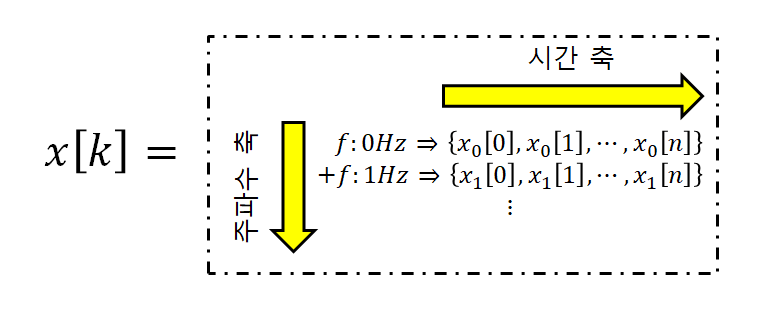
그림 3. 임의의 신호를 주파수 성분별로 생각하면, 시간 축, 주파수 축의 여러 요소로 분해해 볼 수 있다.

어떻게 생각하면 가로 줄 한 줄짜리로 생각했던 신호가 사실은 하나의 테이블로 구성되는 것이라고 생각할 수도 있는 것이다. 그리고, 가로, 세로 축은 시간과 주파수 축을 의미한다고 볼 수 있는 것이다.

신호 처리 서론에서는 시스템(system)이란 입력 신호를 받고 출력 신호를 내보내는 함수와 유사한 것이라고 한 바 있다.

그리고, 출력 신호는 입력 신호를 특정한 “규칙”으로 변형해 내보내게 된다.

만약 신호가 주파수, 시간의 두 축을 가지는 테이블로 표현되는 것이라고 한다면, 이 “규칙”이 어떤 시간, 어떤 주파수 성분에 대해 동일하게 적용되지 않는다면 연산이 굉장히 복잡해질 것임은 뻔하다.

다시 말해, 단순한 시스템은 시간의 변화에 따라 불변하는 것이어야 한다.

또, 각 주파수 성분별로 쪼개서 동일한 “규칙”을 적용해볼 수 있어야 단순한 시스템이다. 즉, 각 주파수 성분별로 “규칙”을 적용해 합치는 것이 이미 합쳐진 신호에 “규칙”을 적용한 것과 차이가 없어야 한다.

단순한 것이 최고다. 글도 어렵게 쓰는 것보다 쉽게 쓸 수 있어야 하고, 어렵고 복잡한 설명보다는 단순하게 설명하는 것이 더 프로페셔널 한 것이라고 생각한다.

그런 의미에서 시스템도 단순한 것 부터 공부하기 시작한다. 이렇게 “단순한” 시스템을 선형-시불변 시스템(Linear Time-Invariant system)이라고 부른다.

선형-시불변 시스템(Linear Time Invariant System)

시불변성

시간이 바뀌면서 시스템이 바뀌어 버리면 시스템이 복잡해진다. 매 시간 포인트마다 다른 시스템을 생각해야 하는 것이니 말이다.

시불변성은 다음과 같이 표현할 수 있다. 입력이 $n_0$만큼 지연되었을 대 출력도 같은 정도로 지연된다면 시불변 시스템이라고 할 수 있다.

\[x[n-n_0] \longmapsto y[n-n_0]\]

시스템의 시불변성을 체크해보기 위해서는 입력 신호에 delay를 먼저 걸고 system을 통과시켜 본 결과와 입력 신호를 시스템에 통과 시킨 후 delay를 걸어줘서 얻은 결과를 비교해보면 된다.

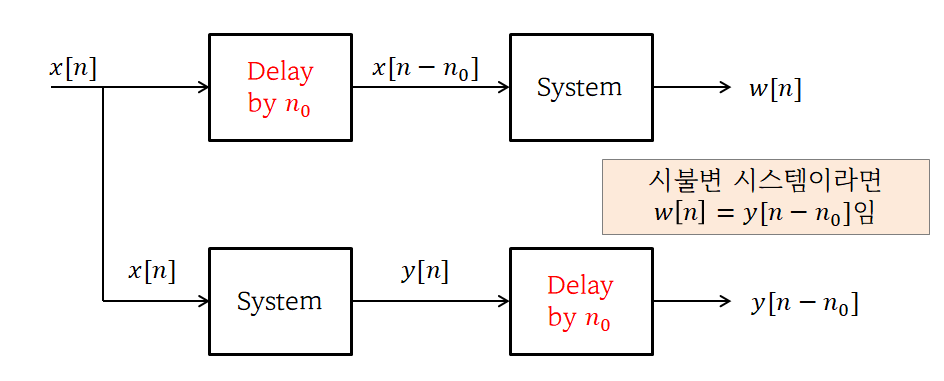
그림 4. 시불변 특성을 검사하기 위해 수행할 수 있는 테스트의 모식도

가령, 아래와 같은 시스템을 생각해보자.

\[y[n]=(x[n])^2\]

이 시스템이 시불변 시스템인지 보기 위해서 다음 두 가지를 확인해보자.

\[w[n]=(x[n-n_0])^2\] \[y[n-n_0]=(x[n-n_0])^2\]

여기서 $w[n]=y[n-n_0]$ 이므로 이 시스템은 시불변 시스템이다.

반면에 아래와 같은 시스템을 생각해보자.

\[y[n]=x[-n]\]

이 시스템이 시불변 시스템인지 확인하기 위해 다음 두 가지를 확인해보자.

\[w[n]=x[(-n)-n_0]\] \[y[n-n_0]=x[-(n-n_0)]\]

여기서 $w[n]\neq y[n-n_0]$이므로 이 시스템은 시불변 시스템이 아니다.

선형성

앞서 설명했던 바와 같이 신호 내 성분별로 시스템이 다르게 적용되어야 하면 시스템이 복잡해진다. 따라서, 선형성을 만족하는 시스템을 이용하면 시스템을 적용시키는 연산을 단순화시킬 수 있다.

선형성은 다음과 같이 정의된다. $x_1[n]\longmapsto y_1[n]$이고 $x_2[n] \longmapsto y_2[n]$이라고 했을 때 다음이 성립하면 선형적이다.

\[x[n]=\alpha x_1[n]+\beta x_2[n] \longmapsto y[n]=\alpha y_1[n]+\beta y_2[n]\]

선형성이 성립하는 시스템에서는 신호 내에 있는 신호 성분별로 시스템을 각각 적용해 상수배해주어 합해주는 것이 가능해진다. (어렵게 말하면 중첩의 원리라고도 부른다.)

그렇기 때문에 모든 주파수에 대해 한번에 다루지 않고 각 주파수 별로 다루는 방법에 대해 충분히 익혀야 한다. (Phasor는 하나의 주파수에 대한 처리를 취급하는 방법이다.)

또, 위 식을 잘 생각해보면 $\alpha,\beta = 1$인 경우에는

\[x[n]=x_1[n]+x_2[n] \longmapsto y[n]=y_1[n]+y_2[n]\]

이고, 상수 하나만 이용하면,

\[x[n]=\alpha x_1[n] \longmapsto y[n]=\alpha y_1[n]\]

이다. 이것은 벡터의 기본 연산(상수배, 덧셈)을 써놓은 것과 같다는 것을 알 수 있다.

따라서, 선형성이 성립한다는 말은 신호를 벡터로 볼 수 있다는 말과도 같다.

또, 선형성이 성립하는 시스템은 선형 변환으로 볼 수 있다.

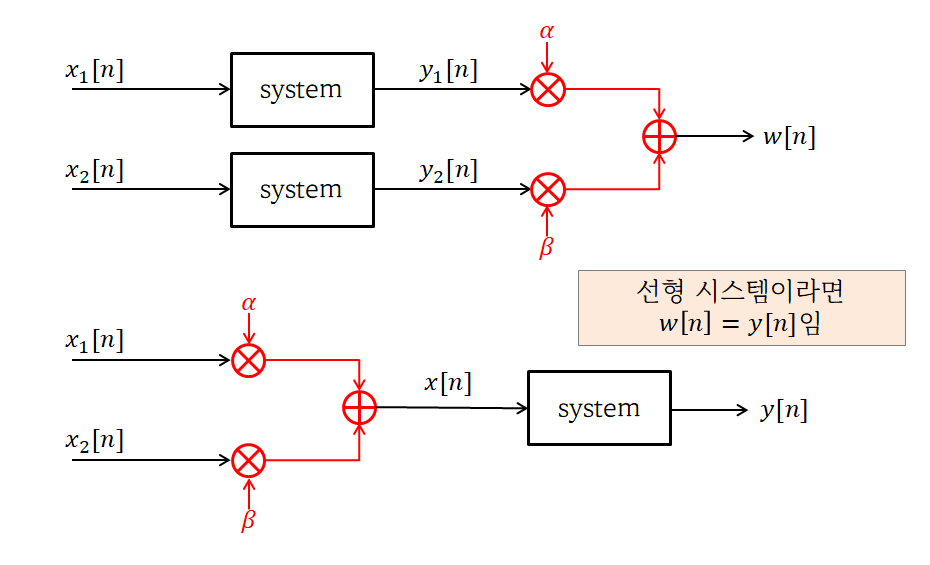
그림 5. 선형성을 검사하기 위해 수행할 수 있는 테스트의 모식도

선형시스템 판별에 대해 예를 들어 $y[n]=(x[n])^2$과 같은 시스템을 생각해보자.

이 시스템이 선형적인지 판별하기 위해 아래의 두 함수를 생각해보면,

\[w[n]=\alpha(x_1[n])^2 + \beta (x_2[n])^2\] \[y[n]=(\alpha x_1[n])+\beta (x_2[n])^2 = \alpha^2 (x_1[n])^2 + 2\alpha\beta x_1[n]x_2[n]+\beta ^2 (x_2[n])^2\]

이 두 함수가 다르다는 것을 알 수 있으므로, 제곱 시스템은 비선형 시스템이다.

LTI 체계의 유용성

결국 Linear 시스템을 이용하면 신호를 벡터처럼 다룰 수 있고, 시스템을 선형 변환처럼 다룰 수 있게 된다.

그리고, Time-Invariant 시스템을 이용하면 모든 시간 point에 대해 동일한 시스템을 이용해 변환을 적용할 수 있게 되니 계산이 전체적으로 편리해진다.

이 말은 선형대수학에서 사용되는 개념들을 신호/시스템 분야에 확장할 수 있다는 의미가 된다. 이러한 개념은 벡터 공간의 개념을 신호 공간(signal space)으로 확장할 수 있게 만드는 기초가 된다.