파라미터 p를 수정해가며 다양한 경우의 기하 분포의 생김새에 대해 확인해보자.
기하 분포에서 x 축에 있는 k가 갖는 것은 어떤 의미일까?
그리고 기하 분포의 형태가 의미하는 것을 설명할 수 있는가?
Prerequisites
기하 분포를 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
기하 분포의 정의
기하 분포는 성공 혹은 실패의 두 가지 경우의 수로 구성된 시행을 연달아 수행 시 처음 성공할 때 까지 시도한 횟수 $k$에 대한 분포이다.
성공 확률이 $p$인 시행에 대해 $k$번 시행 후 첫번째 성공을 얻을 확률은
\[P(K=k) = (1-p)^{k-1}p\]여기서 $k = 1, 2, 3, \cdots $이다.
여기서 잘 보면 확률값 $P(K=k)$의 수열은 $(1-p)$를 매 항마다 계속해서 곱해나가는 수열이므로 등비 수열이 되는데,
등비 수열의 또 다른 이름이 기하 수열(geometric sequence)이다보니 이 분포는 기하 분포라는 이름을 얻었다.
기하 분포의 형태
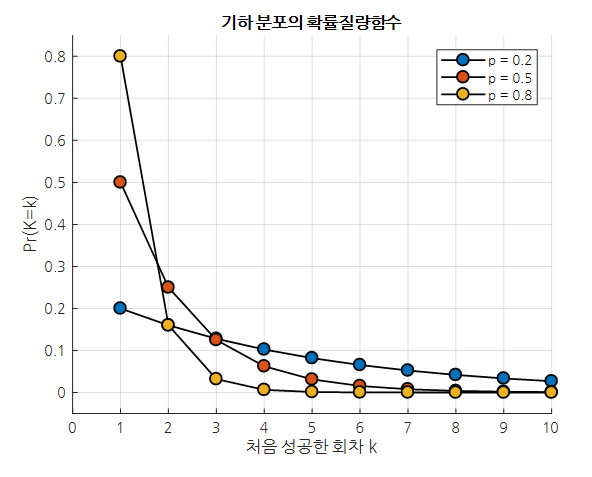
그림 1. 다양한 p 값에 대한 기하 분포의 형태
기하 분포에서 보여주는 것은 성공 확률이 $p$일 때 $k$ 번째 처음으로 성공할 수 있는 확률을 의미한다.
예를 들어 그림 1에서 p = 0.8인 경우에 대해 첫 번째 시도에서 성공할 확률은 0.8이고, 두 번째 시도에서 성공할 확률은 한번 실패한 뒤 성공해야 하므로 0.2 * 0.8 = 0.16이다.
또, 세 번째 시도에서 성공할 확률은 0.2 * 0.2 * 0.8 = 0.032와 같다.
여기서 알 수 있는 것은 $p$ 값이 클 수록 $k=1$에서의 성공확률값도 당연히 크다는 것이다.
한가지 위로가 되는 점은 $p$ 값이 크지 않은 경우 여러번 시도했을 때 $p$값이 큰 경우보다 더 높은 확률로 첫 성공을 달성할 수 있다는 것이다.
기하 분포 문제 풀이
기하 분포는 생각 보다 문제가 와닿는 것들이 많고, 식 자체가 복잡하지 않다보니 문제 풀기에 어렵지는 않을 것 같다.
문제 1.
주사위가 1이 나올 때 까지 계속해서 던져보고 있다고 하자. 주사위가 6번째가 되어서야 1이 나올 확률을 계산하시오.
문제 1 Solution
주사위가 1이 나올 확률은 1/6이므로, 6번째에서 1이 나올 확률은 5번 동안 1이 나오지 않고, 6번째에서 1이 나오는 것과 동일하다.
따라서,
\[\Rightarrow (5/6)^5\times (1/6)^1=0.06698\]약 6.7%이다.
문제 2.
통과율이 극악이라 알려진 시험이 있다. 이 시험의 통과율은 20%라고 한다. 어떤 사람이 세 번 내에 이 시험을 통과할 확률은?
문제 2 Solution
이 문제에서는 1번에 합격할 확률 + 2번째에 합격할 확률 + 3번째에 합격할 확률을 모두 더해서 계산하면 된다.
따라서,
\[\Rightarrow (0.2) + (0.8)\times(0.2) + (0.8)^2\times(0.2) = 0.448\]즉, 44.8%의 확률로 세번 안에 합격할 수 있다.