행렬식의 성질
크래머 공식을 잘 이해하기 위해선 아래의 몇 가지 행렬식의 성질을 잘 이해하고 하면 좋다.
- 행렬식은 각 열벡터로 구성된 평행사변형의 넓이와 같은 의미를 갖는다.
가령 임의의 행렬
\[A=\begin{bmatrix}a & b \\ c & d\end{bmatrix}\]에 대해 각 열들을 $U$, $V$라고 한다면 $\det(A)=ad-bc$는 아래의 평행사변형의 넓이와 같다.
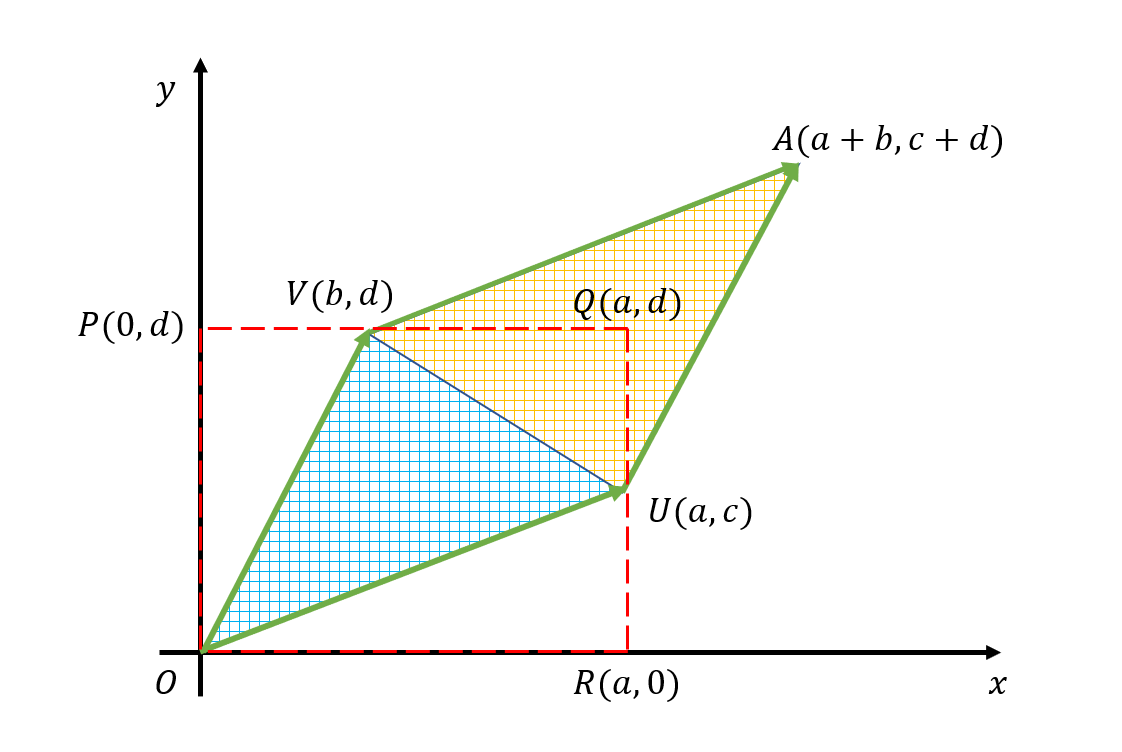
그림 1. 행렬식의 값은 $U$, $V$ 벡터로 구성된 평행사변형의 넓이와 같다.
따라서, 평행사변형을 구성하는 벡터가 평행이라면 이 평행사변형의 넓이는 무조건 0이 된다.
다른 말로는 행렬 $A$의 열벡터가 모두 선형독립이 아니라면 평행사변형의 넓이는 0이 되고 역행렬을 가지지 않는 행렬이 된다.
- 행렬 $A$의 하나의 열이 $k$배 되면 행렬식의 값도 $k$배 된다.
다시 말해 행렬식은 아래와 같은 성질을 만족한다.
\[\det\left(\begin{bmatrix}a & k\cdot b \\c & k\cdot d\end{bmatrix}\right)=k\cdot\det\left(\begin{bmatrix}a & b \\ c & d\end{bmatrix}\right)\]이것은 그림 1에서 평행사변형의 변 중 하나가 $k$배 된 경우를 상상해보면 이해하기 쉽다.
- $A_1, A_2, B_1, B_2, A_n$ 등이 열벡터이고 $k_1, k_2$는 스칼라라고 하자. 이 때, $[]$를 이용해 열벡터를 묶은 행렬을 표현할 때, 행렬식은 아래와 같은 결과를 만족한다.
크래머 공식
크래머 공식은 아래와 같은 방정식의 해를 얻을 때 사용할 수 있는 공식이다.
임의의 $n\times n$ 사이즈의 행렬 $A$와 $n\times 1$ 사이즈의 벡터 $b$이고 $x=[x_1, x_2, \cdots, x_n]^T$라고 할 때,
\[Ax=b\]가 성립할 때, 솔루션 $x$의 각 원소 $x_i\text{ for }i=1,2,\cdots, n$는
\[x_i = \frac{\text{det}(A^{rep}_{i})}{\text{det}(A)}\]와 같이 정해진다는 공식이다.
여기서 $A^{rep}_{i}$는 행렬 $A$의 $i$번째 열을 $b$ 벡터로 치환한 행렬이다.
다시 말해 아래와 같은 $Ax=b$라는 식에서,
\[Ax=b \iff \begin{bmatrix} a_{11} & \cdots & \color{red}{a_{1i}} & \cdots & a_{1n}\\ a_{21} & \cdots & \color{red}{a_{2i}} & \cdots & a_{2n}\\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & \color{red}{a_{ni}} & \cdots & a_nn \end{bmatrix} \begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix} = \begin{bmatrix}b_1 \\ b_2 \\ \vdots \\ b_n\end{bmatrix}\]벡터 $x$의 $i$번째 원소 $x_i$는 다음과 같이 정해진다는 것이다.
\[x_i = \frac{\det(A_i^{rep})}{\det(A)}= \frac { \left|\begin{matrix} a_{11} & \cdots & \color{red}{b_{1}} & \cdots & a_{1n}\\ a_{21} & \cdots & \color{red}{b_{2}} & \cdots & a_{2n}\\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & \color{red}{b_{n}} & \cdots & a_nn \end{matrix}\right|} { \left|\begin{matrix} a_{11} & \cdots & a_{1i} & \cdots & a_{1n}\\ a_{21} & \cdots & a_{2i} & \cdots & a_{2n}\\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{ni} & \cdots & a_nn \end{matrix}\right|}\]공식의 증명
행렬 $A$는 아래와 같이 $n$ 개의 열벡터를 양 옆으로 쌓아둔 것과 같다고 할 수 있다.
\[A=\begin{bmatrix} | & | & & | \\ A_1 & A_2 & \cdots & A_n \\ | & | & & | \end{bmatrix}\]그리고, $A$ 행렬의 열 notation을 이용해 $Ax=b$는 다음과 같이도 쓸 수 있다.
$A$의 각 열을
\[\begin{bmatrix} | \\ A_1\\ |\end{bmatrix}, \begin{bmatrix}| \\ A_2\\ |\end{bmatrix}, \cdots, \begin{bmatrix}| \\ A_n\\ |\end{bmatrix}\]이라 하고 $x$의 각 원소를 $x_1$, $x_2$, $\cdots$, $x_n$이라 할 때,
\[Ax=x_1\begin{bmatrix}| \\ A_1\\ |\end{bmatrix}+x_2\begin{bmatrix}| \\ A_2\\ |\end{bmatrix}+\cdots+x_n\begin{bmatrix}| \\ A_n\\ |\end{bmatrix} = b\]과 같이 쓸 수 있는 것이다.
$i$ 번째 열을 $b$ 벡터로 대체한 행렬을 $A^{rep}_{i}$라고 부르자. 다시 말해,
\[A^{rep}_{i} =\begin{bmatrix} | & | & & | & & | \\ A_1 & A_2 & \cdots & b & \cdots & A_n \\ | & | & & | & & | \end{bmatrix}\]와 같은 행렬을 생각하는 것이며 이 때 $b$는 $i$번째 열에 대입된 것이다.
이것을 표기의 편리함을 위해 아래와 같이 줄여서 쓰도록 하자.
\[A^{rep}_{i} = [A_1, A_2, \cdots, b,\cdots,A_n]\]이 표기 역시 $i$번째 열에 $b$벡터가 대입된 것이다.
그럼 여기서 $A^{rep}_{i}$의 행렬식을 계산해보자.
\[\text{det}(A^{rep}_{i}) = \text{det}\left([A_1, A_2, \cdots, b,\cdots,A_n]\right)\]여기서 $b$는 $x_1A_1 + x_2A_2 + \cdots + x_nA_n$과 같으므로,
\[\Rightarrow \text{det}\left([A_1, A_2, \cdots, \color{red}{x_1A_1 + x_2A_2 + \cdots + x_nA_n},\cdots,A_n]\right)\]행렬식의 성질에 의해,
\[\Rightarrow \color{red}{x_1} \text{det}\left([A_1, A_2, \cdots, \color{red}{A_1},\cdots,A_n]\right) \\ \quad + \color{red}{x_2} \text{det}\left([A_1, A_2, \cdots, \color{red}{A_2},\cdots,A_n]\right) \\ \vdots \\ \quad + \color{red}{x_n} \text{det}\left([A_1, A_2, \cdots, \color{red}{A_n},\cdots,A_n]\right)\] \[=\sum_{j=1}^{n}\color{red}{x_j} \text{det}\left([A_1, A_2, \cdots, \color{red}{A_j},\cdots,A_n]\right)\]행렬을 이루는 열벡터 중 선형독립이 아닌 열벡터가 존재하는 경우 행렬식의 값은 0이다.
따라서, 위 식은 $j=i$인 경우에만 0이 아니고 나머지 경우는 모두 0이 된다.
그러므로,
\[\Rightarrow x_i \text{det}\left([A_1, A_2, \cdots, A_i, \cdots, A_n]\right)\]그런데 $[A_1, A_2, \cdots, A_i, \cdots, A_n]$ 행렬은 기존의 $A$ 행렬과 동일하므로 위 식은
\[\Rightarrow x_i \text{det}(A)\]이다.
따라서, 원래의 식과 비교해보면
\[\text{det}(A^{rep}_{i})=x_i\text{det}(A)\]이므로,
\[x_i = \frac{\text{det}(A^{rep}_{i})}{\text{det}(A)}\]임을 알 수 있다.
기하학적 의미
Prerequisites
크래머 공식의 기하학적 의미를 알기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
- 행렬 곱에 대한 또 다른 시각
- 행렬식의 기하학적 의미
- 평행사변형의 넓이 = 밑변 x 높이
기하학적 해석
크래머 공식의 기하학적 의미는 행렬식이 두 벡터가 이루는 평행사변형의 넓이와 같다는 점과 평행사변형의 넓이는 밑변 x 높이로 계산할 수 있다는 사실 두 가지만으로 기하학적 의미를 해석할 수 있다.
아래와 같은 아주 간단한 행렬, 벡터의 곱을 생각해보자.
\[Ax=b\] \[\Rightarrow \begin{bmatrix}a & b \\ c & d\end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix}=\begin{bmatrix}b_1 \\ b_2\end{bmatrix}\]행렬 곱에 대한 또 다른 시각 편에서 열공간을 기반한 해석 파트를 보면 위의 행렬과 벡터의 곱은 다음과 같이도 쓸 수 있는 것이다.
\[x_1\begin{bmatrix}a\\c \end{bmatrix}+x_2\begin{bmatrix}b\\d \end{bmatrix}=\begin{bmatrix}b_1 \\ b_2 \end{bmatrix}\]이것을 그림으로 표현하면 다음과 같다고 할 수 있다.
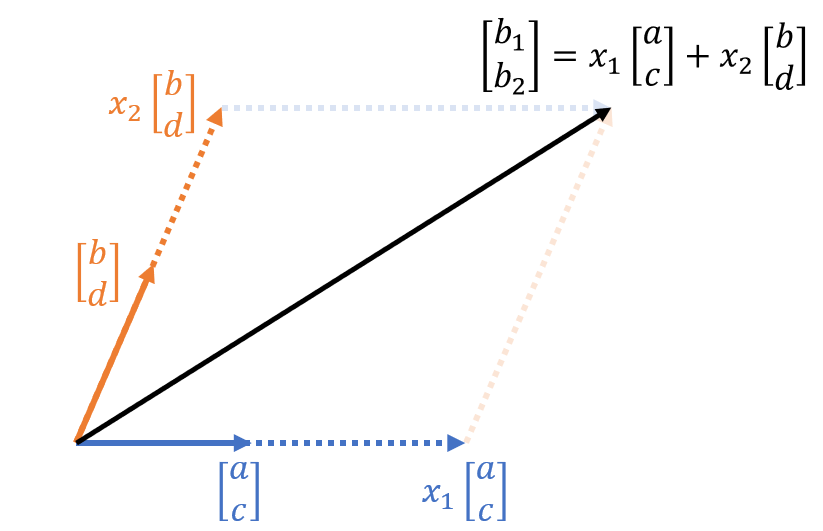
그림 1. 식 (18)의 행렬 벡터 곱을 그림으로 표현한 것
이 때, 우리는 세 개의 평행사변형을 관찰해보도록 하자.
첫 번째는 식 (16)의 행렬 $A$의 각 열 벡터를 두 변으로 하는 평행사변형이다.
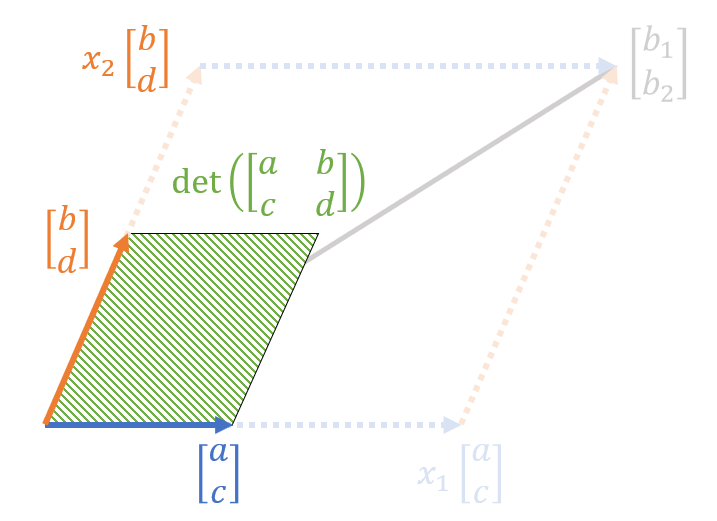
그림 2. 식 (16)의 행렬 $A$의 열벡터로 구성되는 평행사변형
이 평행사변형의 넓이는 행렬식의 기하학적 의미 편에서 보았던 것 처럼 행렬식의 값으로 표현할 수 있다.
두 번째 볼 평행사변형은 아래와 같이 $[b, d]^T$에 $x_2$를 곱한 벡터와 $[a, c]^T$의 두 열벡터로 구성되는 평행사변형이다.
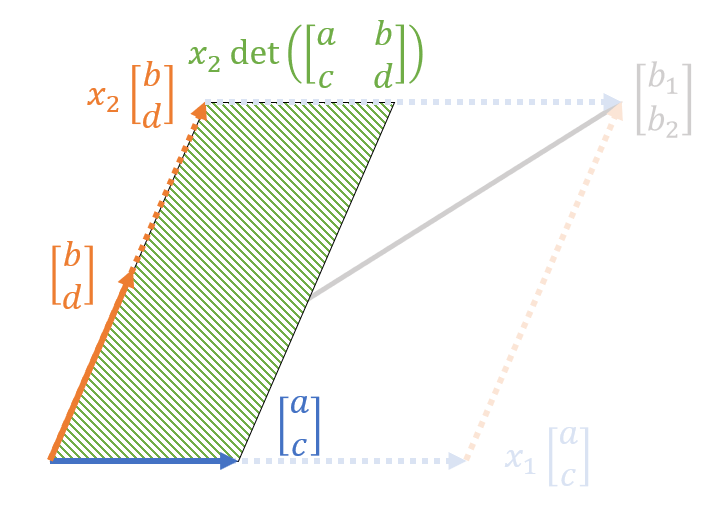
그림 3. $[b, d]^T$에 $x_2$를 곱한 벡터와 $[a, c]^T$의 두 열벡터로 구성되는 평행사변형
이 평행사변형의 넓이를 계산해보면 다음과 같다는 것을 쉽게 알 수 있다.
\[det\left(\begin{bmatrix}a & x_2 b \\ c & x_2 d\end{bmatrix}\right)\]그림 3에서 관찰하는 이 평행사변형은 그림 2에서 보았던 평행사변형의 넓이에서 $x_2$배 만큼 커진 것으로 볼 수 있다.
혹은 위 식에서 행렬식의 특성에 의해 다음과 같이 쓸 수도 있다.
\[\Rightarrow x_2 \ det\left(\begin{bmatrix}a & b \\ c & d\end{bmatrix}\right)\]한편, 세 번째로 관찰해볼 평행사변형은 아래의 그림 4와 같다.
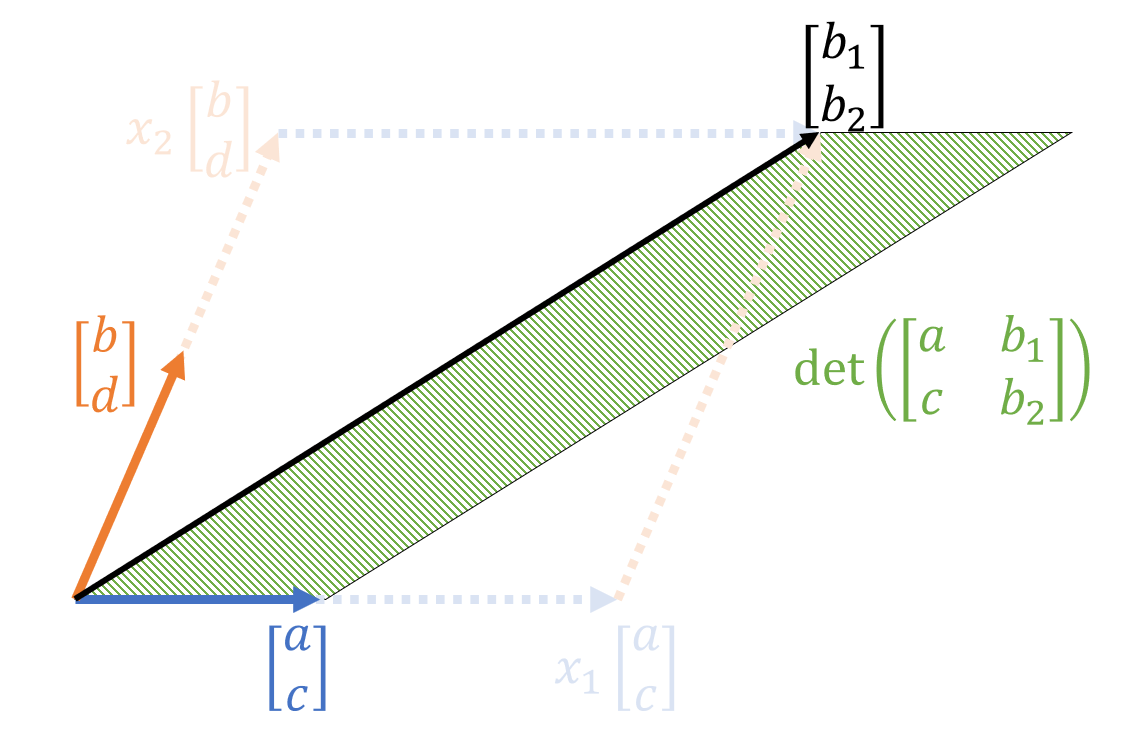
그림 4. $[a,c]^T$ 벡터와 $[b_1, b_2]^T$ 벡터로 구성된 평행사변형
그림 4의 평행사변형의 넓이는 행렬식을 이용해 다음과 같이 쓸 수 있다.
\[det\left(\begin{bmatrix}a & b_1\\ c & b_2\end{bmatrix}\right)\]그런데 재밌는 점은 그림 3의 평행사변형과 그림 4의 평행사변형의 넓이는 같다. 왜냐면 밑변의 길이는 변화가 없고, 두 평행사변형의 높이도 같기 때문이다.
따라서,
\[x_2 \ det\left(\begin{bmatrix}a & b \\ c & d\end{bmatrix}\right)=det\left(\begin{bmatrix}a & b_1\\ c & b_2\end{bmatrix}\right)\]와 같이 쓸 수 있으므로,
\[x_2 = \frac{det\left(\begin{bmatrix}a & b_1\\ c & b_2\end{bmatrix}\right)}{det\left(\begin{bmatrix}a & b \\ c & d\end{bmatrix}\right)}\]와 같다는 것을 알 수 있다. 이것은 $x_1$에 대해서도 같은 방법으로 확인할 수 있다.
그리고, 마지막으로 이 결과는 크래머 공식과 같다는 것을 알 수 있다.