preprequisites
면적분을 이해하기 위해선 다음의 내용에 대해 알고 오시는 것이 좋습니다.
면적분의 수식
우선 면적분의 수식을 바로 적어보자면 다음과 같다.
\[\iint_S\vec{F}\cdot d\vec{S} = \iint_S\vec{F}\cdot\hat{n}dS\]여기서 $\vec{F}$는 벡터장이다. 또, $\vec{S}$는 면벡터로써 쪼개보면 $\hat{n}dS$로 쓸 수 있다. 즉, 크기는 곡면상의 미소 곡면의 넓이($dS$)이고 방향은 법선 벡터($\hat{n}$)인 벡터이다.
면적분의 수식을 잘 살펴보면 벡터장의 선적분의 수식과 굉장히 닮아있다는 것 또한 알 수 있다.
참고로, 벡터장의 선적분의 수식은 다음과 같았다.
\[\int_C\vec{F}\cdot d\vec{r}\]벡터장의 선적분과 면적분의 차이점은 적분해주는 정의역의 범위가 1차원인 곡선인지 아니면 정의역의 범위가 2차원인 곡면인지에 따른 차이라고 할 수 있겠다.
미소곡면의 넓이 dS
식 (1)을 보면 벡터장 $\vec{F}$는 문제에서 주어질 것이고, 미소 곡면의 법선벡터 $\hat{n}$은 저번 article에서 다루었기 때문에 미소곡면의 넓이 $dS$에 대해서만 더 알게된다면 면적분을 계산할 수 있을 것이다.
미소 곡면의 법선 벡터 편에서는 2차원 입력 공간에 대응되는 3차원 출력 공간이 있고 $r(t)$라는 매핑(즉, 함수)에 따라 3차원 곡면이 결정된다고 하였다.
또한, 이 때 아래의 그림 1과 같이 임의의 점 위에서 $u$방향으로의 작은 변화 $du$와 $v$ 방향으로의 작은 변화 $dv$에 대한 변화율은 각각 아래와 같은 벡터로 표현할 수 있다.
\[u\text{의 작은 변화에 따른 } r\text{의 변화율 }\Rightarrow \frac{\partial r}{\partial u} = r_u\] \[v\text{의 작은 변화에 따른 } r\text{의 변화율 }\Rightarrow \frac{\partial r}{\partial v} = r_v\]
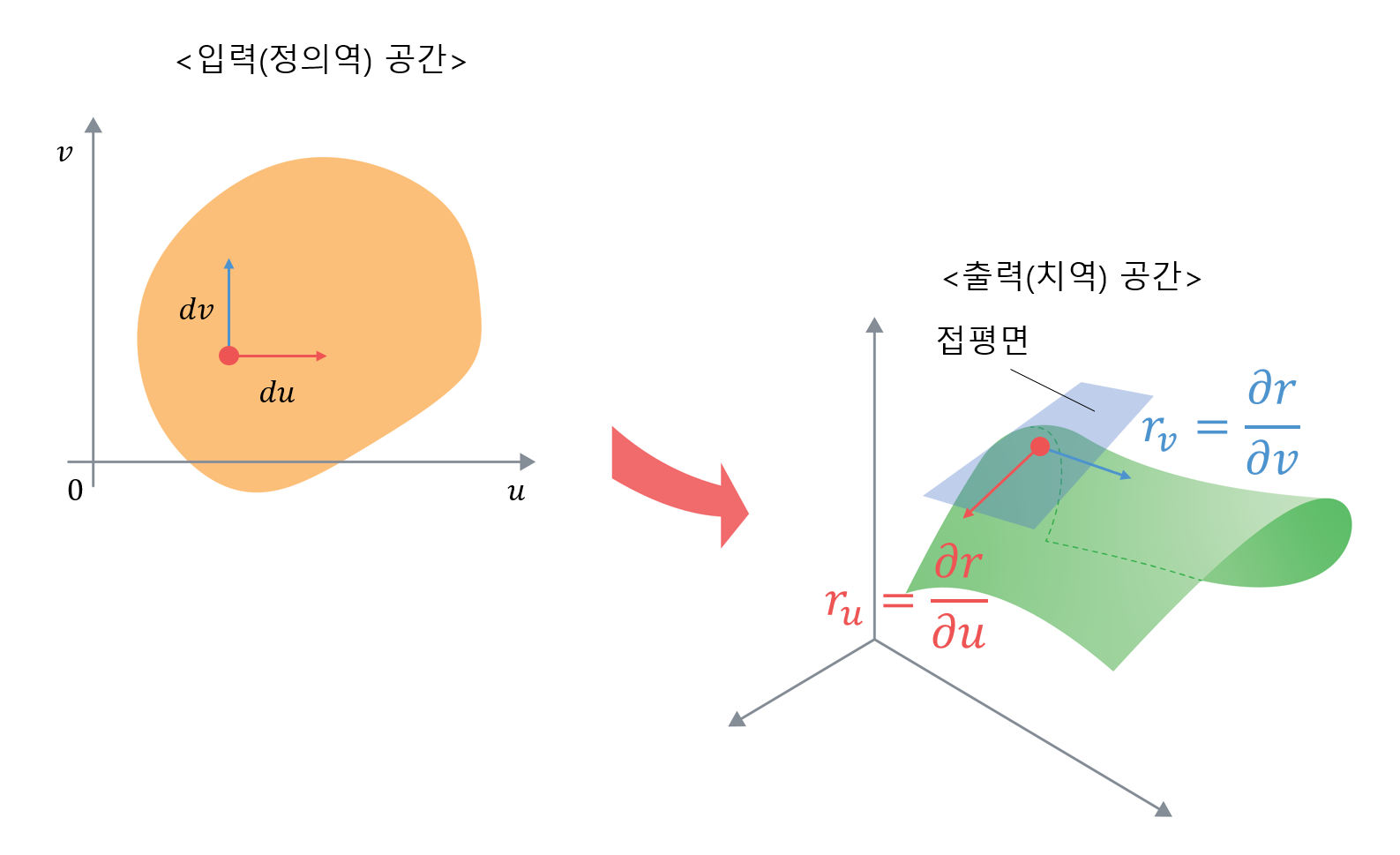
그림 1. 입력 공간의 작은 변화에 따라 얻어지는 출력 공간에서의 변화율
그림 1에서의 논의를 이어 아래의 그림 2와 같이 그림 1에 표시된 벡터들만을 따로 그리면 그림 2와 같다.
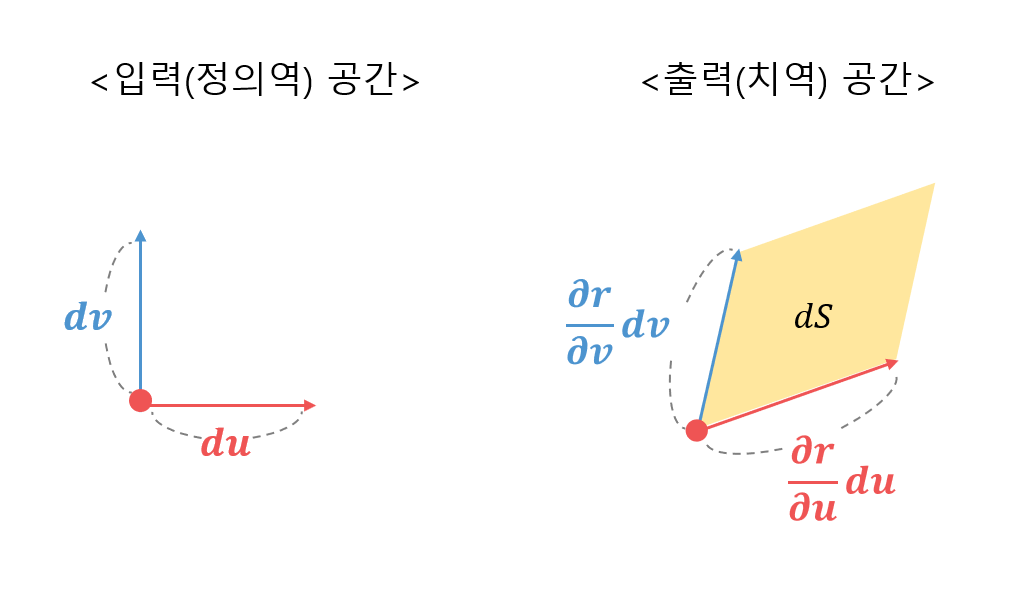
그림 2. 입력 공간의 작은 변화에 따라 얻어지는 출력 공간에서의 변화율
그림 2에서 출력 공간에 해당하는 부분의 그림을 잘 보면 곡면상의 빨간 점에서의 미소 면적 $dS$를 표시해 둔 것을 알 수 있다.
미소면적 $dS$는 $r$ 벡터의 $u$방향으로의 변화에 따른 변화량과 $r$ 벡터의 $v$방향으로의 변화에 따른 변화량을 통해서 얻을 수 있다. 두 변화량에서 편미분으로 표시된 두 개의 값은 모두 벡터이므로 미소면적의 크기 $dS$는
\[dS = \left|\left(\frac{\partial r}{\partial u}du\right)\times\left(\frac{\partial r}{\partial v}dv\right)\right|\]이 때, $du$와 $dv$는 스칼라 값이므로 절대값 기호 밖으로 꺼내주면,
\[=dudv\left|\frac{\partial r}{\partial u}\times\frac{\partial r}{\partial v}\right| = dudv|r_u \times r_v|\]면적분의 식을 다시 전개해보면,
이전 시간에 미소곡면의 법선벡터 $\hat n$은 다음과 같이 쓸 수 있음을 알게 되었다.
\[\hat n = \frac{r_u \times r_v}{|r_u \times r_v|}\]따라서, 식 (1)을 다시 쓰면 다음과 같을 것이다.
\[\iint_S\vec{F}\cdot\hat n dS = \iint_D\vec{F}\cdot \frac{r_u \times r_v}{|r_u \times r_v|}(dudv|r_u \times r_v|) = \iint_D\vec{F}\cdot(r_u \times r_v)dudv\]위 식에서 이중적분 기호의 아랫첨자가 $S$에서 $D$로 바뀐 것은 $u$와 $v$에 대해 적분해주기 때문인데, 그것은 정의역의 영어 표현이 Domain 이기 때문이다.
즉, 치역에서 계산할 것을 정의역에서 계산할 수 있게 식을 변형시켜 주는 것이다.
면적분의 의미: 3D flux
면적분의 값은 미소 곡면의 유량의 의미를 갖는다.
벡터장의 flux(2D)편에서는 미소 경로를 따라 얻을 수 있는 유량에 대해 알아보았는데, 미소 경로에 따른 유량과 미소 곡면에 따른 유량을 비교하면 아래의 그림 3과 같다.
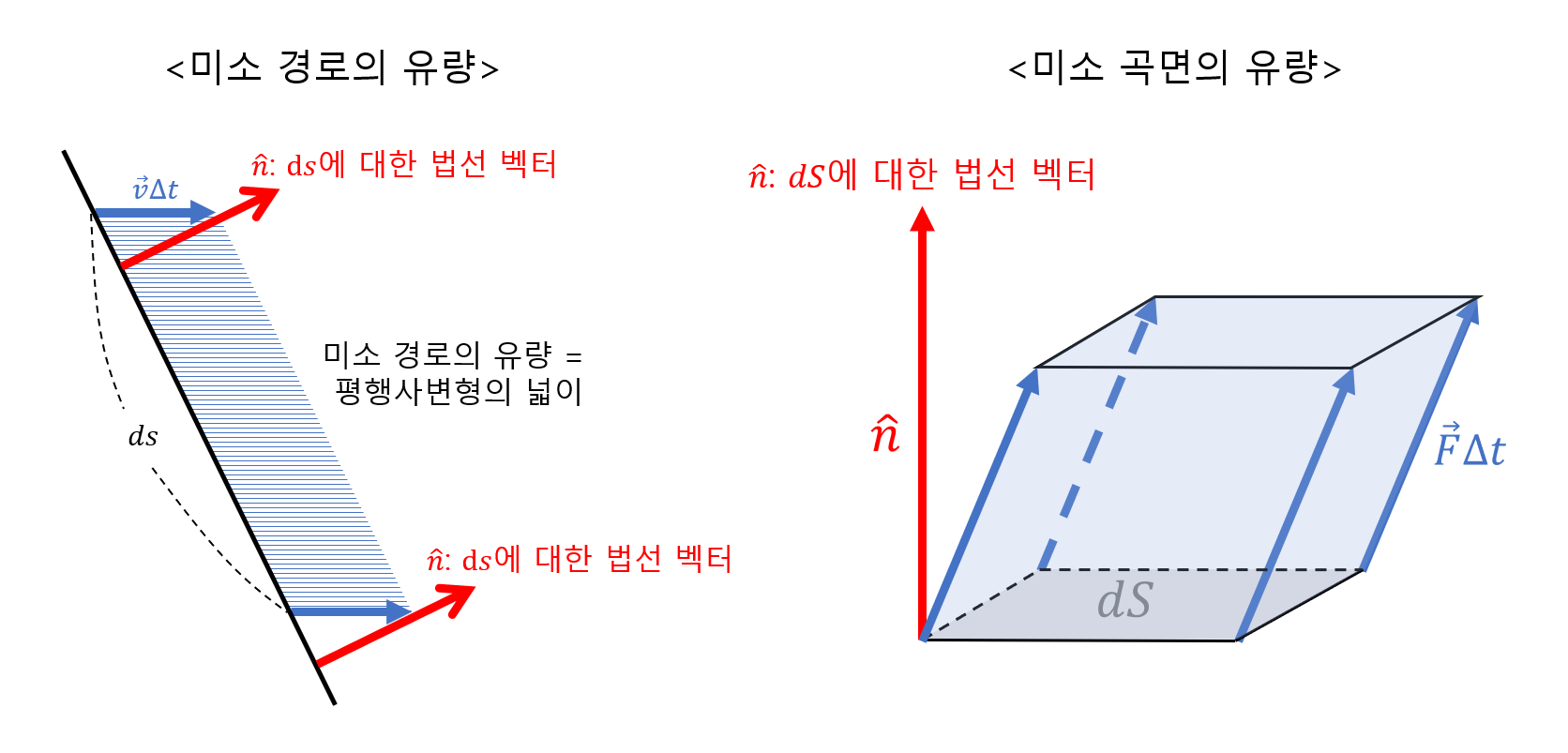
그림 3. 미소 경로의 유량과 미소 곡면의 유량 비교
미소 곡면의 면적 $dS$에 대해서 벡터장 $\vec{F}$가 주어져 있다고 하자.
여기서의 가정은 미소 곡면의 네 변은 매우 길이가 작기 때문에 미소 곡면 상에 있는 벡터장은 모두 같다고 가정해보자.
여기서 유량이라 함은, 벡터장이 물의 유속을 의미한다고 할 때 단위 시간동안 빠져나간 물의 총 양을 의미한다.
$\Delta t$라는 시간동안 물이 빠져나간다고 했을 때 그 물의 양은 그림 3의 우측 그림에서 보는 평행육면체의 부피와 같다.
물이 빠져나가는 속도가 $\vec{F}$이므로 경사면의 길이는 $\vec{F}\Delta t$와 같고, 평행육면체의 높이는 $\vec{F}\Delta t$를 법선벡터 $\hat n$에 내적해줌으로써 얻을 수 있다.
따라서, 물이 시간 $\Delta t$ 동안 빠져나간 총 양은
\[dS\times (\vec{F}\Delta t \cdot \hat n)\]이며, 단위시간동안 빠져나간 물의 양은
\[dS\times (\vec{F}\cdot \hat n) = \vec{F}\cdot \hat n dS\]이다.
이 단위 시간동안 빠져나간 물의 총 양을 모든 곡면에 대해 중적분해주면,
\[\iint_S\vec{F}\cdot \hat n dS\]가 되며 이것은 식 (1)의 면적분과 동일하다.
따라서, 면적분이 의미하는 것은 곡면 $S$를 따라 빠져나간 유량(flux)의 총 양을 의미한다고 할 수 있다.