※ 본 포스팅의 내용은 Thomas Judson의 The ordinary differential equations project에서 많은 부분을 차용하였음을 밝힙니다.

지금까지의 미분방정식에 대한 논의는 주로 1계 미분방정식에 관한 것이었다.

그것도, 1계 1원 미분방정식으로 1원이라는 것은 미분계수가 계산되는 변수가 하나라는 뜻이다. 가령 $t$가 독립변수라고 했을 때, 종속변수는 $x$하나인 경우로 일반적인 식은 다음과 같았다.

\[\frac{dx}{dt}=f(t, x) % 식 (1)\]

하지만, 미분방정식은 종속변수가 하나인 경우에만 한정하여 쓸 수 있는 것은 아니다. 미분방정식 두 개를 한꺼번에 이용하면 두 개 이상의 종속변수에 대한 변화를 한꺼번에 모델링할 수도 있다.

예를 들면, 다음과 같은 연립방정식의 형태를 이용하면 두 개의 종속변수에 대한 변화를 동시에 모델링 할 수 있다.

\[\begin{cases} \dfrac{dx}{dt} = f(x, y) \\\\ \dfrac{dy}{dt} = g(x, y) \end{cases} % 식 (2)\]

포식자-피식자 방정식 (Lotka-Volterra Equation)

생태계를 유지하는 먹이사슬은 밸런스가 아주 중요한 요소이다.

여우에게 잡아 먹히는 토끼는 불쌍해보이지만, 여우도 먹고 살아야하지 않겠냐고 반문하면, 또 그런가 싶기도 한게 자연인지도 모르겠다.

또, 여우가 토끼를 잡아먹는 일은 토끼의 개체수를 유지해주는데 굉장히 중요한 역할을 한다.

토끼는 천적이 없이 가만히 내버려두면 무한정 개체수가 늘어날 것이기 때문이다.

(토지나 먹이의 한계로 인한 개체수 포화에 관한 내용은 이후에 수정된 포식자-피식자 방정식을 통해 확인하자.)

우리는 위의 내용을 미분방정식으로 옮겨 모델링해보고자 한다.

이 유명한 모델링 방정식은 포식자-피식자 방정식 혹은 Lotka-Volterra 방정식이라고 부른다.

우선 토끼(즉, 피식자)의 개체수에 관한 식을 세워보자.

토끼의 개체수를 $R$이라고 하자. 우선 토끼는 가만히 내버려두면 개체수가 기하급수적으로 성장할 것이다.

미분방정식을 이용한 현상 모델링편에서 보았던 것 처럼 여기서는 인구수가 성장하는 모델을 적용할 수 있다.

즉,

\[\frac{dR}{dt}=a R % 식 (3)\]

여기서 $a>0$.

식 (3)에서 추가할 내용은 피식자와 포식자간의 상호작용인데, 토끼의 일부 개체들은 여우 개체수와 상호작용하면서 개체수가 감소한다.

다시 말해, 여우와 만나면 잡아 먹힐 수 있게 된다. 따라서, 식 (3)을 살짝 수정하여 다음과 같이 토끼의 개체수에 대한 방정식을 세울 수 있다.

여우의 개체수를 $F$라고 하면,

\[식(3) \Rightarrow \frac{dR}{dt} = aR -bRF % 식 (4)\]

이다. 여기서 $a, b>0$. 또, 여기서 $RF$는 토끼의 개체수와 여우의 개체수의 곱이며, 상호작용을 나타낸다.

이번에는 여우 개체수의 시간 변화에 대한 방정식을 세워보자.

여우는 가만히 내버려두면 자연스레 개체수가 감소한다고 보자. 풀을 뜯어먹고 여우가 버티기는 어려울 것이다.

즉,

\[\frac{dF}{dt}= -cF % 식 (5)\]

여기서 $c>0$.

그리고, 식 (5)에서 여우와 토끼가 만들어내는 상호작용에 대한 factor도 집어넣으면 수식은 다음과 같이 수정된다.

\[식 (5)\Rightarrow \frac{dF}{dt}=-cF + dFR % 식 (6)\]

여기서 $c, d >0$이고, $FR$은 여우의개체수와 토끼 개체수의 곱이다.

식 (4)와 식 (6)을 한꺼번에 이용하면 토끼와 여우의 개체수가 보여주는 밸런스를 확인할 수 있다.

\[\begin{cases} \dfrac{dR}{dt} = aR -bRF \\\\ \dfrac{dF}{dt} = -cF + dFR \end{cases} % 식 (7)\]

위의 식을 정확히 풀어 닫힌 형식으로 해(solution)을 얻어내는 방법은 아직도 알려져 있지 않다 ^{1 2}.

하지만, 우리에게 당장 그것보다 더 중요한 것은 이 solution의 형태가 어떤 식으로 작동하며, 식 (7)의 모델링이 현상을 잘 반영하는지 체크하는 일이다.

식 (7)에서 $a=2, b= 1, c = 5, d = 1$라고 이라고 놓고 피식자와 포식자 각각의 solution curve를 그려보면 다음과 같다. 여기서 초기값은 피식자와 포식자 모두 1로 두었다.

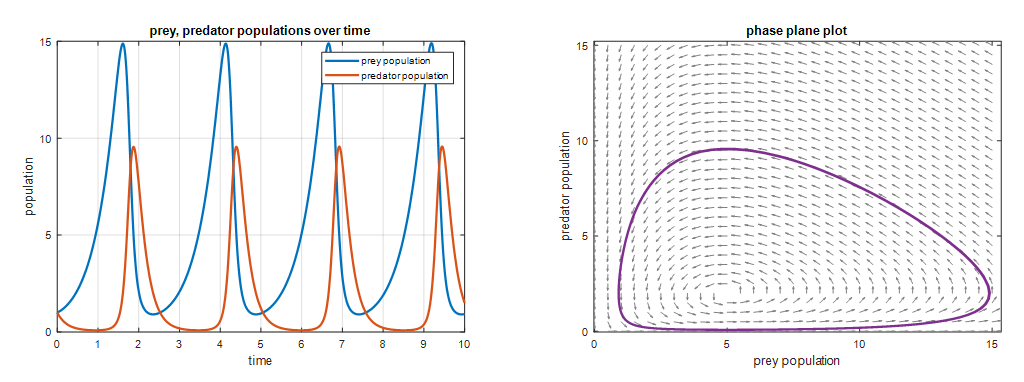
그림 1. 포식자-피식자 모델의 solution curve 중 하나

그림 1의 왼쪽을 보면 상대적으로 피식자(파란색)는 빠르게 성장해간다. 처음에는 포식자(빨간색)가 잡아먹을 피식자가 적다보니 포식자 개체들이 자연사하는 경우도 많지만,

피식자가 자연 번식이 충분히 이루어지고 나면 그 뒤부터는 포식자가 잡아먹을 피식자들이 많이 생기는 것으로도 볼 수 있으므로 포식자들의 개체수도 늘어나게 된다.

time = 2 즈음에 보면 포식자의 수가 너무 늘어날 때 쯤이 되면 피식자들이 감소하게 되는데, 이는 잡아먹혀서 죽는 일들이 더 많아졌기 때문일 것이다.

그림 1의 오른쪽에는 피식자와 포식자의 관계를 x y 평면에 한번에 나타냈다. 초기값은 (1,1)이므로 (1,1)이라는 점에서 시작하면 화살표를 따라가면서 보라색 커브가 그려지는 것으로 볼 수 있는데,

처음에는 피식자의 수만 증가하다가 서서히 포식자가 늘어나면서 피식자가 감소하는 것을 볼 수 있다.

포식자-피식자 모델은 이렇듯 포식자-피식자 간의 개체수가 시간에 따라 어떻게 변하는지를 보여주고 있는 모델이라고 할 수 있다.

한계 수용량이 정해진 포식자-피식자 모델

이번에는 앞서 확인한 포식자-피식자 모델을 살짝 수정하여 한계 수용량이 있는 경우의 모델을 살펴보자.

이 내용은 미분방정식을 이용한 현상 모델링에서 보았던 logistic growth의 맥락을 그대로 차용한 것이다.

다시 말해, 이번 모델에서는 토끼가 먹을 수 있는 풀의 양이 한정적이라는 것이다. 무한히 넓게 펼쳐진 초원이 아닌 한정된 양의 풀이 있는 초원에서 토끼가 성장하게 되면 토끼의 성장량은 한계가 있을 수 밖에 없다.

logistic growth의 식을 이용해 식 (7)에서 토끼의 개체수 성장에 관한 식을 수정해보자.

\[식(7)\Rightarrow \begin{cases} \dfrac{dR}{dt} = aR(1-\dfrac{R}{N}) -bRF \\\\ \dfrac{dF}{dt} = -cF + dFR \end{cases} % 식 (8)\]

여기서 $N$은 한계 수용량이다.

앞선 분석에서와 마찬가지로 $a=2, b= 1, c = 5, d = 1$로 하고, $N=10$으로 했을 때의 solution curve를 그려보면 다음과 같다.

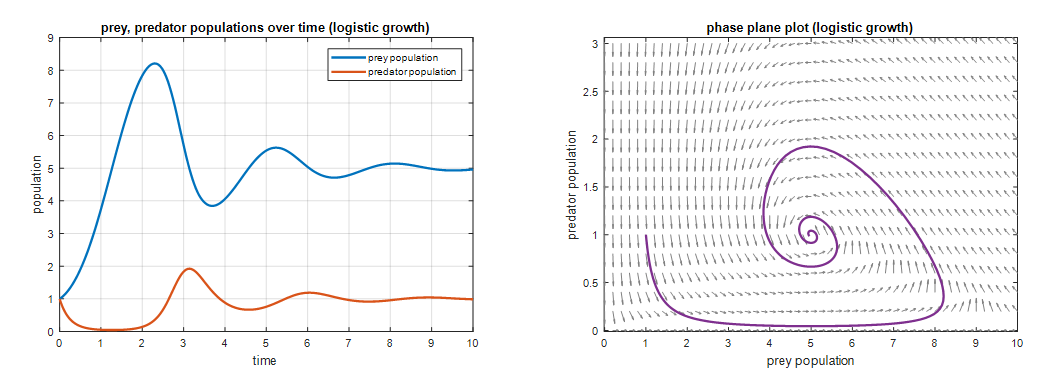
그림 2. 한계 수용량이 정해진 포식자-피식자 모델의 solution curve 중 하나

그림 2의 왼쪽을 보면 각 개체의 개체수가 각각이 수렴하는 값이 있는 것을 볼 수 있다.

이것은 그림 2의 오른쪽의 phase plot을 보면 더 확실히 보이는데, 대략 prey:predator 의 비율이 5:1 정도인 지점으로 값이 solution이 수렴하게 된다는 걸 알 수 있다.

거기다, 그림 2의 오른쪽에서 볼 수 있듯이 한계 수용량이 정해진 경우의 포식자-피식자 모델에서는 5:1 비율의 주변 값에서는 어떤 초기 조건으로부터 출발하더라도 5:1 비율로 개체수가 수렴하게 되는 것을 볼 수 있다.

Damped harmonic motion

연립 미분방정식의 관점을 통해 미분방정식을 이용한 현상 모델링 편에서 보았던 또 다른 내용 중 하나인 damped harmonic motion을 알아보자.

damped harmonic motion의 식은 다음과 같았다.

\[m\frac{d^2x}{dt^2}+b\frac{dx}{dt}+kx = 0\]

이 식은 2계 미분방정식이지만 다음과 같이 처리하면 2원 1계 연립미분방정식으로 고쳐쓸 수 있다.

새로운 변수 $v$를 다음과 같이 설정하자.

\[v = \frac{dx}{dt}\]

그러면 $v$의 미분은

\[\frac{dv}{dt}=\frac{d^2x}{dt^2}=-\frac{b}{m}v-kx\]

이다.

한편, 우리가 보고자 하는 것은 식 (7)과 유사한 것인데, 다시 말하면 좌변에는 두 변수에 대한 미분 계수가 들어가야 하고, 우변에는 두 변수에 대한 수식이 들어가는 것이다.

즉, 좌변을 $x’$과 $v’$이라고 놓으면,

\[\begin{cases} \dfrac{dx}{dt} = v \\ \\ \dfrac{dv}{dt} = -\dfrac{b}{m}v-kx \end{cases}\]

와 같이 모델링 할 수 있다.

여기서 $b/m$을 0.4, $k$를 1.04라 두고, 초기값을 $x=0$, $x’ = 2$로 두었을 때 solution curve와 phase plane은 아래의 그림과 같다.

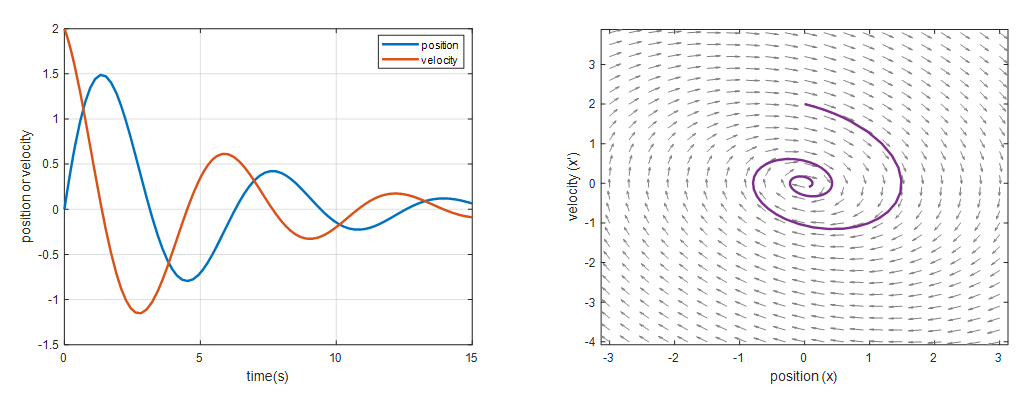
그림 3. damped harmonic motion (underdamped)의 solution curve와 phase plane

phase plane에서 시간에 따른 위치의 변화를 진자운동 애니메이션으로 표현하면 아래와 같이도 볼 수 있다.

그림 4. damped harmonic motion (underdamped)의 phase plane과 진자 운동으로 표현한 animation

위의 애니메이션을 보면 알 수 있듯이 진자 움직임은 진동이 서서히 느려지되, harmonic motion의 힘만큼 강하게 damping이 된 것이 아니다 보니 여러 주기를 반복해가면서 서서히 느려지는 경우에 대해 모델링 한 것이라고 할 수 있다.