Prerequisites
이 포스트를 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
전반적인 내용
이번 article에서 정리하게 될 내용은 대략적으로 다음과 같다.
- 검정 통계량이란 무엇인가?
- t-value의 의미
- 모집단에서 수 차례 표본 추출을 해보고 그들의 t-value를 계산하여 분포를 직접 확인
검정 통계량(test statistic)
스튜던트의 t-test에 대해 이해하기 전에 검정 통계량이라는 개념에 대해서 한번은 짚고 넘어가는 것이 좋을 것 같다.
$\lt$표본과 표준 오차의 의미$\gt$편에서는 모집단, 모수, 표본, 표본 통계량에 대해서 알아보았고 마지막으로 표본 통계량은 추정치이므로 추정 오차가 발생하며 그것을 표준 오차(Standard Error)라고 부른다는 것을 공부해보았다.
그렇다면 검정 통계량이란 무엇일까?
검정 통계량은 우리가 흔히 “통계적으로 비교 분석한다”라고 하면 사용하는 $t, F, z, \chi^2$ 등의 개념을 통칭하는 것인데,
어렵게 생각할 것 없이 검정 통계량은 “통계적 가설의 진위 여부를 검정하기 위해” 표본으로 부터 계산하는 통계량이다.
즉, 검정 통계량은 표본 통계량을 2차 가공한 것으로 생각하면 편한데, 통계적 가설 진위 여부를 검정한다는 것은 검정통계량의 값이 기준을 벗어나는지 확인하여 세워둔 가설이 틀렸다고 할 수 있는지 확인하는 과정이다.
이렇게 말하더라도 와닿지 않을 수 있는데, 이번 article에서는 t-value를 중심으로 검정 통계량에 대해 이해해보도록 하자.
t-value의 의미: 차이 / 불확실도
조사 혹은 연구를 진행하다보면 두 표본 집단 간의 차이를 비교해야 할 때가 생길 수 있다. 표본 집단간의 차이를 비교할 때에는 여러가지 방법을 사용할 수 있겠으나, 주로 비교되는 지표는 평균이다.
가령, 신약을 개발한 뒤 약의 효과를 확인해보고 싶다면 어떤 실험을 계획할 수 있을까?
우선 임상적으로 문제가 없는 사람들을 최대한 “많이” 모은 뒤, 그들을 두 그룹으로 최대한 “랜덤하게” 나눈 다음, 한 그룹에는 플라시보 약을 주고 한 그룹에는 새로 개발한 약을 준 다음 약효를 확인하면 될 것이다.
그 결과 각 그룹에서 평균 수치를 얻을 수 있다면, 그 두 평균값의 차이를 확인하면 통계적으로 비교한 것으로 볼 수 있을까? 아니다. 이 두 평균값은 표본 평균인데, 이 두 표본 평균들은 오차를 항상 수반하고 있다는 사실을 잊어선 안된다. 다시 말해 표본 평균이기 때문에 발생하는 오차를 염두하면서 두 표본 그룹의 평균 차이에 관한 지표를 만들어야 한다. 우리는 표본 통계량의 불확실도에 대해 배운 바 있으며 이것을 표준 오차라고 한다고 배운바 있다.
따라서 차이에 불확실도를 나누는 방식으로 통계적 차이 지표를 만들면 되는 것이다.
표본 평균 차이의 통계적 지표: 차이 / 불확실도
여기서 말하는 불확실도는 두 표본그룹의 평균간 차이의 불확실도를 의미한다.
t-value의 의미는 위에서 확인한 ‘통계적 지표’와 같은 의미를 가진다. 즉, t-value가 말하는 것은 “이 정도 차이나고~! 그러면서 오류는 이정도야~!”라고 할 수 있다.
수학적으로 t-value를 정의해보자.
두 표본 그룹간의 차이는 $\bar{X_1} - \bar{X_2}$로 쓰면 좋겠고, 위에서 말한 불확실도는 두 표본 그룹간의 평균 차이에 관한 것이며 수학적으로는 표준오차로 생각할 수 있으므로 $s_{\bar{X_1} - \bar{X_2}}$로 쓸 수 있다.
이 ‘차이의 지표’에 $t$라는 이름을 붙이면 그림 1과 같은 식으로 쓸 수 있다.
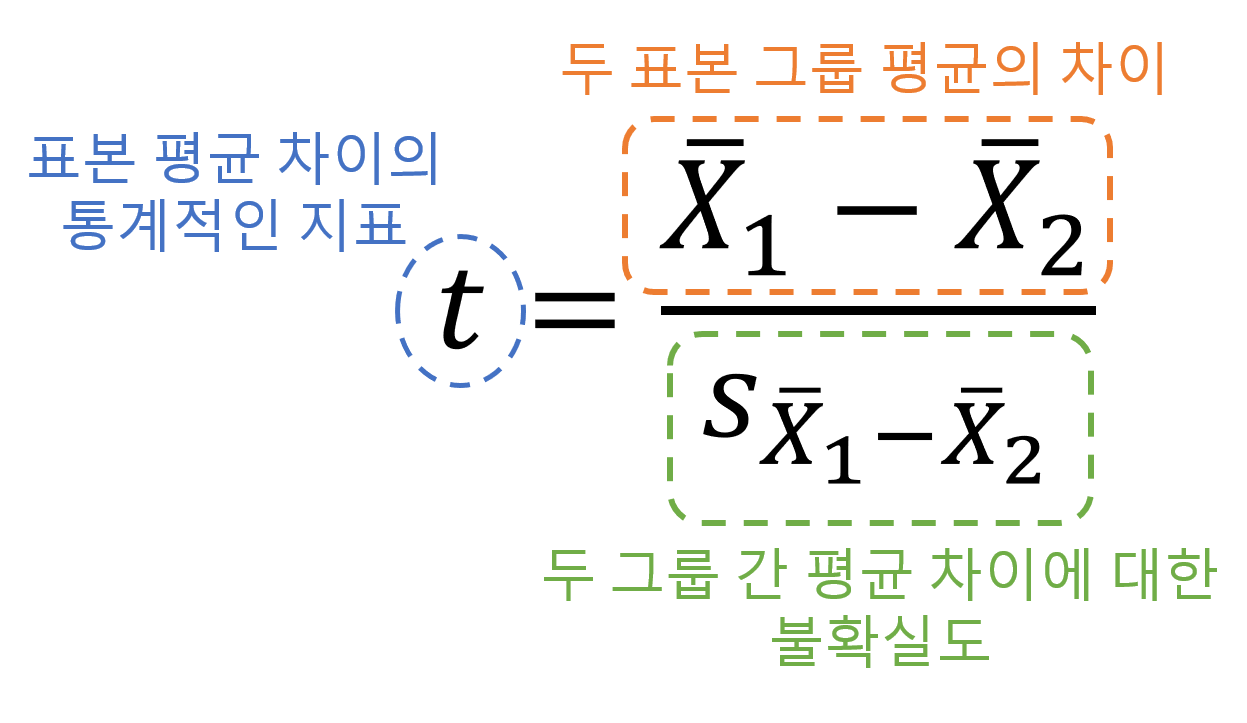
그림 1. t-value의 구성 성분과 그 의미
조금 더 식을 구체화시켜보면 다음과 같이 써나갈 수 있을 것이다.
\[t = \frac{\bar{X_1} - \bar{X_2}}{s_{\bar{X_1} - \bar{X_2}}}\]여기서 $s_{\bar{X_1} - \bar{X_2}}$에 대해서 조금 더 풀어서 생각해보자.
\[s_{\bar{X_1} - \bar{X_2}} = \sqrt{Var\left[{\bar{X_1} - \bar{X_2}}\right]}\]이고,
\[Var\left[{\bar{X_1} - \bar{X_2}}\right]\] \[= Var[\bar{X_1}] + Var[\bar{X_2}]\] \[= \frac{Var[X_1]}{n_1} + \frac{Var[X_2]}{n_2}\] \[= \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}\]이다.
여기서 식 (3)에서 식 (4)로 넘어갈 때에는 두 그룹의 평균 값들은 독립적으로 계산된다고 볼 수 있으므로 두 그룹 간 차이에 관한 분산이 각 그룹의 분산의 합으로 계산된 것이다. 또, 식 (4)에서 식 (5)로 넘어갈 때에는 다음과 같은 방식으로 계산되었다.
식 (4)에서
\[\bar{X}_1 = \frac{1}{n_1}\sum_{i=1}^{n_1}X_i\]이므로
\[Var[\bar{X}_1] = Var\left[\frac{1}{n_1}\sum_{i=1}^{n_1}X_i\right]\]여기서 $Var[aX]=a^2Var[X]$ 이므로,
\[= \frac{1}{n_1^2}Var\left[\sum_{i=1}^{n_1}X_i\right]\] \[=\frac{1}{n_1^2}Var\left[X_1+X_2+\cdots+X_{n_1}\right]\]여기서 $Var[X\pm Y] = Var[X] + Var[Y]$ 이므로,
\[=\frac{1}{n_1^2}\left(Var[X_1]+Var[X_2]+\cdots+Var[X_{n_1}]\right)\]여기서 $Var[X_1] = Var[X_2] = \cdots = Var[X_n] = s_1^2$ 이므로,
\[=\frac{1}{n_1^2}\times n_1\times s_1^2 = \frac{s_1^2}{n_1}\]따라서, 식 (7)~(12)과 같은 방식을 $\bar{X_2}$에도 적용하면,
\[s_{\bar{X_1} - \bar{X_2}} = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\]로 쓸 수 있다.
따라서 식(1)은 다시 쓰면 다음과 같다.
\[식(1) = \frac {\bar{X_1} - \bar{X_2}} {\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}\]t-value의 여러가지 variation
식(1) 혹은 식(14)로 표현되는 t-value는 실험 상의 가정이나 세팅에 따라 여러가지 변형이 존재하는데 결국은 “pooled standard deviation을 사용하는가?”가 핵심이다.
pooled standard deviation (혹은 pooled variance)라는 것은 두 집단의 표준편차가 같다고 가정하고 하나의 표준편차 값으로 두 집단의 표준 편차를 대체하겠다는 의미를 갖는다.
두 집단의 표준편차(혹은 분산)이 같은 경우에 대해서 (즉, pooled standard deviation을 사용한다고 했을 때), 두 가지의 케이스를 생각해볼 수 있다.
첫번째로 두 표본 집단의 n 수가 $n_1=n_2=n$으로 동일하고 두 표본 집단의 분산이 같다고 가정할 수 있는 경우에는 다음과 같이 $s_{\bar{X_1} - \bar{X_2}}$을 쓸 수 있다.
\[식(1) \Rightarrow \frac{\bar{X_1} - \bar{X_2}} {\sqrt{\frac{s_p^2}{n}+\frac{s_p^2}{n}}} =\frac {\bar{X_1} - \bar{X_2}} {s_p\sqrt{\frac{2}{n}}}\quad\text{where}\quad s_p=\sqrt{\frac{s_1^2+s_2^2}{2}}\]즉, 식(15)은 식(14)에서 $s_1$과 $s_2$를 $s_p$로 대체한 것으로 $s_p$는 pooled standard deviation을 나타내고 있다.
두 번째로 두 표본 집단의 n수는 다르지만 두 표본 집단의 분산은 같다고 가정할 수 있는 경우에는 t-value를 다음과 같이 쓸 수 있다.
\[식(1) \Rightarrow \frac{\bar{X_1} - \bar{X_2}} {\sqrt{\frac{s_p^2}{n_1}+\frac{s_p^2}{n_2}}} = \frac {\bar{X_1} - \bar{X_2}} {s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}\quad\text{where}\quad s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\]식 (15), (16)의 수식은 복잡해 보이지만 사실은 표준 편차값을 pooled 처리 할 것이냐 아니냐에 따라 달린 문제이므로, 실제 연구나 분석에서 적용할 때에는 그 상황에 맞게 적절한 수식을 이용하면 될 것이다.
그냥 표준편차로만 나누면 안되나?
식 (14)~(16)를 보면 그림 1에서 표현한 것에 비해서 식이 꽤 복잡해 보이고, 특히나 정규분포의 식 $z=\frac{\bar{X}-\mu}{\sigma }$에 비해 $n$이라는 값이 복잡하게 들어가있어서 식 (14)~(16)만을 봤을 때에는 t-value에 대해 이해하기 어렵다.
왜 t-value에는 $n$이 포함되어야 할까?
그 이유는 아래의 그림2를 보면 잘 이해할 수 있다.
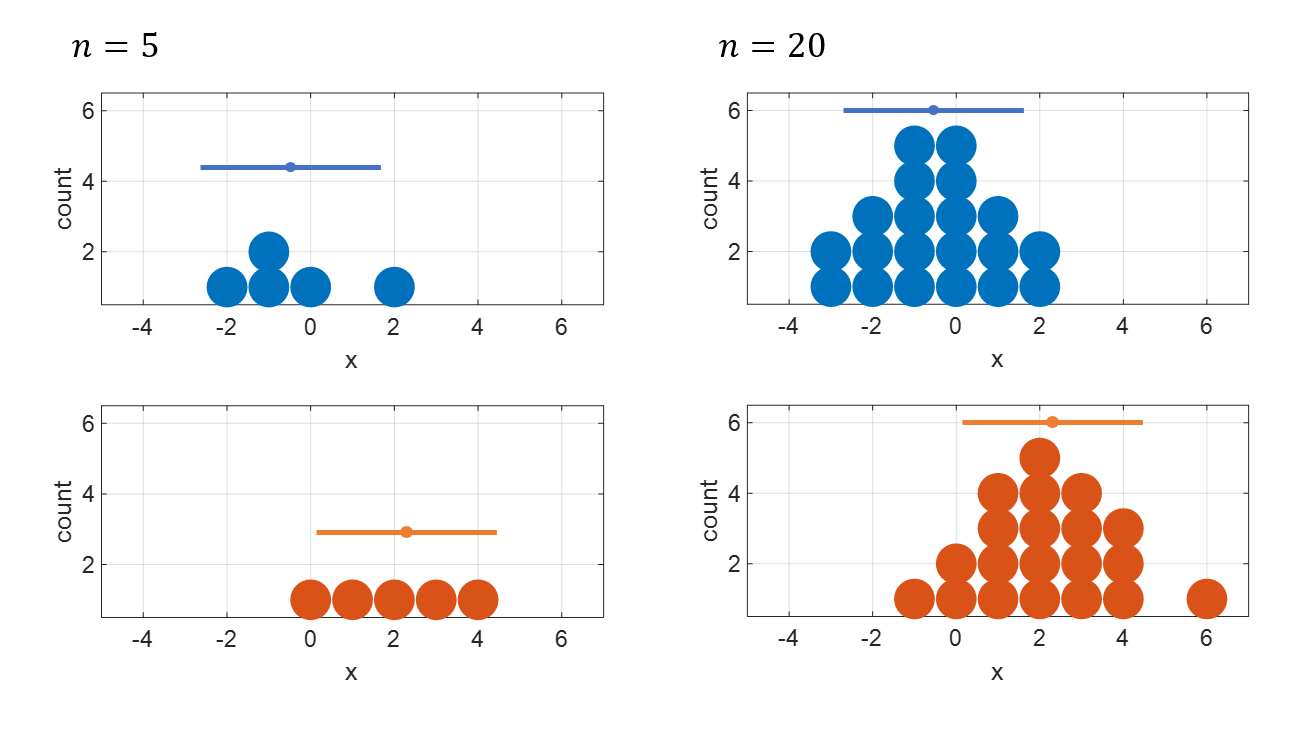
그림 2. 표본의 크기가 클 수록 두 표본의 평균 값을 더 확실히 계산할 수 있다.
즉, 표본의 크기가 클 수록 표본 평균에 대한 표준 오차가 작아진다.
그림 2를 보면 알 수 있듯이 표본의 크기(즉, n수)가 클 수록 두 표본의 평균 값을 더 확신을 갖고 계산할 수 있다. 그림 2의 좌측의 두 개의 그룹과 우측의 두 개의 그룹을 비교할 때를 생각해보면 쉽게 이해할 수 있다.
여기서 “확신을 갖고”라는 표현은 매우 비-수학적인 것처럼 느껴질 수 있는데, 조금 더 수학적으로 서술하자면 표본의 크기가 클 수록 표본 평균에 대한 표준 오차가 작아지기 때문에 더 “확신을 갖고” 계산할 수 있다.
충분히 큰 t-value의 기준은 어떻게 정해지는가?
이번 article의 초반부 “검정 통계량” 꼭지에서 언급했듯이 검정 통계량 중 하나인 t-value는 표본 통계량을 2차 가공한 것과 다를바가 없다.
표본과 표준오차의 의미편에서 표본 평균의 분포를 계산한 것과 같이 모집단에서 임의의 두 개의 표본 집단을 추출하고 t-value를 계산할 수 있다. 모집단의 수가 150이고 n=6인 표본 그룹 두 개를 추출하는 과정을 총 100번 반복하면서 t-value의 분포를 확인해보자.
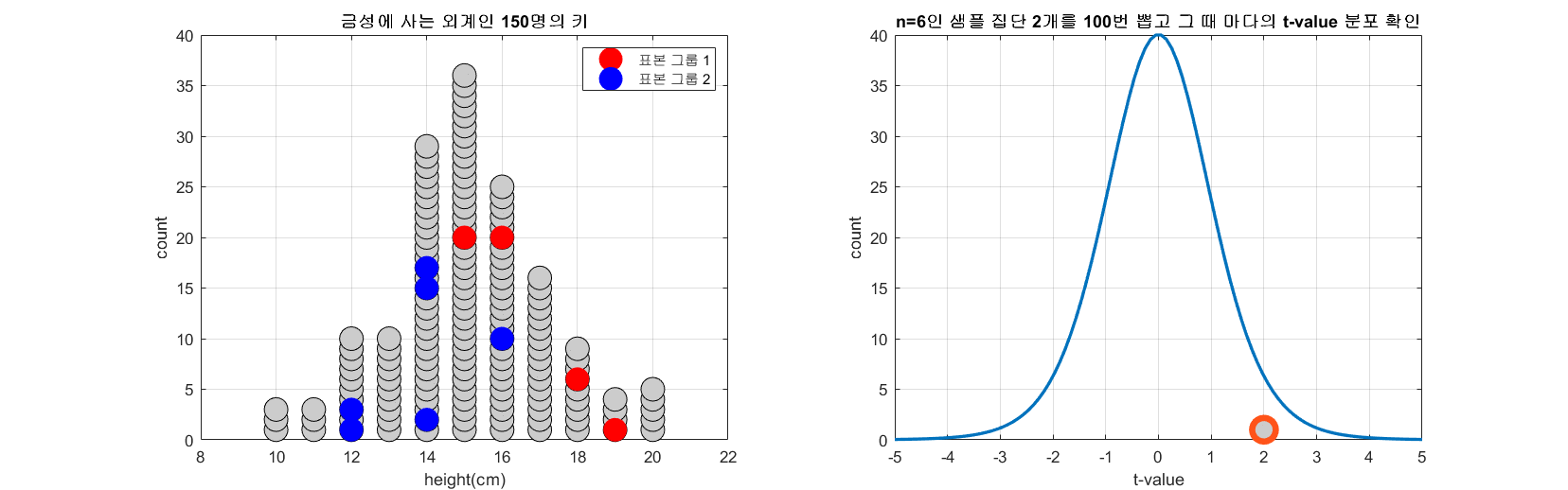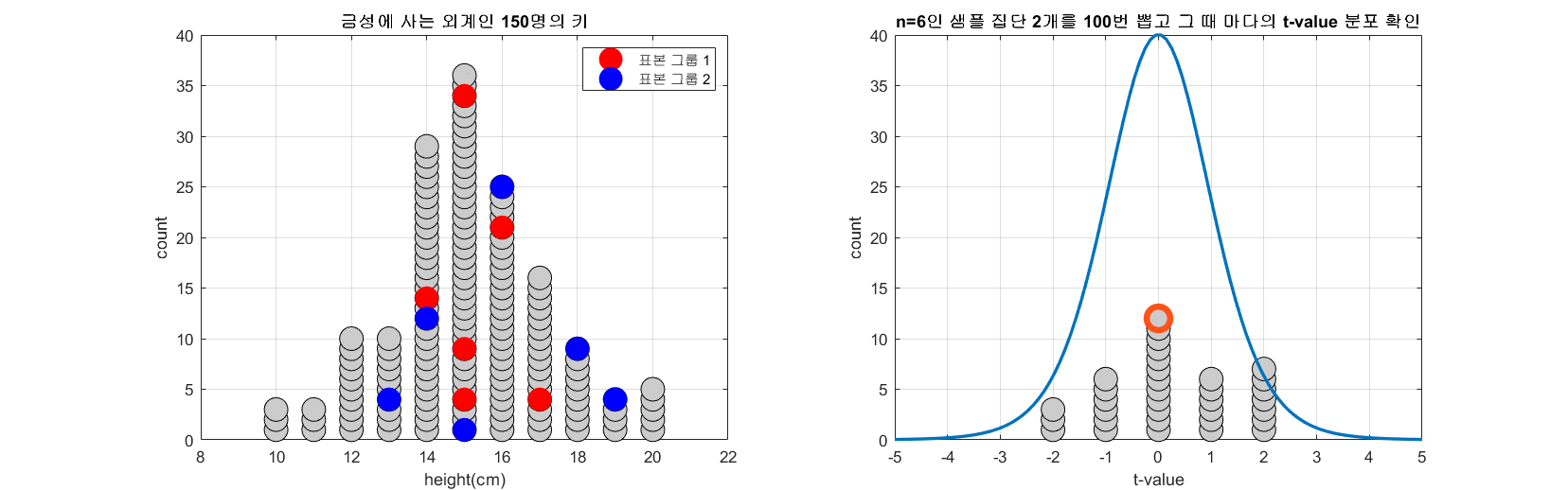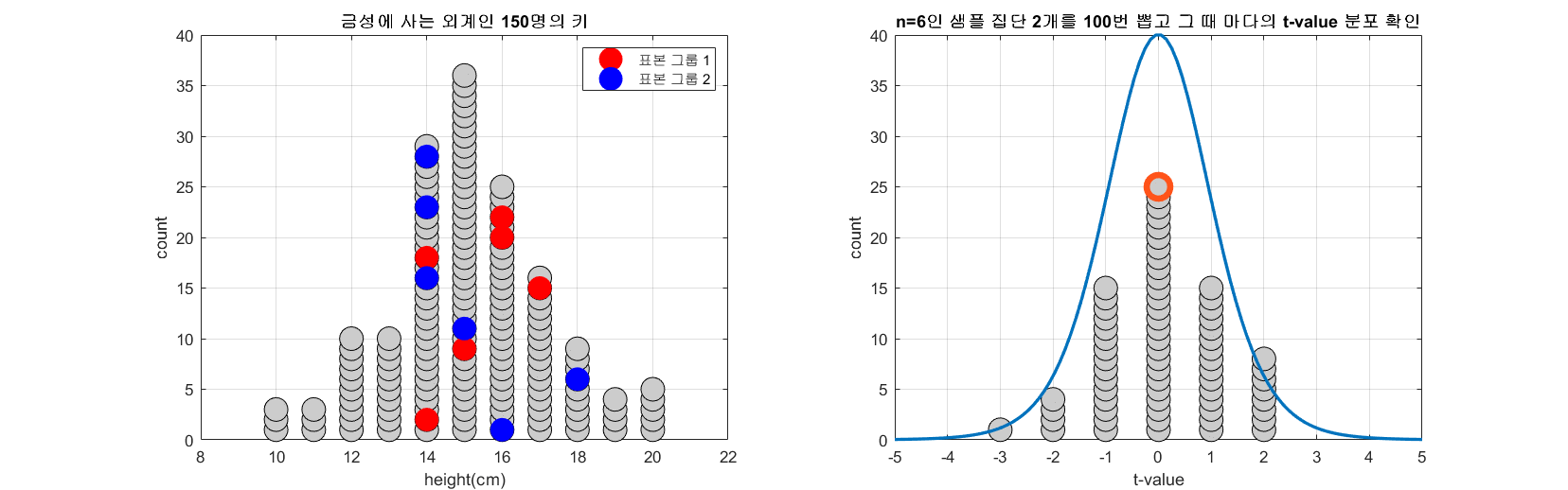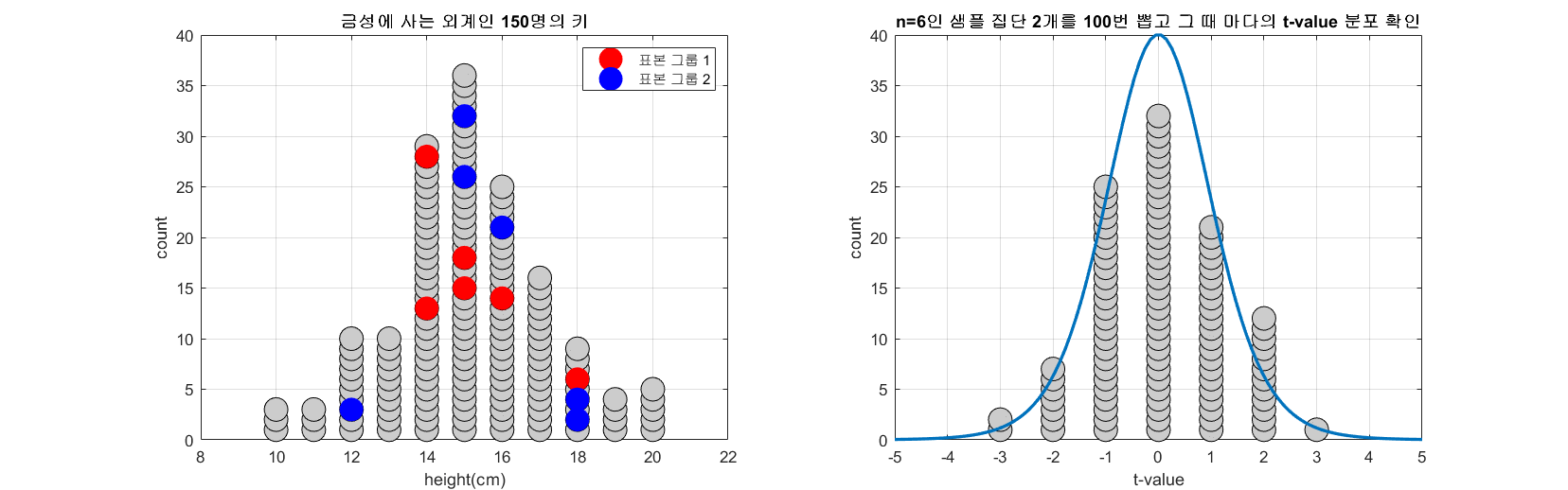
그림 3. 100 번 n=6인 두 개의 표본 그룹을 추출해보고 그 때 마다 얻게되는 t-value를 그린 것
그림 3의 과정을 잘 보면, 하나의 모집단에서 두 개의 표본 그룹을 추출해서 t-value를 구하면 많은 경우 t-value는 0에 가깝게 계산되지만 어쩌다 가끔씩 하나의 모집단에서 계산된 t-value임에도 불구하고 2, 3 과 같은 값을 가지는 t-value가 계산되기도 한다.
즉, 두 표본 집단으로부터 충분히 큰 t-value가 계산되었다는 사실이 말해주는 것은 다음과 같다.
두 표본집단이 하나의 모집단에서 나왔다고 가정했을 때 이런 큰 t-value가 나왔을 확률은 매우 낮으므로, 이 두 표본집단이 하나의 모집단에서 나왔을 것이라는 가정이 맞을 확률 또한 매우 낮다고 말할 수 있다.
사실 그림 3에서와 같은 샘플 추출 과정은 100번이 아니라 거의 무한하다 싶을 정도로 많은 경우의 수가 있을 수 있는데, 모집단의 수가 150이고 n=6인 표본 집단 두 개를 뽑는다고 했을 때 가능한 경우의 수는
\[_{150}C_{12} = 172,420,656,389,440,550\notag\]가지나 된다.
이처럼 수많은 경우의 수에 대해 표본 추출을 할 수는 없으므로, 수학적으로 t-value들의 분포를 계산하여 공식화 한 것이 t-분포(그림 3 우측에서 실선)라고 할 수 있다.
참고문헌
- Primer of biostatistics 6th edition, Stanton A Glantz, McGraw-Hill Medical Publishing Division