
KL divergence가 말하는 것: 이상과 현실 간의 괴리
prerequisites
해당 포스팅의 내용에 대해 이해하시려면 아래의 내용에 대해 알고 오시는 것을 추천드립니다.
크로스 엔트로피(cross entropy)
본 포스팅의 주제인 KL-divergence에 대해 설명하기에 앞서 KL divergence를 이해하기 위해 꼭 필요한 개념인 크로스 엔트로피에 대해 먼저 알아보고자 한다.
크로스 엔트로피는 한마디로 하면 ‘예측과 달라서 생기는 깜놀도(즉 정보량)’라고 할 수 있다.
이를 조금 더 자세하게 알기 위해 우선 출력가능한 결과물이 두 가지인 경우(binary case)에 대해서부터 알아보도록 하자.
Binary case의 크로스 엔트로피
binary case에서는 출력이 0 혹은 1의 두 가지 경우만 있을 수 있다.
어떤 데이터에 대해서 목표값과 모델의 출력값 두 가지의 값을 생각할 수 있다고 해보자.
가령, 어떤 데이터(키, 몸무게 등…)를 주고 ‘남자’ 혹은 ‘여자’로 판별하라고 했을 때 각각의 판별 결과를 0 혹은 1로 출력할 수 있다.
binary case의 cross entropy는 다음과 같이 정한다.
target이 $y$ 이고 예측값이 $\hat{y}$일 때,
\[BCE = -y\log(\hat y) - (1-y) \log(1-\hat y)\](BCE: Binary Cross Entropy)
타겟값과 모델 출력값은 모두 0 혹은 1일 수 있으므로 총 네 가지의 경우가 있을 수 있다.
① $y=1$, $\hat y = 1$ 인 경우
이 경우는 타겟값을 정확히 모델이 맞추었는데, BCE 값을 보면 0이 출력됨을 알 수 있다.
\[BCE = -y\log(\hat y) - (1-y) \log(1-\hat y)\notag\] \[=1\cdot \log(1) - 0 \cdot \log(0) = 0\]② $y=1$, $\hat y = 0$ 인 경우
이 경우는 타겟값을 맞추지 못했다. 이 때 BCE의 값은 $\infty$인 것을 알 수 있다.
\[BCE = -y\log(\hat y) - (1-y) \log(1-\hat y)\notag\] \[=-1\cdot \log(0) -0\cdot \log(1) = \infty\]③ $y=0$, $\hat y = 1$인 경우
위의 경우와 마찬가지로 타겟값을 맞추지 못했고, BCE의 값은 마찬가지로 $\infty$이다.
\[BCE = -y\log(\hat y) - (1-y) \log(1-\hat y)\notag\] \[=-0\cdot \log(1) - (1)\cdot\log(0) = \infty\]④ $y=0$, $\hat y = 0$인 경우
타겟 값을 정확히 맞춘 경우로 BCE의 값은 0이 된다.
\[BCE = -y\log(\hat y) - (1-y) \log(1-\hat y)\notag\] \[=-0\cdot\log(0) - (1)\log(1) = 0\]여러가지 출력 case를 가지는 경우의 Cross Entrpy
Binary Cross Entropy에 대해서 보았을 때 알 수 있는 것은 Cross Entropy는 타겟값과 모델의 출력값이 얼마나 다른지를 표현한 것임을 알 수 있다.
즉, BCE의 식은 이렇게도 쓸 수 있다.
\[BCE = \sum_{x\in{0, 1}}\left(-P(x)\log(Q(x))\right)\]여기서 $P(x)$는 희망하는 타겟에 대한 결괏값이고, $Q(x)$는 모델에서 출력한 출력값이라고 볼 수 있는 것이다.
이를 조금 더 일반화하면, 다음과 같이 여러가지 출력 case를 갖는 경우에 대한 cross entropy를 정의할 수 있을 것이다.
\[CE = \sum_{x\in\chi}\left(-P(x)\log(Q(x))\right)\]위의 Cross Entropy 식을 통해서 우리가 생각할 수 있는 것은 무엇인가?
그것은 CE는 $Q$라는 모델의 결과에 대해 $P$라는 이상적인 값을 기대했을 때 우리가 얻게되는 ‘놀라움’에 대한 값을 정보량으로 표현한 것이라는 점이다.
예를 들어, 아래와 같이 약간은 비정상적인 주사위를 굴린다고 해보자.
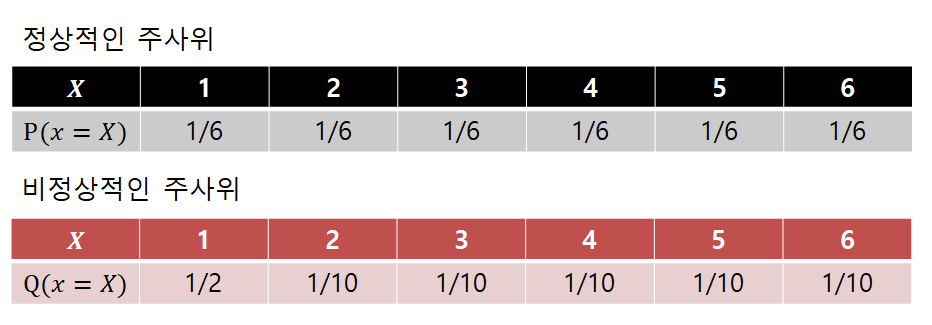
그림 1. 이상적인(혹은 정상적인) 주사위와 비정상적으로 1의 횟수가 많이 나오는 주사위에 대한 확률 분포
즉, 이 예시가 말하는 것은 모든 눈금에 대한 확률이 1/6인 정상적인(혹은 이상적인) 주사위와 다르게 우리가 갖고 있는 이 이상한 주사위(우리의 모델)을 굴렸을 때
우리가 얻게 되는 ‘놀라움의 정도’가 얼마나 될지 알아보자는 것이다.
Cross Entropy를 계산하면,
\[\Rightarrow -\sum_i P(x_i)\log(Q(x_i)) = -\left(\frac{1}{6} \log_2(1/2) + \frac{5}{6} \log_2(1/10)\right) = 2.9349 \text{ bit}\]인데 반해, 정상적인 주사위였다면 정보 엔트로피 값은
\[\Rightarrow -\sum_i P(x_i)\log(P(x_i)) = -\left(\frac{6}{6}\log_2(1/6)\right) = 2.5850 \text{ bit}\]이다.
즉, 이상적으로 생각하고 있는 주사위를 기대하고 우리가 얻은 주사위의 실제 값을 이용해 Cross Entropy를 계산하면 그 놀라움의 정도(즉, 이상과 현실과의 괴리에 대한 놀라움)는 더 크다고 할 수 있다.
KL divergence: 정보 엔트로피의 상대적 비교
KL divergence는 쿨백-라이블러(Kullback-Leibler) 발산을 줄여서 쓴 말인데, 쿨백과 라이블러 모두 사람이름인 것으로 확인된다.
그러니까, KL divergence를 생각할 때는 “divergence”라는 말에만 주목하면 된다는 것인데, 이 divergence의 의미는 벡터장의 발산 같은 개념이 아니라, 그저 “차이”를 다른 말로 쓴 것일 뿐이다는 것을 명심해야 한다.
특히, 여기서 “차이”라고 말하는 것은 두 확률 분포를 비교한다는 말이다.
이 때 정보 엔트로피를 이용해 비교가 진행되다 보니 KL divergence를 또 다른 말로 relative entropy라고 부르기도 한다.
가령, 우리의 목적이 확률 분포 $P$를 정확히 모델링하는 것이라고 하자.
이산확률분포 $P$와 $Q$가 동일한 샘플 공간 $\chi$에서 정의된다고 하면 KL divergence는 다음과 같다.
\[D_{KL}(P\|Q) = \sum_{x\in \chi}P(x)\log_b\left(\frac{P(x)}{Q(x)}\right)\]여기서 로그의 밑 $b$는 2, 10 혹은 $e$ 중 하나로 보통 많이 사용하며, 이 때 각각을 이용했을 때의 정보량 단위는 bit, dit, nit 이다.
식을 조금 더 전개하면,
\[\Rightarrow-\sum_{x\in \chi}P(x)\log_b\left(\frac{Q(x)}{P(x)}\right)\] \[=-\sum_{x\in\chi}P(x)\log_b Q(x) + \sum_{x\in\chi}P(x)\log_b P(x)\]여기서 식 (3)을 잘 보면 두 개의 summation을 포함한 term들은 모두 기댓값으로 치환해 생각해 볼 수 있음을 알 수 있다.
\[\Rightarrow -E_P[\log_bQ(x)]+E_P[\log_bP(x)]\]여기서 기댓값 연산자 $E$에 붙은 subscript ‘P’는 $P(x)$라는 확률분포에 대한 기댓값 연산임을 의미한다.
식 (4)를 조금만 더 전개하면,
\[\Rightarrow H_P(Q) - H(P)\]라고 쓸 수 있는데, $H_P(Q)$는 $P$의 기준으로 봤을 때의 $Q$에 대한 크로스 엔트로피를 의미하고 $H(P)$는 $P$에 대한 정보 엔트로피를 의미한다.
KL-divergence의 시각화.
파란색 함수와 빨간색 함수를 각각 $P(x)$, $Q(x)$라고 했을 때, 초록색 함수에 대한 넓이 합이 KL-divergence 값 $D_{KL}(P\|Q)$을 의미한다.