Prerequisites
이번 포스팅을 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
원의 회전으로 부터 출발하는 정현파
정현파(sinusoidal wave)는 사인파(sine wave), 코사인파(cosine wave)를 총칭하는 말이다.
아마, 중학교 시절 삼각비에 대해서 배우고 고등학교 때 삼각함수에 대해 배운 것을 기억할 것이다.
거기서 삼각함수에 사인파, 코사인파가 포함되어 있다.
지금 생각해보면 고등학교 시절에는 워낙에 어려운 미분/적분을 삼각함수에 적용하고 계산하는 일을 하다보니 막상 정현파의 본질은 잊어버리고 파형의 생김새와 계산 방법만이 머릿속에서 떠돌게 되었던 것 같다.
정현파의 본질은 원 위의 회전에 관한 것이다. 그리고, 시간에 따른 회전을 기술한 것이다.
그림 1. 4초 주기로 원 위의 점이 회전하고 있다.
참고로 회전의 방향은 반시계방향을 기본으로 한다. 처음에 이렇게 정해진 이유는 알 수 없지만, 반시계 방향을 보통 양의 방향으로 본다.
원은 2차원 평면 상에 위치한다. 그런데, 그래프 상에 시간에 따른 회전을 기술(記述)하려다보니 2차원 평면의 두 개 차원 중 하나의 차원은 포기할 수 밖에 없었을 것이다.
가장 쉬운 방법은 회전하는 원의 $x$축 혹은 $y$축 위의 변화만을 시간에 따라 기술하는 것이다.
그림 2. 4초 주기로 원 위의 점의 x 축 y 축 위의 변화만을 관찰하는 과정
위 그림에서 볼 수 있는 시간에 따른 $x$ 축 혹은 $y$ 축 위의 움직임을 아래와 같이 표현하는 것이 아이디어라고 할 수 있다. 시간 축을 새로 설정하자는 것이다.
그림 3. 원 위의 회전에 맞춰 x 축 y 축의 시간 변화를 각각 그래프로 표현하면 정현파를 얻을 수 있다.
이렇게 해서 얻게 되는 파형은 두 개이고 $x$ 축의 시간 변화 그래프는 코사인 파라고 부르고 $y$ 축의 시간 변화 그래프는 사인파라고 부른다.
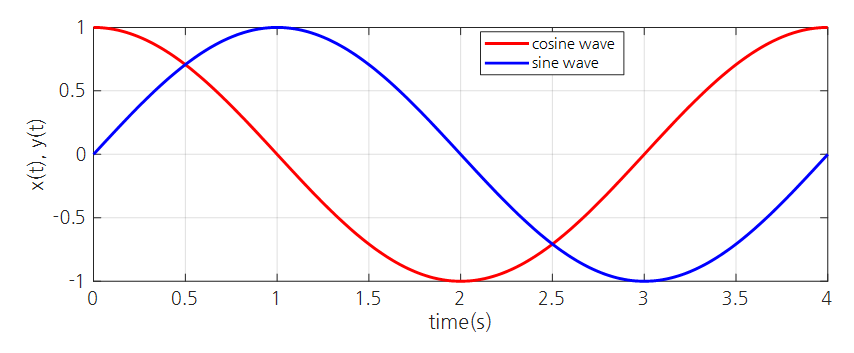
그림 4. 주기가 4초인 코사인파와 사인파
정현파의 3가지 특성값
우리는 앞서 원의 회전으로부터 정현파를 생각할 수 있다는 것을 알아보았다.
이 사실을 기반으로 원의 회전에 관한 몇 가지 변형을 줄 수 있다는 것을 상상해볼 수 있다.
일단 원의 반지름을 수정해볼 수 있을 것이고, 또 회전 속도를 조절 해볼 수도 있을 것이다.
거기에, 회전하기 시작하는 곳의 위치도 바꿔볼 수 있다.
이 세 가지는 각각 정현파의 진폭(amplitude), 주파수(frequency), 위상 변이(phase shift)라고 불린다.
코사인파를 기준으로 쓰면 다음과 같이 진폭, 주파수, 위상 변이가 표현된다.
\[x(t)=A\cos(2\pi f_0 t+\phi) = A\cos(\omega_0 t + \phi)\]여기서 $A$는 진폭, $f_0$는 주파수, $\phi$는 위상 변위를 뜻하며 $\omega_0$는 라디안 주파수를 의미한다.
이것에 대해서 조금 더 자세히 알아보도록 하자.
진폭 (amplitude)
진폭은 크게 어려운 개념이 아니다. 정현파의 진폭은 회전하는 원의 반지름의 길이와 같다.
그림 5. 서로 다른 크기의 반지름을 갖는 원의 회전
기본적으로 코사인 함수 $cos(\theta)$는 +1과 -1 사이에서 진동하므로 $A\cos(\theta)$는 $-A$에서 $+A$ 사이에서 진동한다.
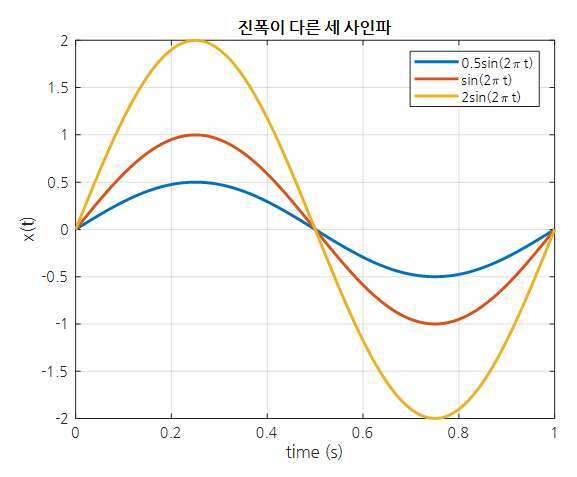
그림 6. 서로 다른 진폭을 가지는 세 개의 사인파
다만, 정현파를 그릴 때, 가로축을 시간, 세로축을 amplitude라고 많이들 적는데, 그것은 올바른 표현은 아니라는 점은 짚고 넘어갔으면 좋을 것 같다.
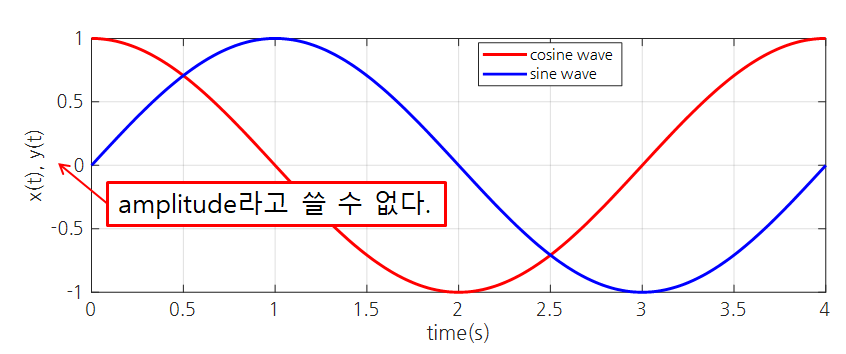
그림 7. 세로축의 label을 amplitude라고 쓰는 것은 잘못 표기하는 것이다.
주파수 (frequency)
주파수의 개념은 회전 속도와 관련되어 있다. 얼마나 빨리 회전하는지에 관한 것이다.
빨리 회전할 수록 주파수는 높다.
그림 8. 서로 다른 크기의 주파수를 갖는 원의 회전
주파수는 주기의 역수인데, 1/s 단위를 Hz(헤르츠)라고 읽는다.
따라서, 0.25 Hz는 4초에 한번 회전, 1 Hz는 1초에 한번 회전, 2 Hz는 0.5초에 한번 회전하는 경우를 의미한다.
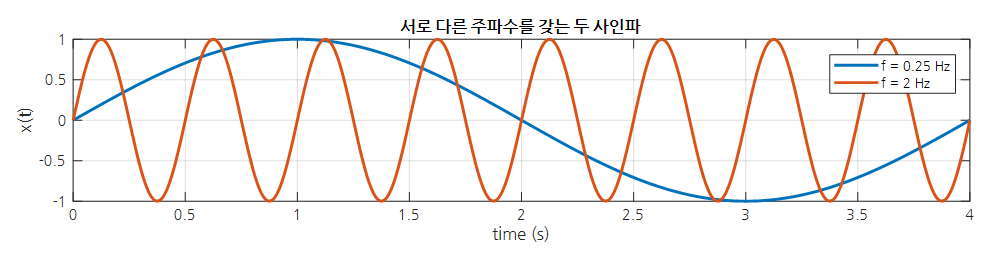
그림 9. 0.25 Hz와 2Hz의 서로 다른 주파수를 갖는 사인파의 형태 비교
정현파의 주파수와 관련해 어렵게 여기는 개념중 하나는 라디안 주파수이다. 라디안 주파수는 보통 $\omega$(오메가 라고 읽는다.)를 기호로 사용한다.
라디안 각도 체계은 원을 한번 회전할 때 반지름과 회전한 길이의 비율이 항상 $2\pi$임을 고려해 만든 각도 체계이다.
1Hz가 1초에 한번 회전하는 것을 의미한다고 하면 라디안 주파수는 1초에 몇 라디안을 회전하는지를 쉽게 파악하려고 만든 개념이다.
가령 $2\pi$ rad/s의 라디안 주파수는 1초에 1번 도는 회전을 의미한다. 다만, 라디안 각도 체계를 이용해 얼마나 회전했는지에 대해 표현한 것이다.
그래서 Hz를 이용해 표기하는 주파수를 $f$라고 쓰고 라디안 주파수를 $\omega$라고 쓰면,
\[\omega = 2\pi f\]와 같은 관계를 갖는다.
위상 변이(phase shift)
정현파를 공부할 때 위상에 대한 내용을 어려워 하는 경우가 많다.
위상이라는 말은 지구과학에서 달(Moon)에 대해 공부할 때나 나오는 말이라 생소하기 때문이기도 하다.
phase shift가 되면 아래 그림과 같이 정현파가 좌/우로 옮겨지게 된다.
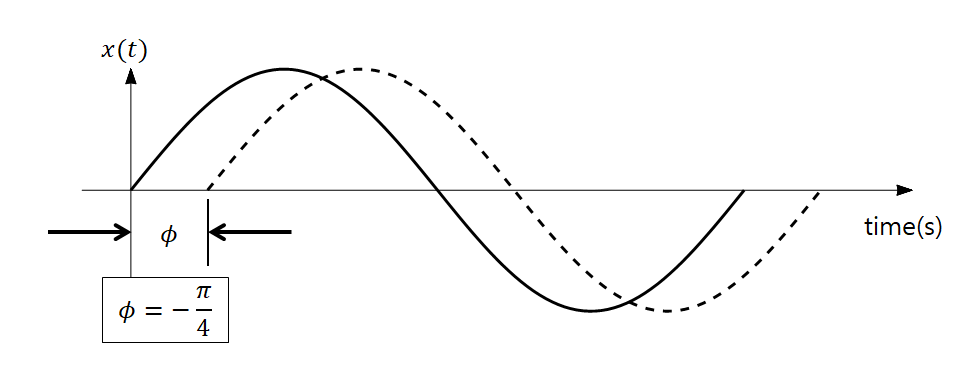
그림 10. phase shift가 일어나면 정현파가 좌/우로 움직이게 된다.
좌/우로 움직이는 현상에 대해 헷갈린다면 정현파의 고향인 원의 회전을 다시 생각해보자.
다시 말해, 위상은 ‘원의 어디서부터 출발할 것인가?’를 말해주는 것이다.
즉, 식 (1)에서 $\phi$ 는 회전을 시작하는 위치에 불과하다.
그림 11. 서로 다른 위상 변위를 갖는 원의 회전에 대한 sine 파 도시
그래서 phase를 shift해줬다는 것을 고려할 때는 어디서부터 회전을 시작할 것인가를 생각하면 충분한 것이다.
다만 조금 헷갈리기 쉬운 부분은 phase shift에 의한 time delay인데, 쉽게 생각하려면 식 (1)을 다음과 같이 변형하면 된다.
\[\text{식 (1)} \Rightarrow A\cos\left(2\pi f\left(t+\frac{\phi}{2\pi f}\right)\right)=A\cos\left(2\pi f\left(t-t_d\right)\right)\]즉, $\phi$ 라디안 만큼 phase shift가 있었다고 하면, 이에 의해 발생하는 time delay $t_d$는
\[t_d = -\frac{\phi}{2\pi f}\]초라고 할 수 있다.