L’Hopital’s Rule

There is a famous theorem known as L’Hopital’s Rule, which was often referred to as a “trick” when studying limits in high school.

Usually, in high school, it is simply mentioned without rigorous proof, as proving it requires mathematical knowledge beyond high school level. So, in most cases, the proof is omitted.

We roughly know L’Hopital’s Rule as the following equation (1):

\[\lim_{t\rightarrow \alpha}\frac{f(t)}{g(t)} = \lim_{t\rightarrow \alpha}\frac{f'(t)}{g'(t)}\]

Even with this rough understanding, we can easily calculate limits like the following:

\[\lim_{x\rightarrow 0}\frac{\sin x}{x} = \lim_{x\rightarrow 0}\frac{(\sin x)'}{(x)'} = \lim_{x\rightarrow 0}\frac{\cos x}{1} = 1\]

In fact, L’Hopital’s Rule does not deviate much from equation (1), but it is defined with some additional conditions, and these conditions must be carefully considered when using L’Hopital’s Rule to calculate limits.

DEFINITION 1. L’Hopital’s Rule

Let $f(t)$ and $g(t)$ be real-valued functions1, and $\alpha$ be one of the following limit values. $$\alpha^{\pm}, \alpha^+, \alpha^-, +\infty, -\infty \notag$$ Also, let $L$ be a real number or $+\infty$ or $-\infty$. Then, if $$\lim_{t\rightarrow \alpha}\frac{f'(t)}{g'(t)}=L$$ and $(i) \lim_{t\rightarrow \alpha}g(t) = \lim_{t\rightarrow \alpha}f(t) = \pm\infty$ or $(ii) \lim_{t\rightarrow \alpha}g(t) = \lim_{t\rightarrow \alpha}f(t) = 0$ $$\lim_{t\rightarrow \alpha}\frac{f(t)}{g(t)} = L$$ holds.

One important point to note from DEFINITION 1 is that, although many people think of using L’Hopital’s Rule by differentiating the numerator and denominator to find the limit of $f(t)/g(t)$, originally, L’Hopital’s Rule states that the limits of $f(t)/g(t)$ and $f’(t)/g’(t)$ are equal only when the limit of $f’(t)/g’(t)$ exists.

Also, it is worth noting that L’Hopital’s Rule can only be used when both the numerator and denominator of the limit we want to calculate converge to 0 (i.e., in the form of 0/0) or diverge to infinity (i.e., in the form of $\infty/\infty$).

Geometrical Understanding of L’Hopital’s Rule

To understand L’Hopital’s Rule geometrically, let’s consider the parametric equations as follows and think of $g(t)$ and $f(t)$ as points on a plane, as shown in equation (5) and Figure 1.

\[(x, y) = (g(t), f(t))\]

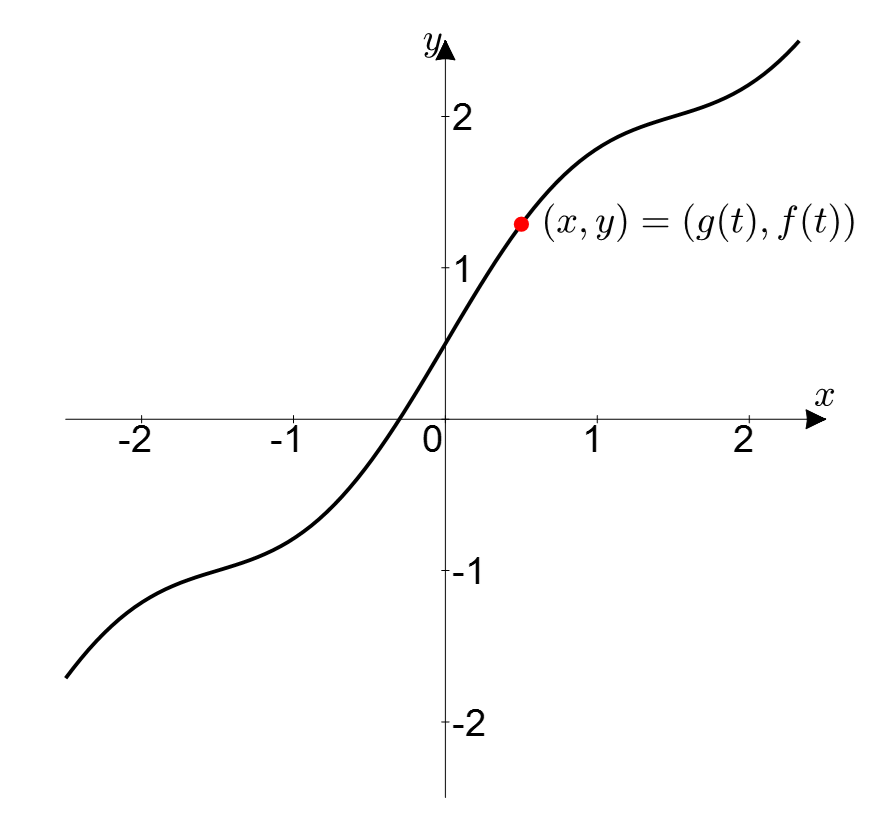
Figure 1. Consider $g(t)$ and $f(t)$ as points on a plane with $t$ as a parameter.

By doing this, we can replace the two functions with a single curve.

Furthermore, we can think of it in the following way:

\[\frac{f'(t)}{g'(t)} = \frac{dy/dt}{dx/dt} = \frac{dy}{dx}\] \[\frac{f(t)}{g(t)} = \frac{y}{x}\]

In other words, what equation (6) means is the instantaneous rate of change of $(x, y)$ along the path shown in Figure 1, and equation (7) represents the average rate of change from the origin to $(x, y)$.

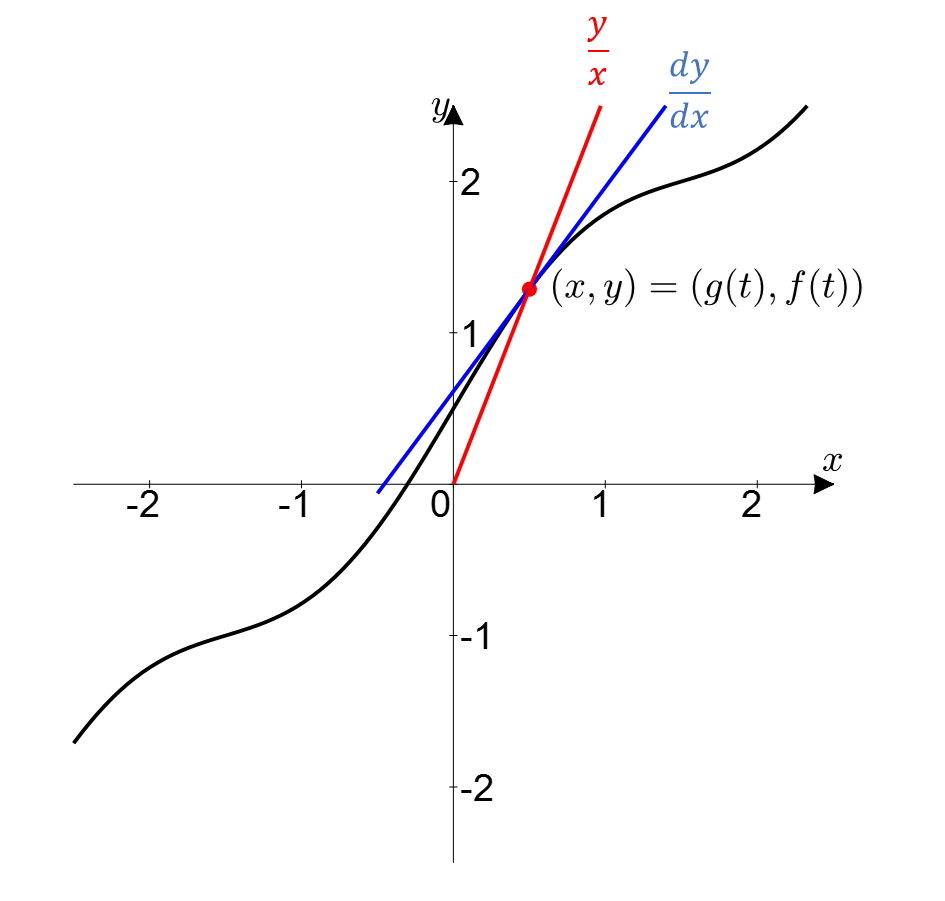
Figure 2. The meaning of $f'(t)/g'(t)$ and $f(t)/g(t)$ on the parametric curve in terms of instantaneous rate of change (blue) and average rate of change (red).

Now, L’Hopital’s Rule is about limits, specifically approaching $t$ towards some $\alpha$. Taking a limit with respect to $\alpha$ in Figure 1 or 2 can be interpreted as approaching a point $(x, y)$ somewhere on the curve.

In doing so, we can observe how the instantaneous rate of change and average rate of change change as $t$ approaches $\alpha$.

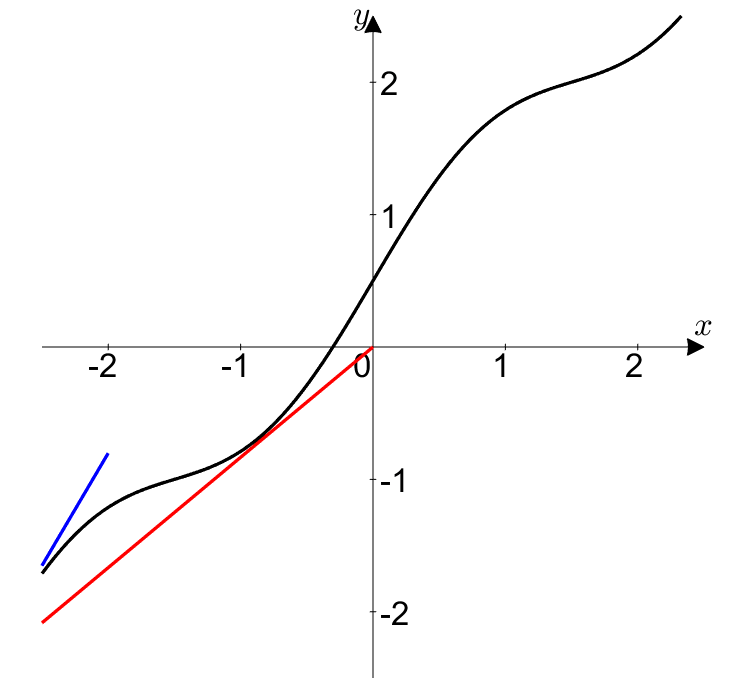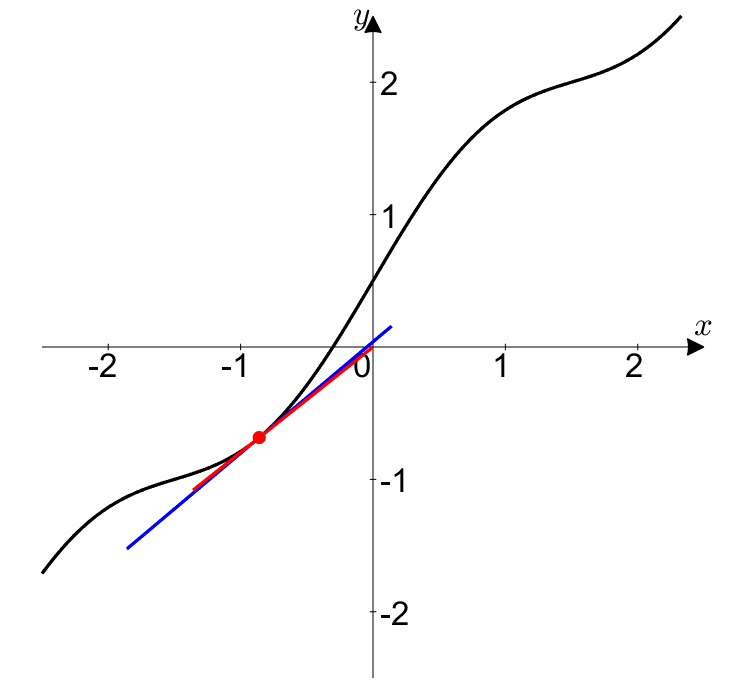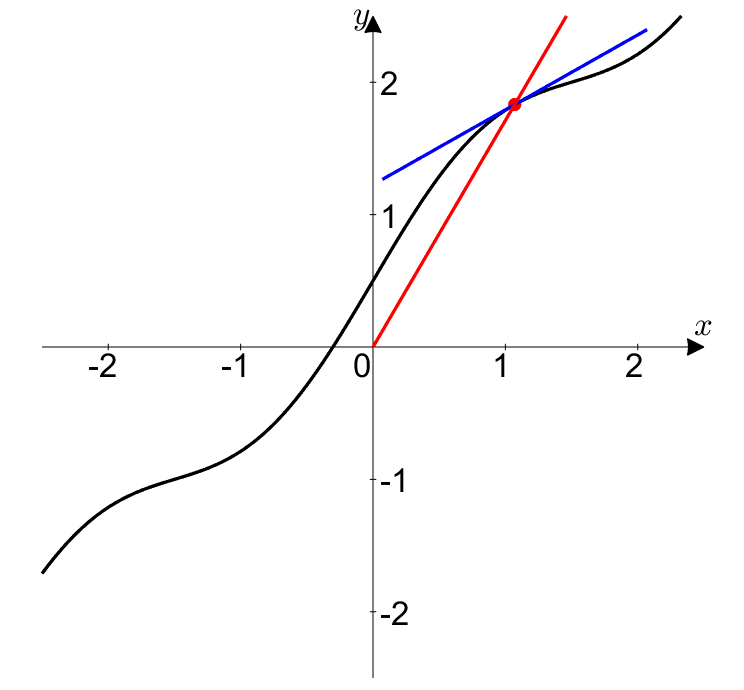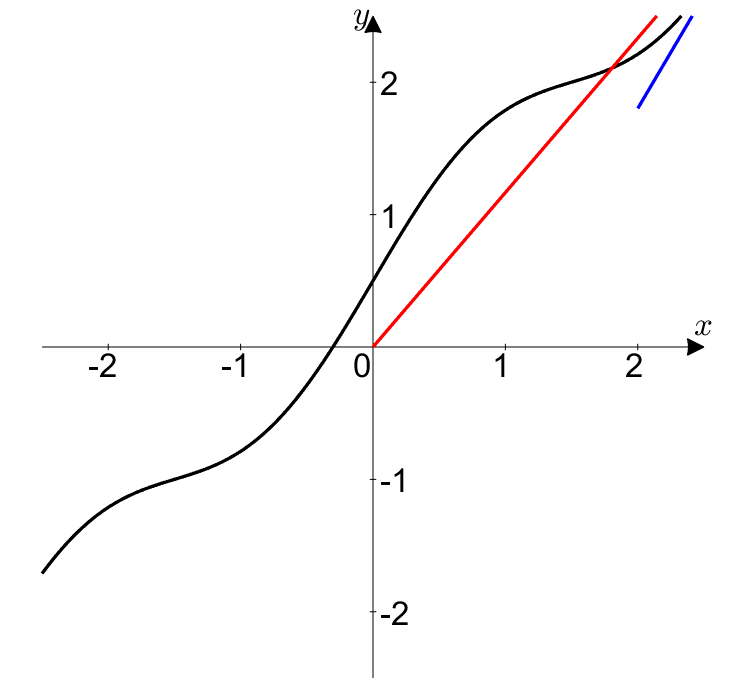
Figure 3. Approaching the red dot to a point $(x, y)$ on the curve by letting $t \rightarrow \alpha$ is equivalent to saying that the instantaneous rate of change (blue) and average rate of change (red) change accordingly.

So, which point on the curve should we approach the red dot to?

In the case of 0/0 form:

If we revisit the definition of L’Hopital’s rule discussed in DEFINITION 1, we can see that L’Hopital’s rule applies only to expressions that are in the form of 0/0 or $\infty / \infty$. Let’s first understand the case when the expression is in the form of 0/0.

0/0 means that as $t$ approaches $\alpha$, both $f(t)$ and $g(t)$ converge to 0.

In other words, as shown in Figure 4 below, the curve defined by $(x,y)=(g(t), f(t))$ should approach 0 as the limit of $x=g(t)$ approaches 0, and also as the limit of $y=f(t)$ approaches 0.

In simpler terms, the curve should pass through the point (0,0). (More rigorously, it is not necessary for the curve to pass through the point (0,0), but it is sufficient for the limit of both $f(t)$ and $g(t)$ to be 0.)

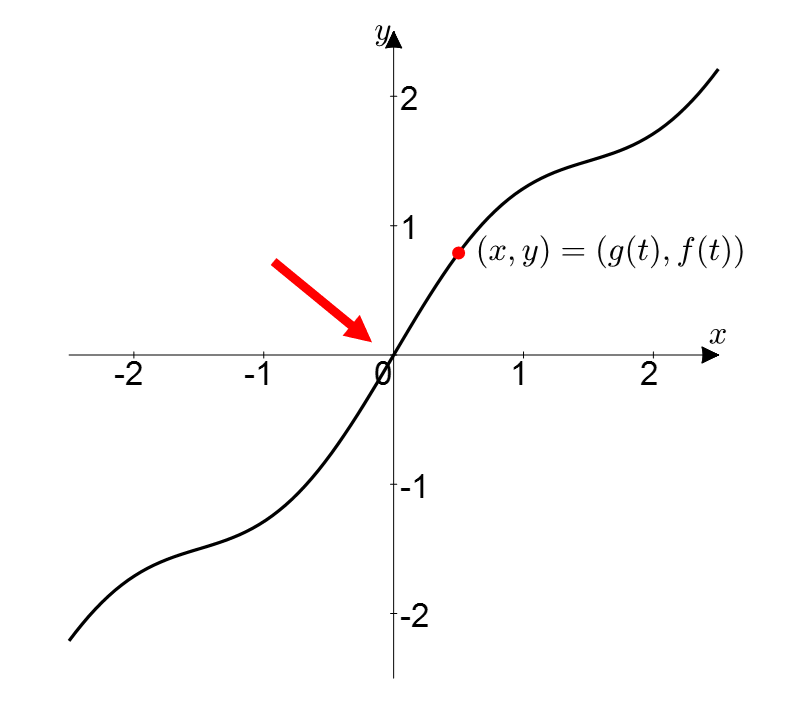
Figure 4. The shape of the curve to understand L'Hopital's rule in the case of 0/0 form

Let’s assume that as $t$ approaches $\alpha$, the limit of $f’(t)/g’(t)$ (i.e., the instantaneous slope) converges to $L$.

Then, will the value of $f(t)/g(t)$ (i.e., the average slope) be the same?

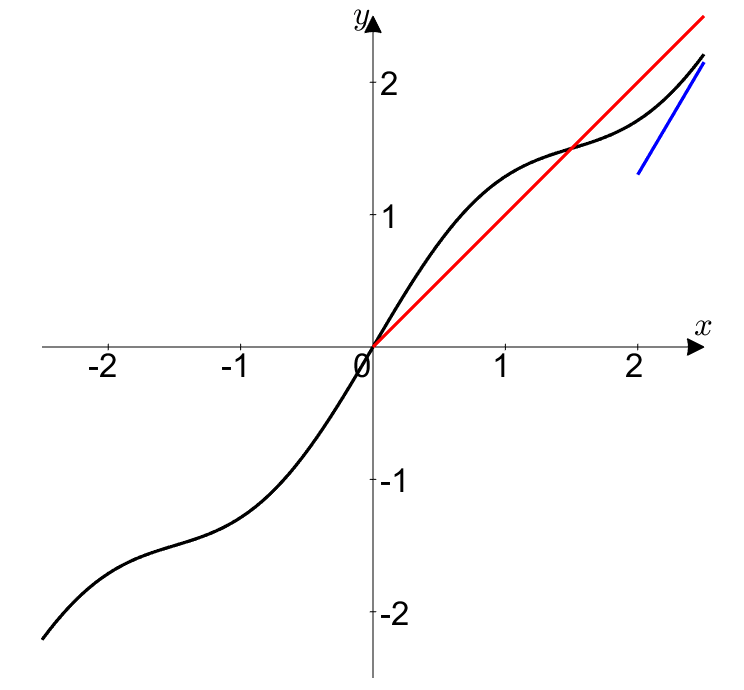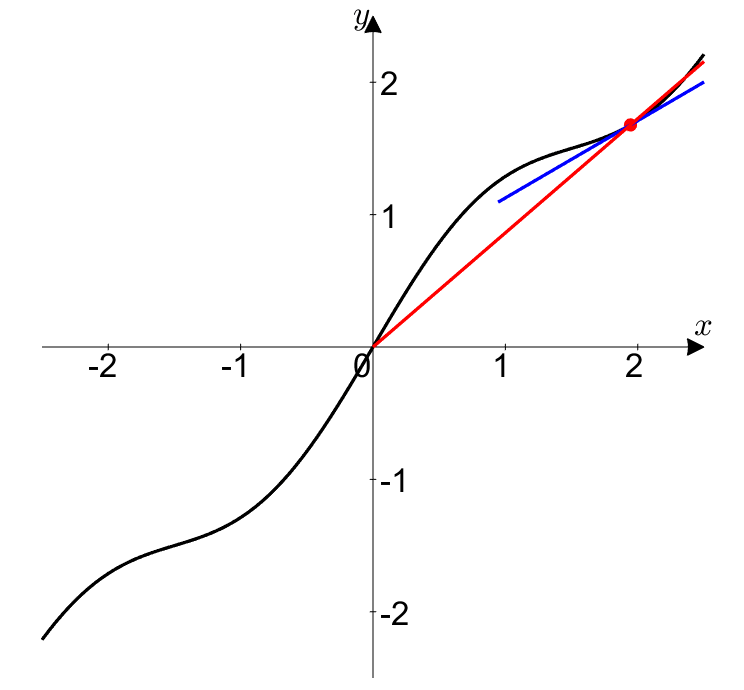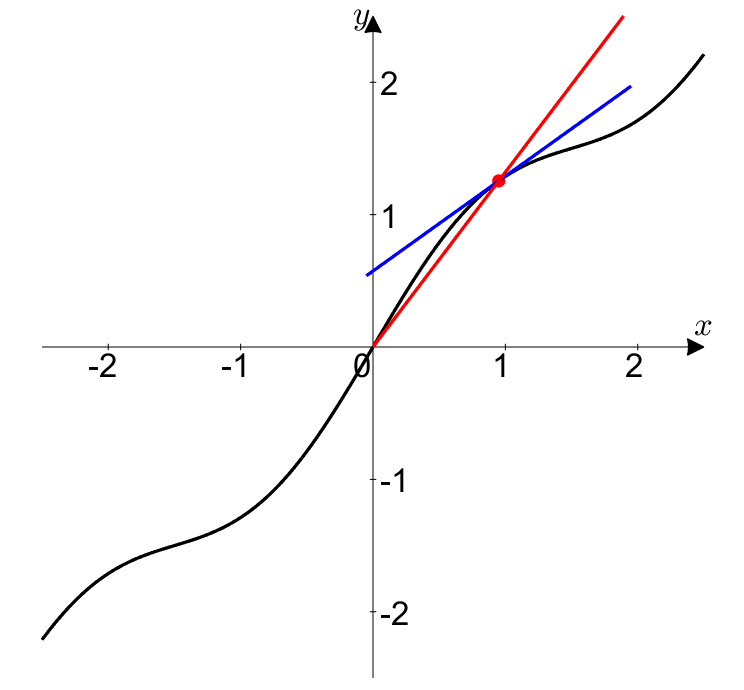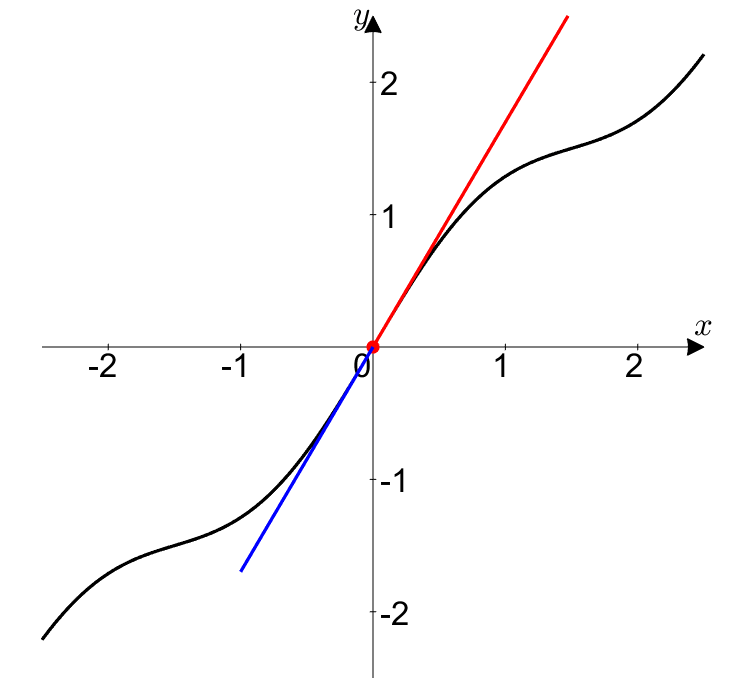
Figure 5. When both $f(t)$ and $g(t)$ approach 0 in the case of 0/0 form, the instantaneous slope and the average slope become the same.

In other words, L’Hopital’s rule for 0/0 form is telling us the following:

If the instantaneous slope at (0,0) is $L$, then as $(x,y)$ approaches (0,0), the average slope approaches $L$ very closely.

In the case of $\infty / \infty$ form:

If the expression is in the form of $\infty / \infty$, we can assume a curve that has a slope equal to the given value of $L$ as $x = g(t)$ and $y = f(t)$ both tend to infinity.

Figure 6. Creating a curve that maintains the instantaneous slope as $L$ while both $f(t)$ and $g(t)$ tend to $\infty$, and taking the limit as $t$ approaches $\infty$ to make the instantaneous slope and average slope the same.

In other words, the l’Hopital’s rule for $\infty / \infty$ form is telling us the following:

If the instantaneous slope at $(\infty,\infty)$ is $L$, then as $(x,y)$ approaches $\infty$, the average slope approaches $L$ very closely.

Reference:

• Paths and geometry of l’Hopital’s Rule, Frank J. Swenton