Prerequisites
해당 post를 잘 이해하기 위해서는 다음의 내용에 대해 알고 오시는 것을 추천드립니다.
벡터의 불변성과 가변성
벡터의 기본 연산에서는 벡터가 무엇인가에 대해 다룰 때 벡터란 “화살표 같은 것”이면서 동시에 “숫자를 순서대로 나열한 것”이라는 두 가지의 특징에 대해 설명한 바 있다.
아래의 그림은 이러한 벡터의 불변성과 가변성을 한번에 설명해주고 있는 그림으로, 좌표계가 변하더라도 빨간색으로 표시한 화살표는 요지부동(불변성)이다. 하지만, 동시에 다른 좌표계를 통해 본 벡터의 좌표는 (3, 4)에서 (3.6, 3.4)로 바뀐 것(가변성)을 볼 수 있다.
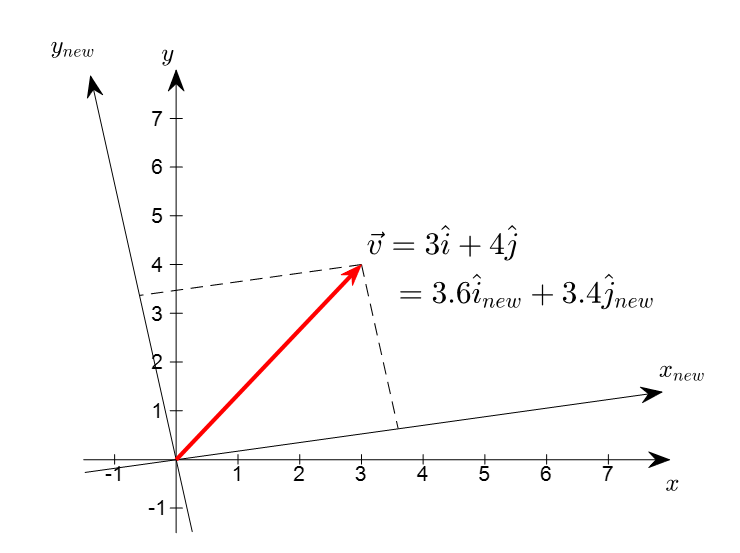
그림 1. 좌표계의 변환과 벡터. 좌표계가 변할 때 벡터는 변하지 않지만 벡터의 성분은 변한다.
이번 post에서는 벡터를 표현하는 좌표계를 변경시켰을 때, 어떻게 기존의 벡터를 새롭게 표현할 수 있는지에 대해 알아보고자 한다.
새로운 좌표계 = 새로운 기저의 도입
표준 기저를 이용한 좌표 표현
좌표평면 상의 어떤 점(즉 벡터)을 표현할 때 우리가 보통 사용하는 좌표계는 cartesian coordinate이다.
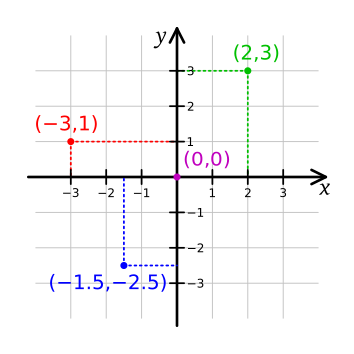
그림 2. 데카르트 좌표계의 2차원 실수 공간 상의 좌표 평면
그림 출처: 위키피디아, 데카르트 좌표계
일반적인 데카르트 좌표계에서 이용되는 기저 벡터는 $(1,0)$과 $(0,1)$을 가르키는 벡터를 이용하고, 각각을
\[\hat{i} = \begin{bmatrix}1 \\0 \end{bmatrix}\]과
\[\hat{j} = \begin{bmatrix}0\\1\end{bmatrix}\]로 쓴다.
다시 말해, 기저 벡터란 해당 좌표계를 구성하는 가로 세로 눈금 한 칸을 얼마만큼의 길이로 정할것인지를 정해주는 것이라고 생각할 수 있다.
또한 데카르트 좌표계 상의 임의의 점, 가령 (2,3)이라는 점은 두 기저 벡터의 선형결합으로 표현할 수 있는데, 다시 말해
\[\begin{bmatrix}2\\3 \end{bmatrix} = 2\begin{bmatrix}1\\0 \end{bmatrix} + 3\begin{bmatrix}0\\1 \end{bmatrix} = 2\hat{i} + 3\hat{j}\]라고 쓸 수 있다는 점이다.
여기서 우리는 용어를 하나 정의하고자 하는데, 앞으로는 데카르트의 좌표계의 기저벡터들($\hat{i}, \hat{j}$)을 표준 기저(standard basis)라고 부르도록 하자.
신규 기저를 이용한 좌표 표현
만약 표준 기저가 아닌 전혀 새로운 기저를 이용해 좌표계를 구성한다고 하면 임의의 벡터를 어떻게 다시 표현할 수 있을까?
아래와 같은 새로운 기저 벡터들의 집합을 생각해보자.
\[\mathcal{B} = \left\lbrace \vec{b_1}, \vec{b_2} \right\rbrace = \left\lbrace\begin{bmatrix}1 \\ 1\end{bmatrix}, \begin{bmatrix}-1 \\ 1\end{bmatrix}\right\rbrace\]
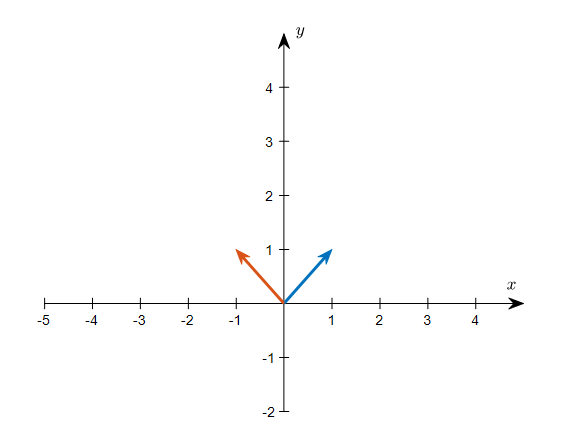
그림 3. 임의의 새로운 기저 벡터 집합 $\mathcal{B}$의 두 기저 벡터
기저 집합 $\mathcal{B}$를 이용하여 새로운 좌표계를 생각하고, 임의의 벡터를 새로운 기저를 이용해 표현해보자.
가령, 표준 기저를 이용해 표현한 벡터 (2, 2)를 놓고 생각해보자.
원래의 데카르트 좌표계와 새로운 좌표계를 동시에 놓고 생각해본다면 다음의 그림 4와 같을 것이다.
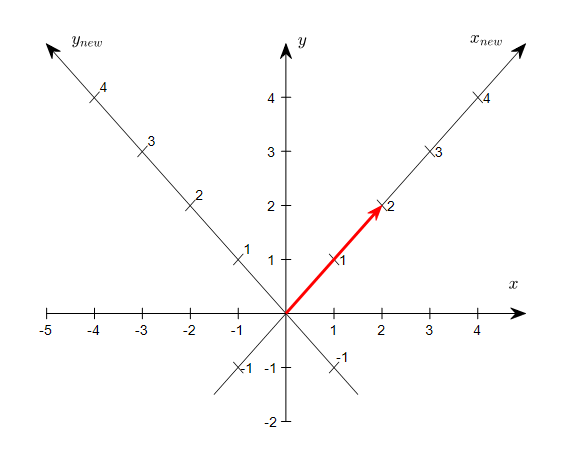
그림 4. 표준 기저로 표현한 벡터 (2,2)에 대한 원래 좌표계와 새로운 좌표계에서의 관찰
그림 4에서 볼 수 있듯이 표준 기저에서는 (2, 2)로 표현되던 좌표 (빨간색 화살표)가 새로운 좌표게에서는 (2, 0)으로 표현하면 충분할 것으로 보인다.
앞으로 기저가 변경되는 경우 벡터를 표현할 때 아랫첨자로 기저가 되는 벡터 집합의 이름을 기재하도록 하자.
가령, 표준 기저에서 표현되는 (2,2) 벡터는
\[\begin{bmatrix}2\\ 2\end{bmatrix}_{\mathcal{E}}\]라고 표현하고, 새로운 기저 $\mathcal{B}$를 기반으로 하여 표현되는 벡터 (1, 0)은
\[\begin{bmatrix}2\\ 0\end{bmatrix}_{\mathcal{B}}\]라고 쓰자.
그렇다면, 그림 4에서 보았던 것 처럼 아래의 두 벡터 표현은 동일한 벡터에 대한 다른 표현임을 알 수 있다.
\[\begin{bmatrix}2\\ 2\end{bmatrix}_{\mathcal{E}}, \begin{bmatrix}2\\ 0\end{bmatrix}_{\mathcal{B}}\]즉, 위 식은 다음과 같이 해석할 수 있다.
$\Rightarrow \mathcal{B}$라는 기저를 가지고 만든 좌표계에서의 (2, 0)은 표준 좌표계에서는 (2, 2)로 쓸 수 있다.
그런데, 식 (6)에서의 기저 $\mathcal{B}$를 이용해 표현한 (2,0)라는 좌표값은 어떻게 얻을 수 있었을까?
원래의 표준 좌표계에서의 좌표 $(2,2)$를 $\mathcal{B}$의 기저들을 이용해 표현한다고 하고, 기저 $\mathcal{B}$를 이용해 표현한 좌표는 $(k_1, k_2)$라고 하자.
즉 표준좌표계에서의 좌표 (2,2)와 새로운 기저를 이용해 표현한 좌표 $(k_1, k_2)$는 아래와 같은 관계식을 만족해야 한다.
\[\begin{bmatrix}2\\2\end{bmatrix}=k_1\begin{bmatrix}| \\ b_1 \\ |\end{bmatrix}+k_2\begin{bmatrix}| \\ b_2 \\ |\end{bmatrix}\]위 식을 보면 바로 떠오를 수 있는 것은 행렬 곱에 대한 또 다른 시각편에서 보았던 것 처럼 위 식의 우변은 행렬과 벡터의 곱의 해석 중 ‘열벡터의 선형 결합’을 이용해 아래와 같이 다시 쓸 수 있다는 것이다.
\[\begin{bmatrix}2\\2\end{bmatrix} = \begin{bmatrix}| & | \\ b_1 & b_2 \\ | & |\end{bmatrix}\begin{bmatrix}k_1\\k_2\end{bmatrix}\]우리에게 주어진 $\mathcal{B}$의 기저는 아래와 같으므로,
\[\mathcal{B} = \left\lbrace\begin{bmatrix}1 \\ 1\end{bmatrix}, \begin{bmatrix}-1 \\ 1\end{bmatrix}\right\rbrace\] \[\begin{bmatrix}2\\2\end{bmatrix} = \begin{bmatrix}1 & -1 \\1 & 1\end{bmatrix}\begin{bmatrix}k_1\\k_2\end{bmatrix}\]를 만족하는 $k_1$과 $k_2$를 구하면 (2,0)이라는 답을 얻을 수 있는 것이다.
\[\therefore \begin{bmatrix}k_1\\k_2\end{bmatrix}=\begin{bmatrix}1 & -1 \\ 1 & 1\end{bmatrix}^{-1}\begin{bmatrix}2\\2\end{bmatrix} = \begin{bmatrix}2\\0\end{bmatrix}\]이 결과를 일반화해보면, 표준좌표계의 임의의 벡터에 대해서 임의의 기저 $\mathcal{C}$로 구성된 좌표계의 좌표는 다음과 같이 얻을 수 있다.
표준 좌표계에서의 임의의 벡터를 $x$라고 하자.
\[x=\begin{bmatrix}x_1 \\ x_2\end{bmatrix}_{\mathcal{E}}\]그리고 기저 $\mathcal{C}$를 다음과 같이 생각하자.
\[\mathcal{C}=\left\lbrace\begin{bmatrix}| \\ c_1 \\ |\end{bmatrix}, \begin{bmatrix} | \\ c_2 \\ | \end{bmatrix}\right\rbrace\]그리고 벡터 $x$에 대해서 기저 $\mathcal{C}$로 구성된 좌표계에서의 좌표를 다음과 같이 생각하자.
\[y=\begin{bmatrix}y_1\\y_2\end{bmatrix}_{\mathcal{C}}\]그렇다면 다음과 같은 관계를 생각할 수 있다.
\[\begin{bmatrix}x_1\\x_2\end{bmatrix}_{\mathcal{E}} = \begin{bmatrix}| & | \\ c_1 & c_2 \\ | & |\end{bmatrix}\begin{bmatrix}y_1\\y_2\end{bmatrix}_{\mathcal{C}}\]임의의 기저 간의 변환
2차원 실수 공간 $\Bbb{R}^2$의 두 개의 기저 $\mathcal{B}=\lbrace v_1, v_2\rbrace$와 $\mathcal{C}=\lbrace w_1, w_2\rbrace$를 생각해보자.
$\Bbb{R}^2$의 모든 벡터들은 $v_1$과 $v_2$에 대한 일차결합으로 표현할 수 있으므로 다음과 같이 나타낼 수 있다.
\[w_1 = a v_1 + b v_2\] \[w_2 = c v_1 + d v_2\]
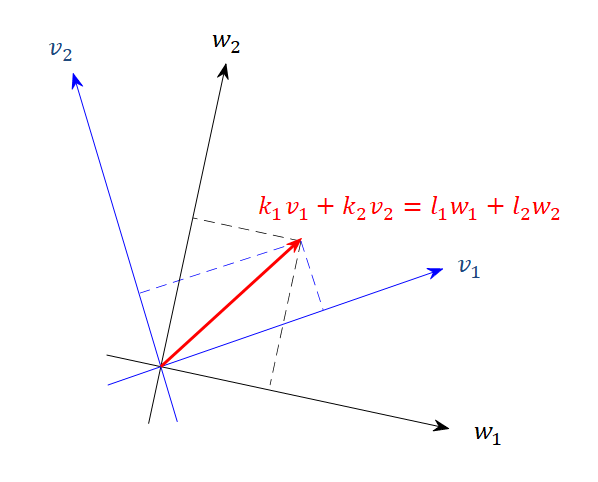
그림 5.
그림 5에서 벡터 $v=l_1 w_1 + l_2 w_2$를 $v_1$과 $v_2$로 나타내면,
\[v = l_1 w_1 + l_2 w_2\] \[=l_1(a v_1 + b v_2) + l_2 (cv_1 +dv_2)\] \[=(a l_1 + cl_2)v_1 + (bl_1 + d l_2)v_2\] \[=k_1v_1 + k_2v_2\]이므로, 좌표 벡터와 행렬을 이용하면
\[[v]_{\mathcal{B}} = \begin{bmatrix}k_1 \\ k_2\end{bmatrix} = \begin{bmatrix}al_1 + cl_2 \\ bl_1 + dl_2\end{bmatrix} = \begin{bmatrix}a & c \\ b & d\end{bmatrix}\begin{bmatrix}l_1 \\ l_2\end{bmatrix}=\begin{bmatrix}a & c \\ b & d\end{bmatrix}[v]_{\mathcal{C}}\]이라 할 수 있다.
이 때 벡터 $v$의 $\mathcal{C}$ 표현
\[[v]_{\mathcal{C}}\]를 $\mathcal{B}$ 표현
\[[v]_{\mathcal{B}}\]로 바꾸어주는 행렬
\[\begin{bmatrix}a & c \\ b & d\end{bmatrix}\]을 기저변환행렬(transition matrix) 혹은 추이행렬이라고 한다.