로피탈 정리만 생각하면 아직도 그분의 외침이 들린다. 아니 선생!...

로피탈 정리

고교 시절 극한을 공부할 때 일명 ‘꼼수’로 통했던 정리가 하나 있으니, 로피탈의 정리이다.

보통은 고등학교 시절에는 간단히 언급이 되기만 하거나, 엄밀한 증명을 위해선 고등학교 수준을 넘는 수학지식이 필요하므로 증명이 생략되는 경우가 거의 대부분이다.

로피탈의 정리를 우리가 대충 알고 있기로는 아래의 식 (1)과 같은데,

\[\lim_{t\rightarrow \alpha}\frac{f(t)}{g(t)} = \lim_{t\rightarrow \alpha}\frac{f'(t)}{g'(t)}\]

이런 대략적인 내용만 알고있어도 아래와 같은 극한을 쉽게 구할 수 있다.

\[\lim_{x\rightarrow 0}\frac{\sin x}{x} = \lim_{x\rightarrow 0}\frac{(\sin x)'}{(x)'} = \lim_{x\rightarrow 0}\frac{\cos x}{1} = 1\]

사실 로피탈의 정리는 식 (1)에서 크게 벗어나지 않는데, 몇 가지 조건을 추가해서 정의되며 로피탈의 정리를 이용해 극한을 계산할 때에는 이러한 조건들을 꼼꼼히 고려해야한다.

DEFINITION 1. 로피탈의 정리

실수함수 $f(t)$와 $g(t)$에 대하여1, $\alpha$는 다음 중 하나의 극한값을 갖는다고 하자. $$\alpha^{\pm}, \alpha^+, \alpha^-, +\infty, -\infty \notag$$ 또, $L$은 실수이거나 $+\infty$ 혹은 $-\infty$로 발산한다고 하자. 이 때, 만약 $$\lim_{t\rightarrow \alpha}\frac{f'(t)}{g'(t)}=L$$ 이고, $\text{(i) }\lim_{t\rightarrow \alpha}g(t) = \lim_{t\rightarrow \alpha}f(t) = \pm\infty$ 또는 $\text{(ii) }\lim_{t\rightarrow \alpha}g(t) = \lim_{t\rightarrow \alpha}f(t) = 0$ 이라면 $$\lim_{t\rightarrow \alpha}\frac{f(t)}{g(t)} = L$$ 이다.

DEFINITION 1에서 주목해야할 점 중 하나는, 보통 많이들 알고 있기로는 $f(t)/g(t)$의 극한을 풀기 위해 분자, 분모를 미분해서 극한값을 구하는 방식으로 로피탈의 정리를 이용한다고 생각하지만,

원래는 로피탈의 정리는 $f’(t)/g’(t)$의 극한이 존재하는 경우에야 $f(t)/g(t)$의 극한과 $f’(t)/g’(t)$의 극한이 같다는 것을 말해주고 있다는 점이다.

또, 구하고자 하는 $f(t)/g(t)$의 극한에 대해서, 분자, 분모가 모두 0 으로 수렴하거나(즉, 0/0 꼴) 무한대로 발산할 때(즉, $\infty/\infty$ 꼴)에야 비로소 로피탈의 정리가 사용될 수 있다는 점 역시 주목해야할 점이다.

로피탈 정리의 기하학적 이해

로피탈의 정리를 기하학적으로 이해하기 위해 다음과 같이 매개변수 방정식을 이용해 아래의 식 (5) 및 그림 1과 같이 $g(t)$와 $f(t)$를 평면상의 경로의 한 점으로 생각하자.

\[(x, y) = (g(t), f(t))\]

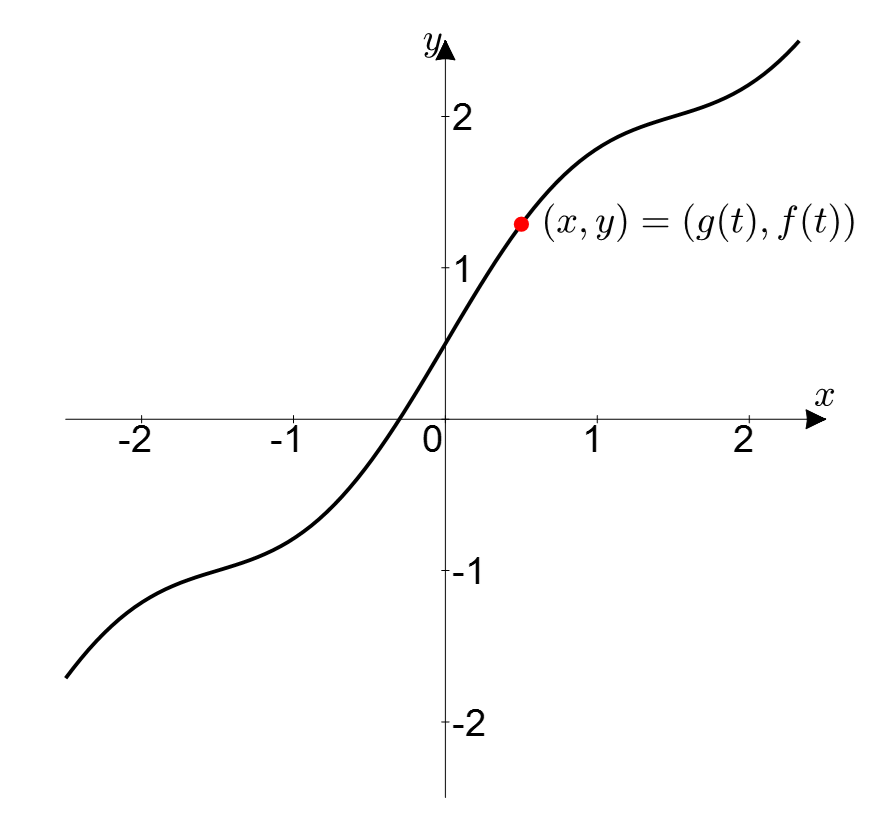
그림 1. $t$를 매개변수로 하여 함수 $g(t), f(t)$를 평면상의 한 점으로 생각하자.

이런 처리를 해줌으로써 두 개의 함수를 하나의 곡선으로 대체해 생각할 수 있다.

또, 다음과 같이 바꿔 생각할 수 있다.

\[\frac{f'(t)}{g'(t)} = \frac{dy/dt}{dx/dt} = \frac{dy}{dx}\] \[\frac{f(t)}{g(t)} = \frac{y}{x}\]

즉, 식 (6)이 의미하는 것은 그림 1의 경로에서 $(x, y)$의 순간 변화율을 의미하고, 식 (7)은 원점에서부터 $(x, y)$까지의 평균 변화율을 의미하게 된다.

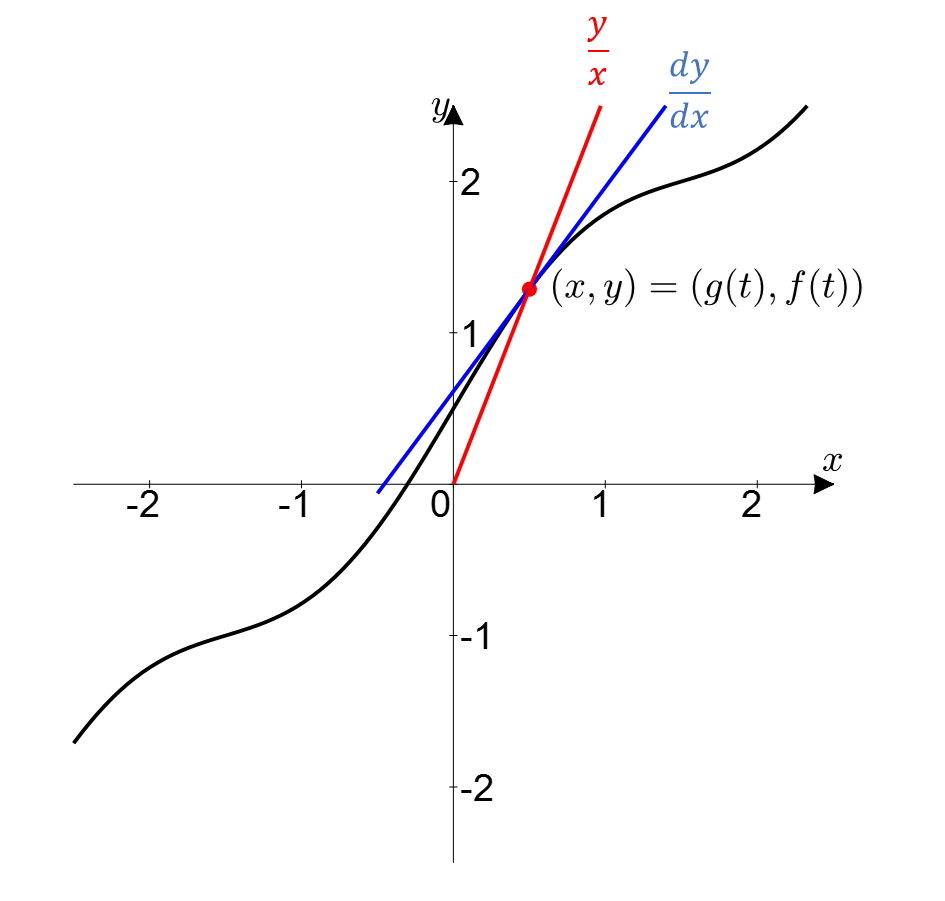
그림 2. 매개변수를 이용한 곡선에서 $f'(t)/g'(t)$와 $f(t)/g(t)$의 의미는
각각 순간변화율(파란색)과 평균변화율(빨간색)이다.

여기서 로피탈의 정리는 극한에 관한 것인데 $t$를 어떤 $\alpha$로 보내주는 것에 관한 것이다. 그림 1 또는 2에서 $\alpha$에 대한 극한을 취해준다는 것은 곡선상의 어디엔가 있는 $(x,y)$로 접근하겠다는 의미로 해석할 수 있다.

이 때 $t\rightarrow \alpha$로 접근할 때 시시각각 순간 변화율과 평균 변화율이 변하는 것을 확인할 수 있다.

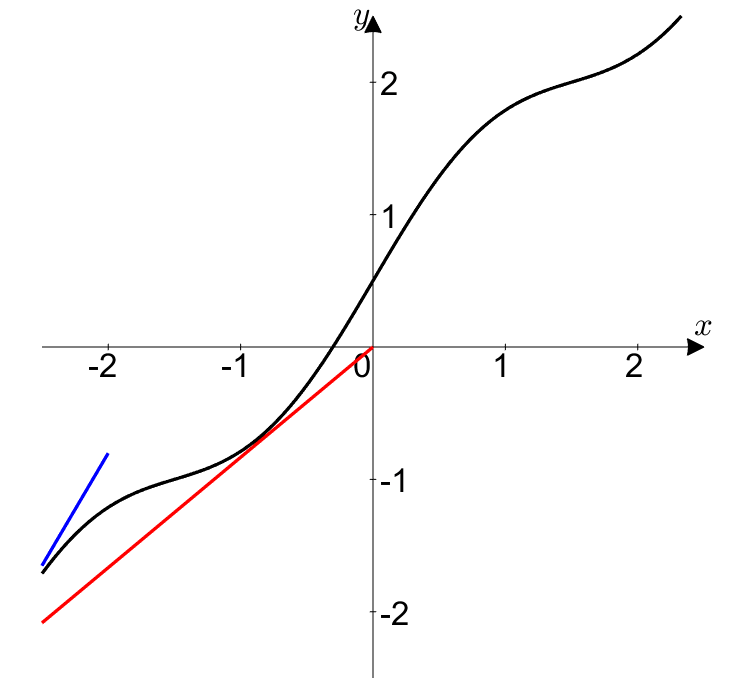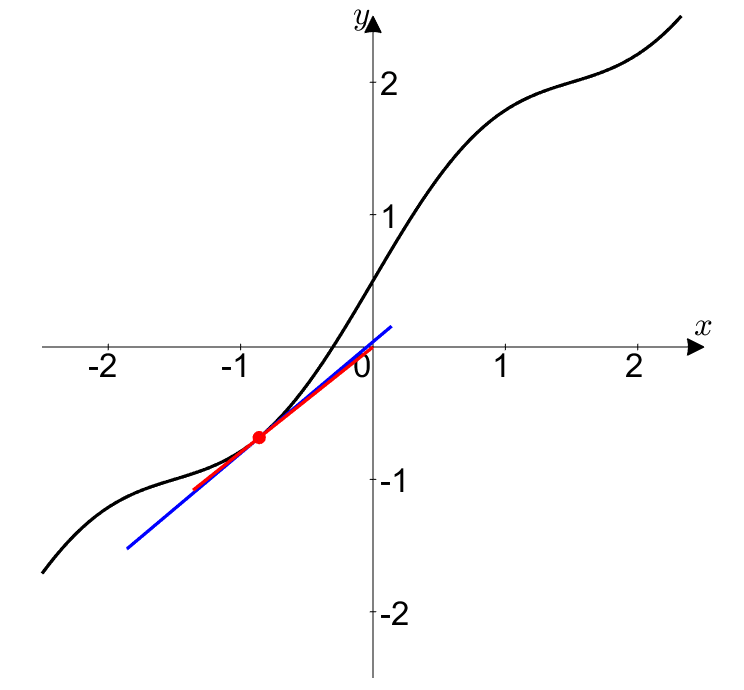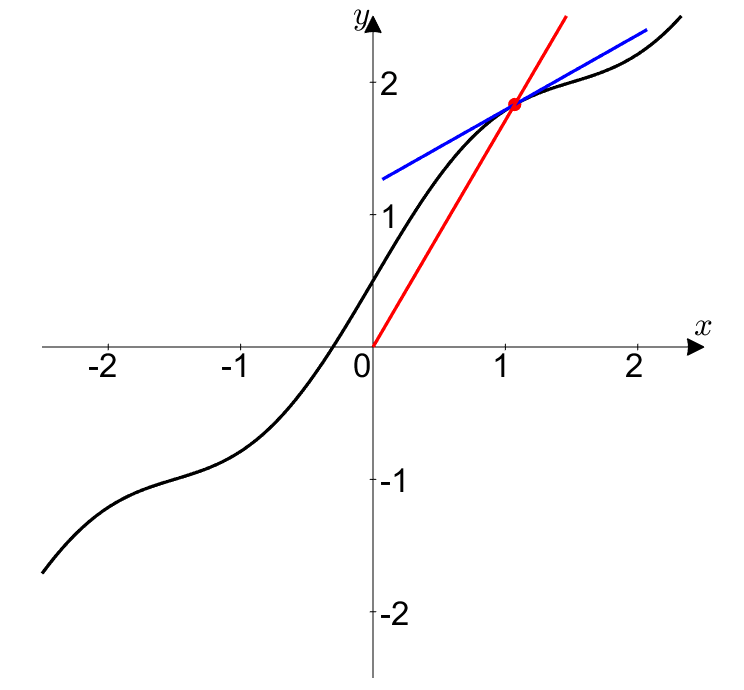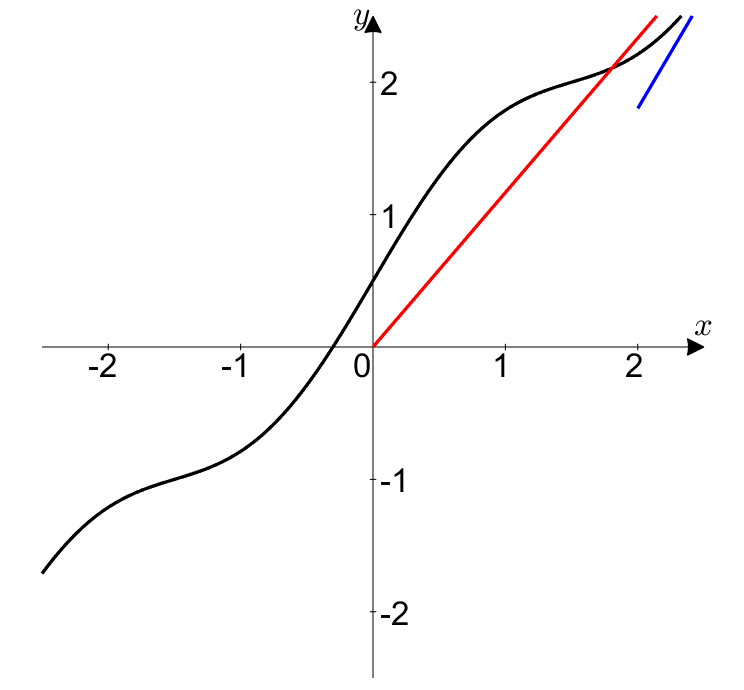
그림 3. $t\rightarrow \alpha$로 접근하겠다는 것은
빨간점을 곡선상의 어디엔가 있는 $(x,y)$로 접근시키겠다는 의미와 같으며,
시시각각 순간 변화율(파란색)과 평균 변화율(빨간색)이 변한다.

그렇다면 우리는 곡선 상의 어떤 $(x,y)$에 빨간점을 접근시켜주어야 할까?

0/0 꼴인 경우

DEFINITION 1에서 확인한 로피탈의 정리를 다시 생각해보면, 로피탈의 정리는 0/0 꼴 혹은 $\infty / \infty$ 꼴로 정해진 식에 대해서만 성립된다. 이번에는 먼저 0/0 꼴인 경우에 대해 알아보자.

0/0 꼴이 의미하는 것은 $t\rightarrow \alpha$로 향할 때 $f(t), g(t)$이 0으로 수렴한다는 것을 의미한다.

즉, 아래 그림 4와 같이 $(x,y)=(g(t), f(t))$와 같이 정의된 곡선은 $x=g(t)$의 극한 값이 0으로 향할 때 $y=f(t)$의 극한 값도 0으로 향해야 한다.

쉽게 말해, (0,0)을 통과해야 한다. (조금 더 엄밀하게는 꼭 (0,0)을 통과하지 않아도 괜찮고 극한값이 모두 0이기만 하면 된다.)

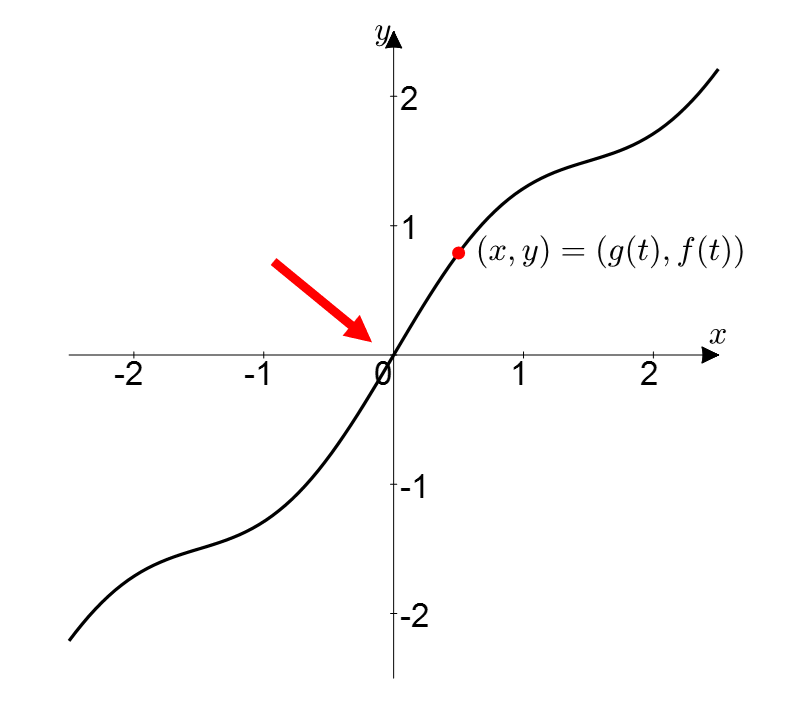
그림 4. 0/0 꼴인 경우의 로피탈 정리를 이해하기 위한 곡선의 형태

이 때, $t\rightarrow \alpha$인 경우 $f’(t)/g’(t)$의 극한값(즉, 순간 기울기)이 $L$로 수렴한다고 하자.

그러면, $f(t)/g(t)$(즉, 평균 기울기)의 값은 같아질까?

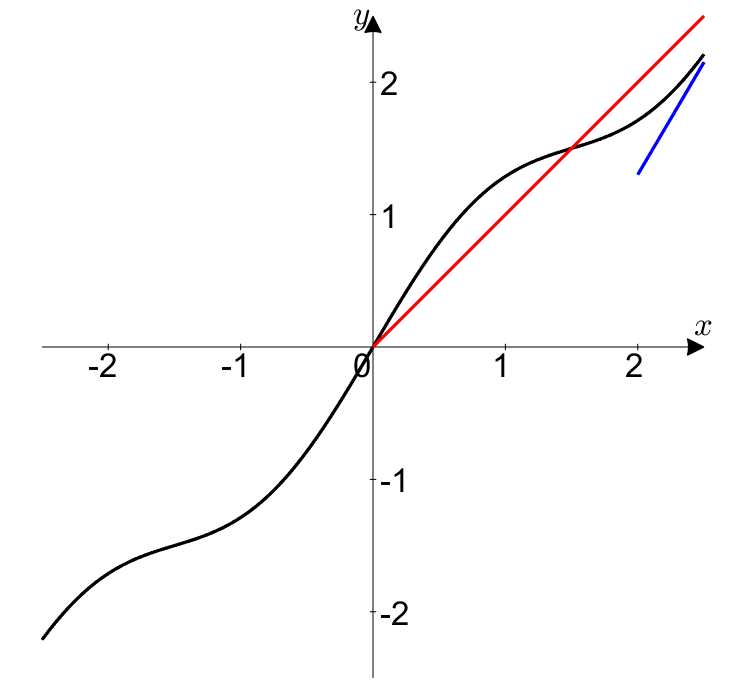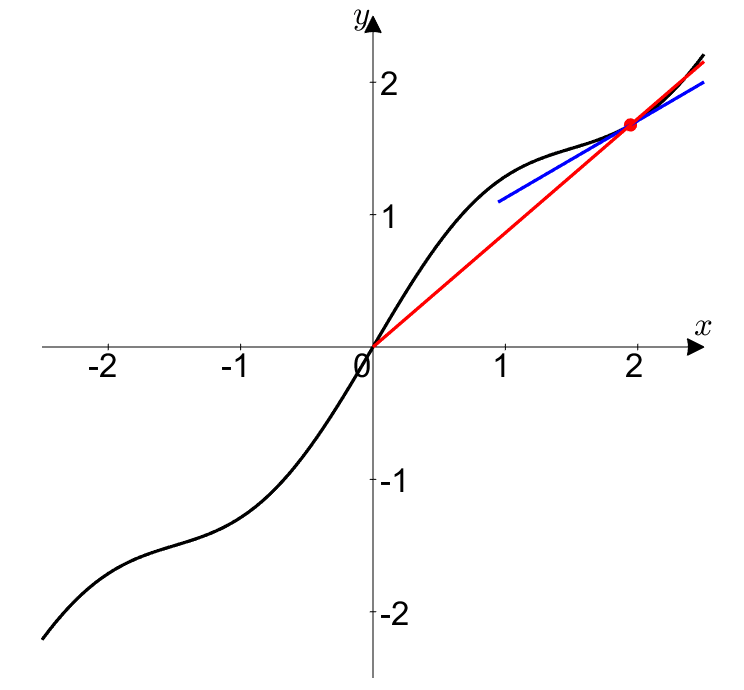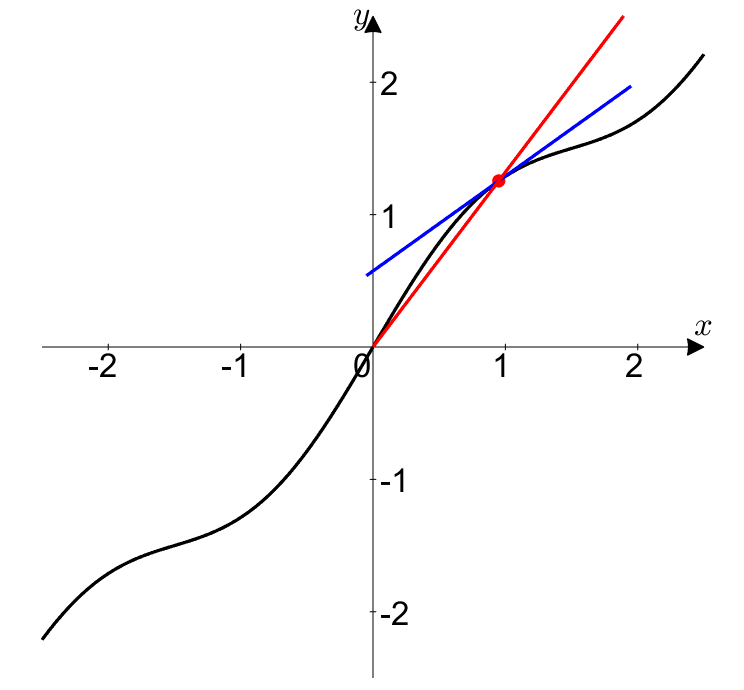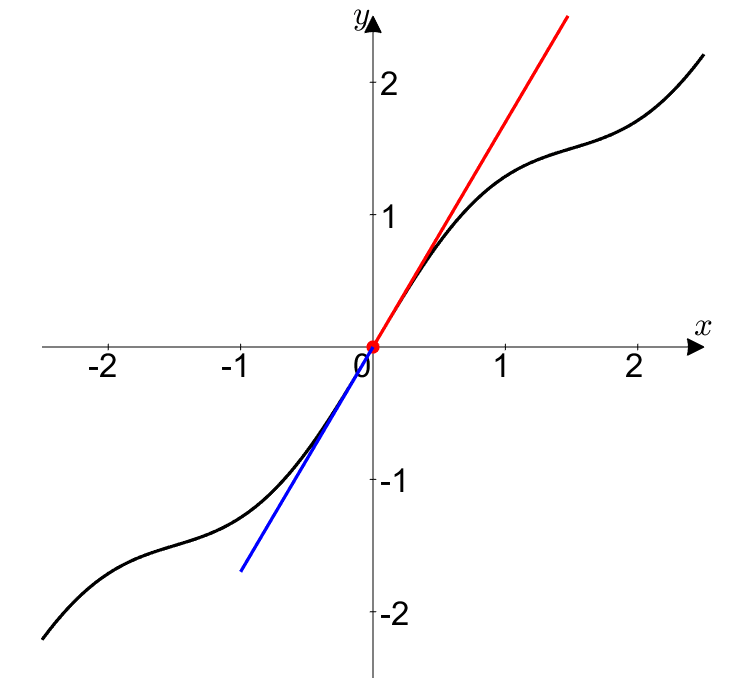
그림 5. 0/0 꼴인 경우 $f(t)$와 $g(t)$ 모두 0으로 향하는 극한을 취해주면 순간 기울기와 평균 기울기가 같아진다.

즉, $0/0$꼴에서 로피탈의 정리는 다음에 대해 말해주고 있는 것이다.

$(0,0)$에서 순간 기울기가 $L$이라면, $(x,y)$가 모두 0으로 갈 때, 평균 기울기는 $L$에 매우 가까워진다.

무한대/무한대 꼴인 경우

$\infty / \infty$ 꼴인 경우 $x = g(t)$, $y=f(t)$가 모두 무한히 커질 때 정해진 값 만큼의 기울기(여기서는 $L$)를 가지는 곡선을 상정할 수 있다면 그 기하학적 의미를 파악할 수 있다.

그림 6. $\infty / \infty$ 꼴인 경우 $f(t)$와 $g(t)$ 모두 $\infty$로 향하면서 순간기울기가 $L$로 유지되는 곡선을 만든 뒤 $t\rightarrow \infty$로 극한을 취해주면 순간 기울기와 평균 기울기가 같아진다.

즉, $\infty / \infty$꼴에서 로피탈의 정리는 다음에 대해 말해주고 있는 것이다.

$(\infty,\infty)$에서 순간 기울기가 $L$이라면, $(x,y)$가 모두 $\infty$으로 갈 때, 평균 기울기는 $L$에 매우 가까워진다.

참고 문헌

• Paths and geometry of l’Hopital’s Rule, Frank J. Swenton