회전 (curl)
위키피디아에서 Curl은 ‘3차원 벡터장을 다른 3차원 벡터장으로 대응시키는 1차 미분 연산자의 하나이다.’라고만 정의되어 있는데 이런 수학적으로는 맞을지 몰라도 처음 보는 이로 하여금 도저히 납득할 수 없도록 만드는 정의로는 curl에 대한 어떤 것도 알기 힘들다.
필자가 생각하는 Curl의 수학적 정의는 다음과 같다. 물론 엄밀한 수학적 정의는 아닐 것이다. ‘Curl은 벡터장 내에서 임의의 한 점 의 매우 작은 공간이 주변의 벡터로 인해 발생하는 회전 정도를 측정하는 연산자이다.’
또 다른 방식으로 생각해보면 ‘임의의 점 $(x,y)$에서 벡터장이 향하는 정규화 시킨 수직 방향으로의 변화량을 확인한 것’이라고도 생각할 수 있을 것 같다.
curl이 사용되는 예시 1: 강물 위의 막대기
curl의 경우는 개념이 divergence 보다 조~금 더 어렵기 때문에 정~말 쉬운 예시부터 한번 확인해보도록 하자.
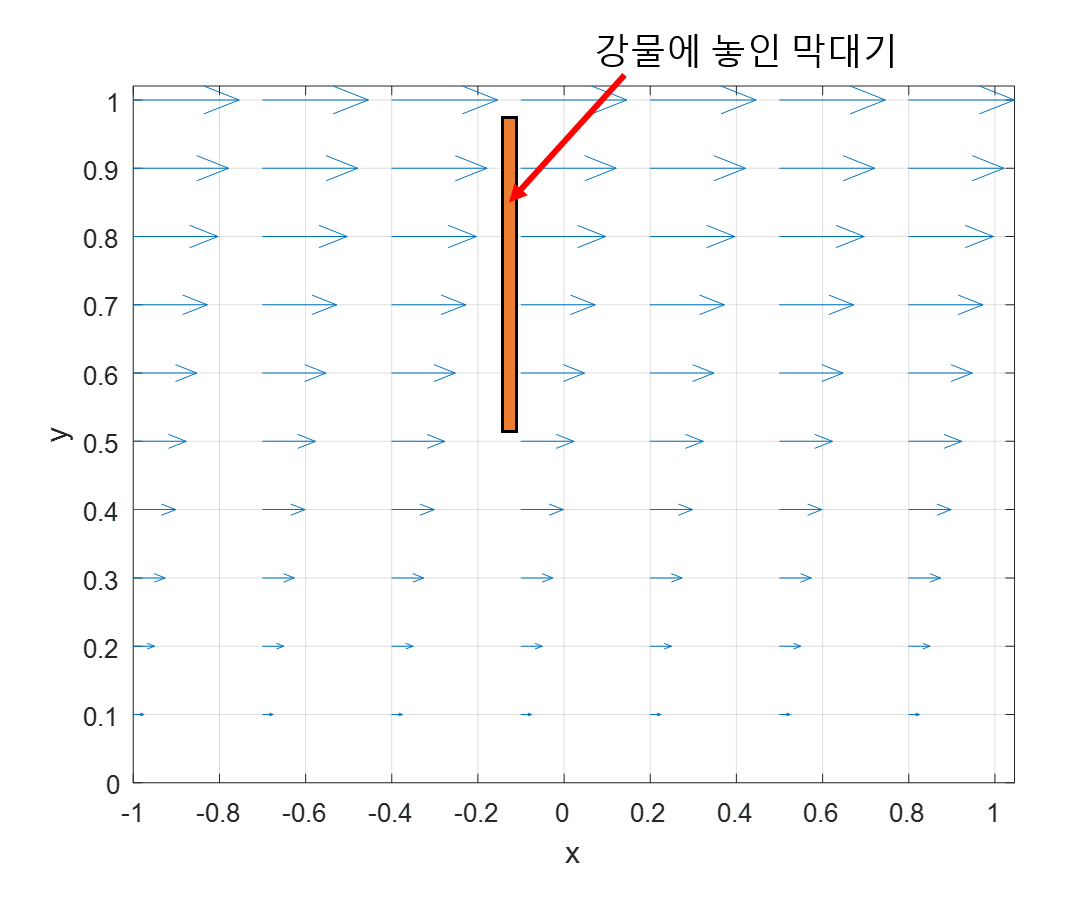
그림 1 흘러가는 강물에 막대기가 위와 같이 놓여있다고 가정하자. 각 화살표는 강물의 유속을 나타낸다.
그림 1은 흘러가는 강물에 놓인 막대기를 표시하고 있다. 즉, 그림 1에서 표시한 벡터장의 벡터 함수는
\[f(x,y) = y\hat{i}\]이다. 지금은 벡터장의 함수가 어떤지는 크게 중요하지 않으니 직관적으로 curl이 말하고자 하는 것이 무엇인지만 알아보도록 하자.
막대기의 각 부위에서 받는 유속은 서로 다르기 때문에 시계 방향으로 회전할 것이다. 그런데 만약 막대기가 그림 2 처럼 유속의 방향과 같은 방향으로 놓여있다고 하면 그 막대기는 회전할까? 그렇지 않을 것이다.
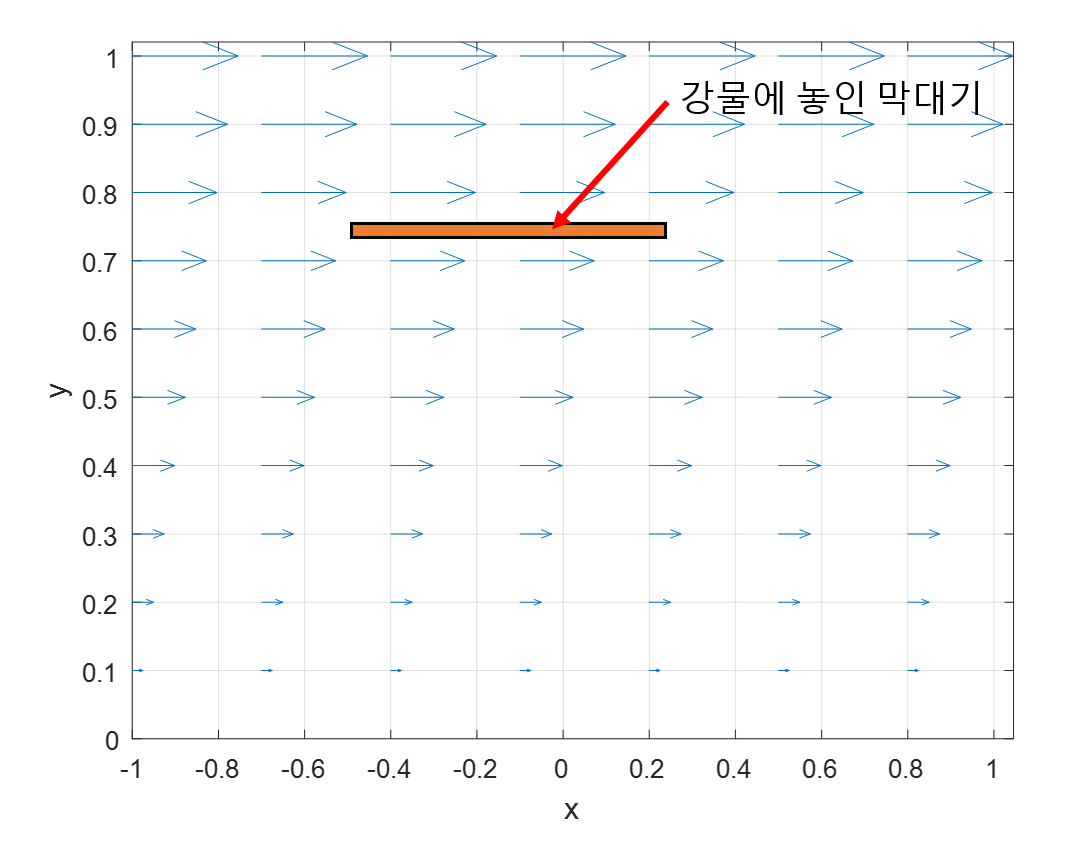
그림 2 강물의 흐름과 수평한 방향으로 놓여있는 막대기는 회전하지 않는다.
curl이 사용되는 예시 2: 강물의 와류
curl이 사용될 수 있는 예시를 하나 더 들어보자면, 강물 위의 와류를 생각해볼 수 있을 것 같다.
아래의 그림 3을 보면 (0,0)과 (4,5)에 와류가 형성되어 있는 것을 볼 수 있다.
curl에서 중요한 개념 중 하나는 회전의 방향인데, 두 개의 와류는 방향이 다르다는 것 또한 알 수 있다.
(0,0)에 형성된 와류는 시계 반대방향으로 돌고 있으며, (4,5)에 형성된 와류는 시계 방향으로 돌고 있다는 것을 알 수 있다.
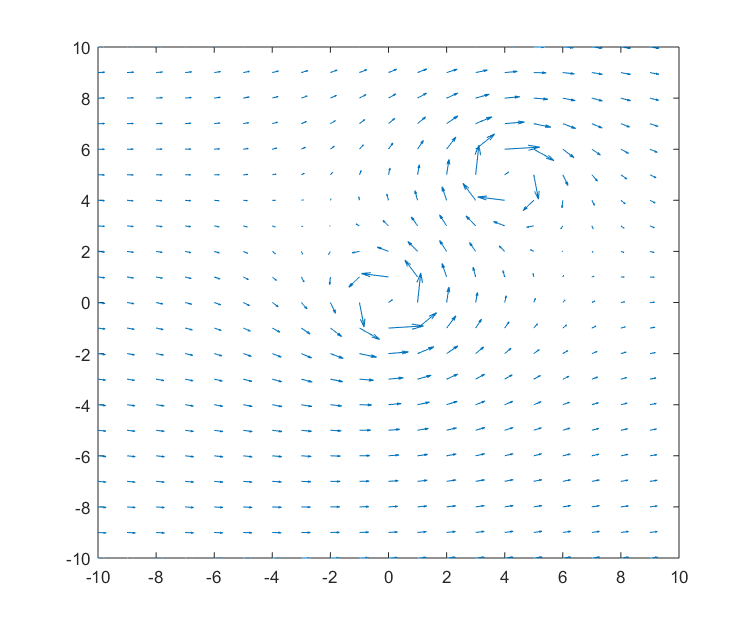
그림 3 강물의 특정 포인트에 형성된 와류
강물 위에 particle을 띄우게 되면 다음과 같은 식으로 와류가 형성된 곳에서는 particle들이 회전하는 것을 확인할 수 있다.
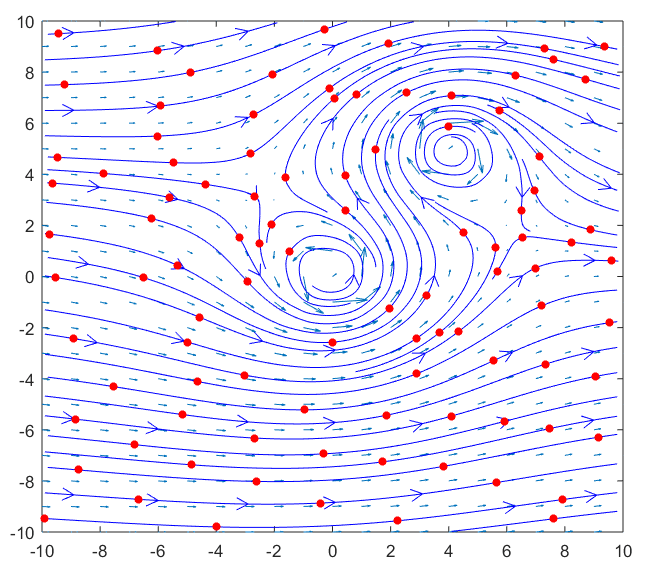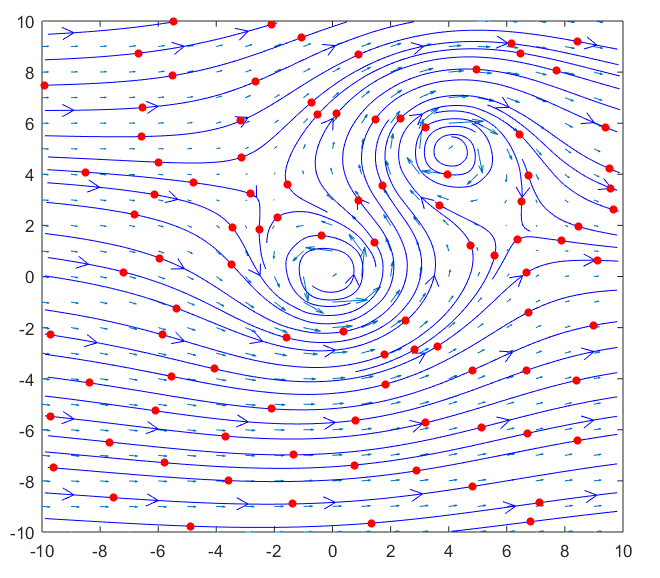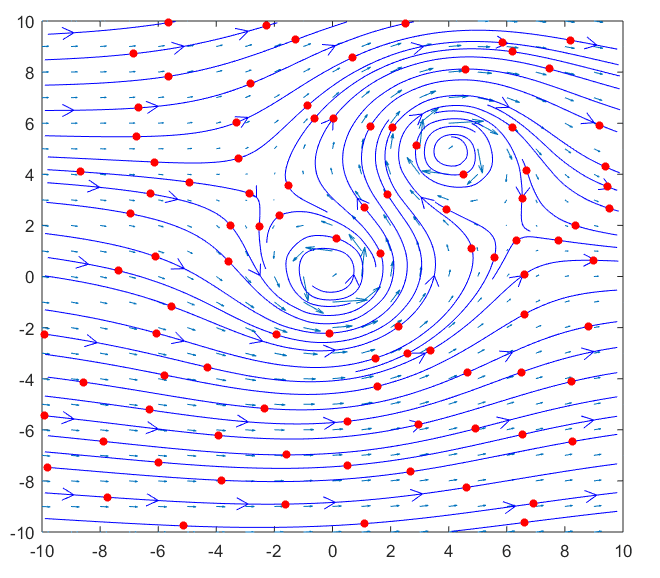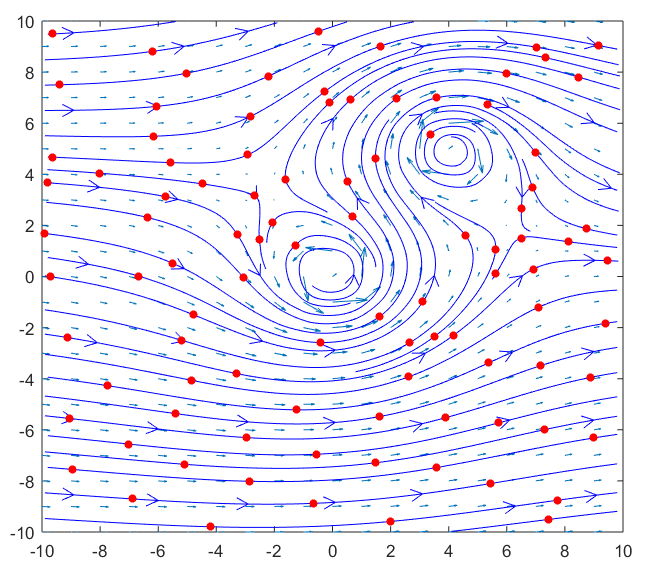
그림 4 와류가 있는 강물에서의 particle의 움직임
curl을 이용하면 그림 3, 4에서 처럼 각각의 포인트에서 회전력이 다를 때, 모든 위치에서의 회전력을 수치화 시켜줄 수 있다.
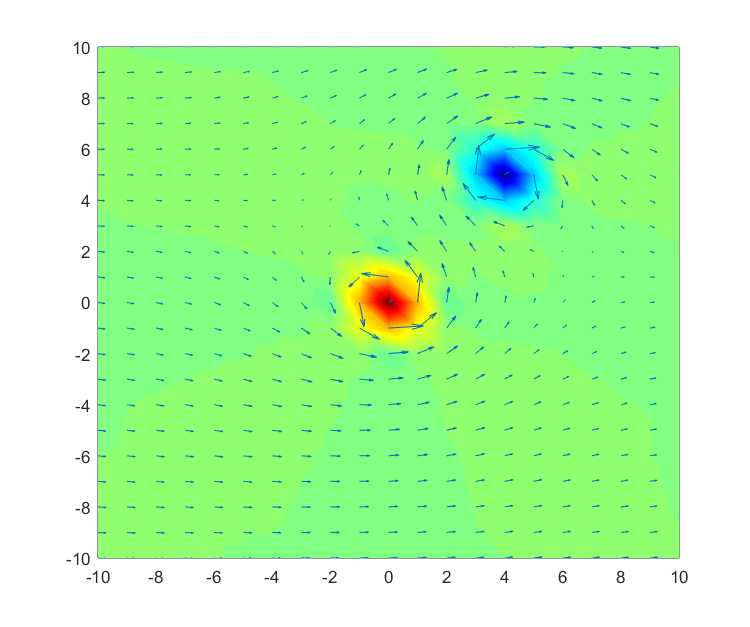
그림 5 강물의 모든 포인트의 회전력을 수치로 나타낸 것. 빨간색은 양수, 파란색은 음수이며, 초록색은 0에 가까운 회전력을 가지는 영역임.
curl은 미소 면적이 받는 회전력
divergence와 마찬가지로 curl도 매우 작은 면적이 받는 회전력을 나타내는 것이다.
macro level에서 보는 것이 아니라 micro level에서 보고자 하는 것은 macro level에서는 임의의 막대기에 들러붙는 벡터가 무한개가 존재하기 때문이다.
따라서 미소 면적이 주변의 벡터에 의해 받는 회전량이 얼마인지 알아보고자 하는 것은 divergence를 공부할 때 확인한 것과 같은 맥락이라고 할 수 있다. 이제 미소 면적이 받는 curl을 수학적으로 생각해보도록 하자.
Curl의 공식 유도
아래와 같이 미소 면적을 생각해보자. 미소 면적의 중심 좌표는 $(x,y)$이고 너비는 $2\Delta x$, 높이는 $2\Delta y$이다. 이 때 그림 3에서와 같이 각 변의 중점을 ①, ②, ③, ④와 같이 명명하도록 하자.
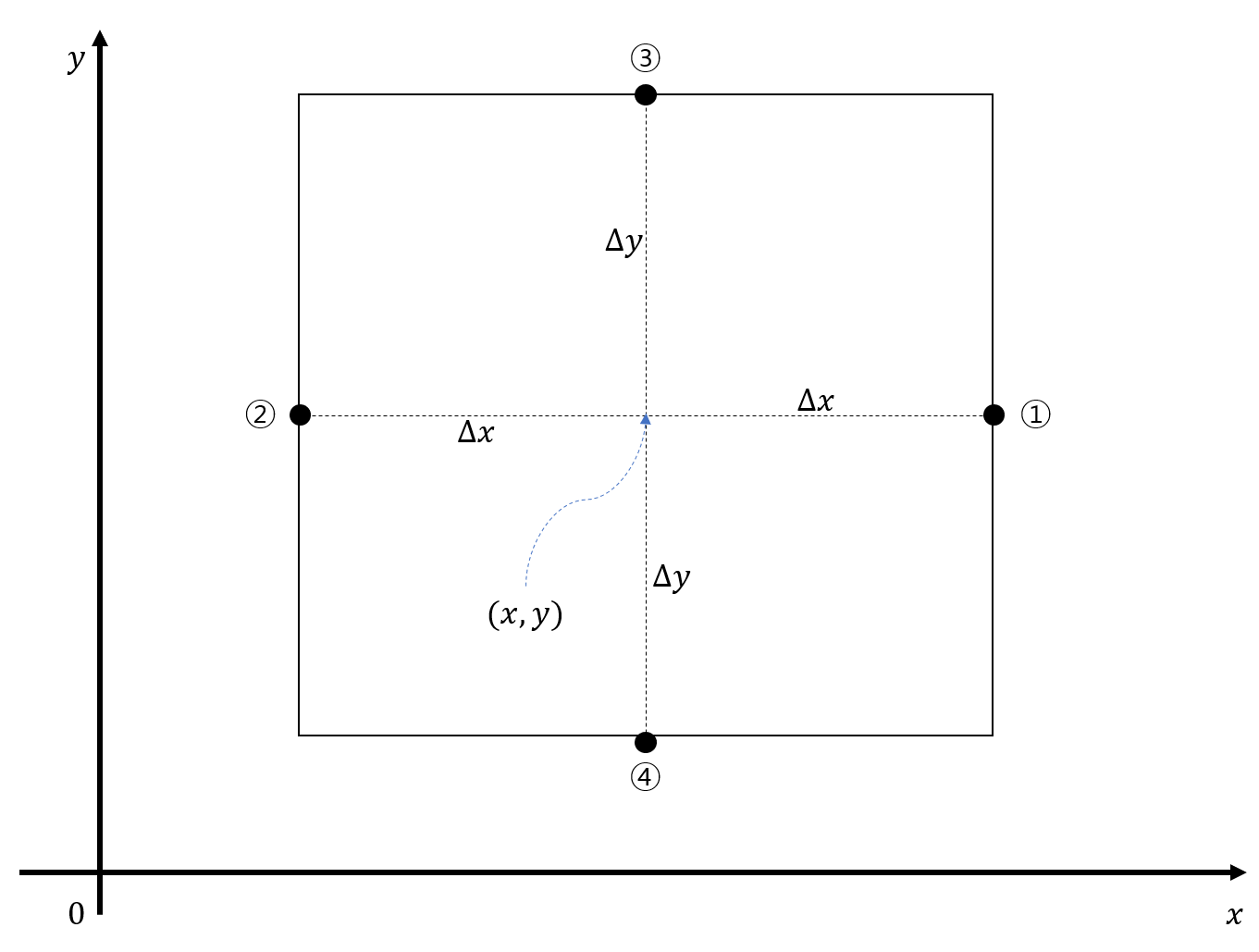
그림 6 xy 평면 상의 미소 면적
이제 우리는 이 미소 면적이 받는 회전량을 구하려고 한다. 수학에서는 반시계방향이 정 방향 회전인데, 반 시계 방향 회전이 되는 것을 생각하려면 두 가지 경우를 모두 생각해야 한다.
그것은 ①-② 막대기가 받는 힘에 의해 생기는 회전과 ③-④ 막대기가 받는 힘에 의해 생기는 회전이다.
이 때 ①-② 막대기가 회전할 때는 $2\Delta y$만큼의 폭은 없다고 생각하게 될 것이고,
③-④ 막대기가 회전할 때는 $2\Delta x$만큼의 폭은 없다고 생각하여서 두 번의 회전에 의해 구한 회전량을 superposition할 것이다.
회전은 방향을 고려해줘야 하기 때문에 벡터로 표현되고, 벡터는 중첩의 원리를 적용할 수 있기 때문이다.
따라서 증명은 두 단계로 나뉜다. 이후부터는 $xy$ 평면상에 $f(x,y)=P(x,y)\hat{i}+Q(x,y)\hat{j}$라는 벡터장이 형성되어 있다고 생각하도록 한다.
또, 미소 면적의 회전 방향은 시계 반대방향이라고 가정하자.
I) ①-② 막대기가 회전하는 양
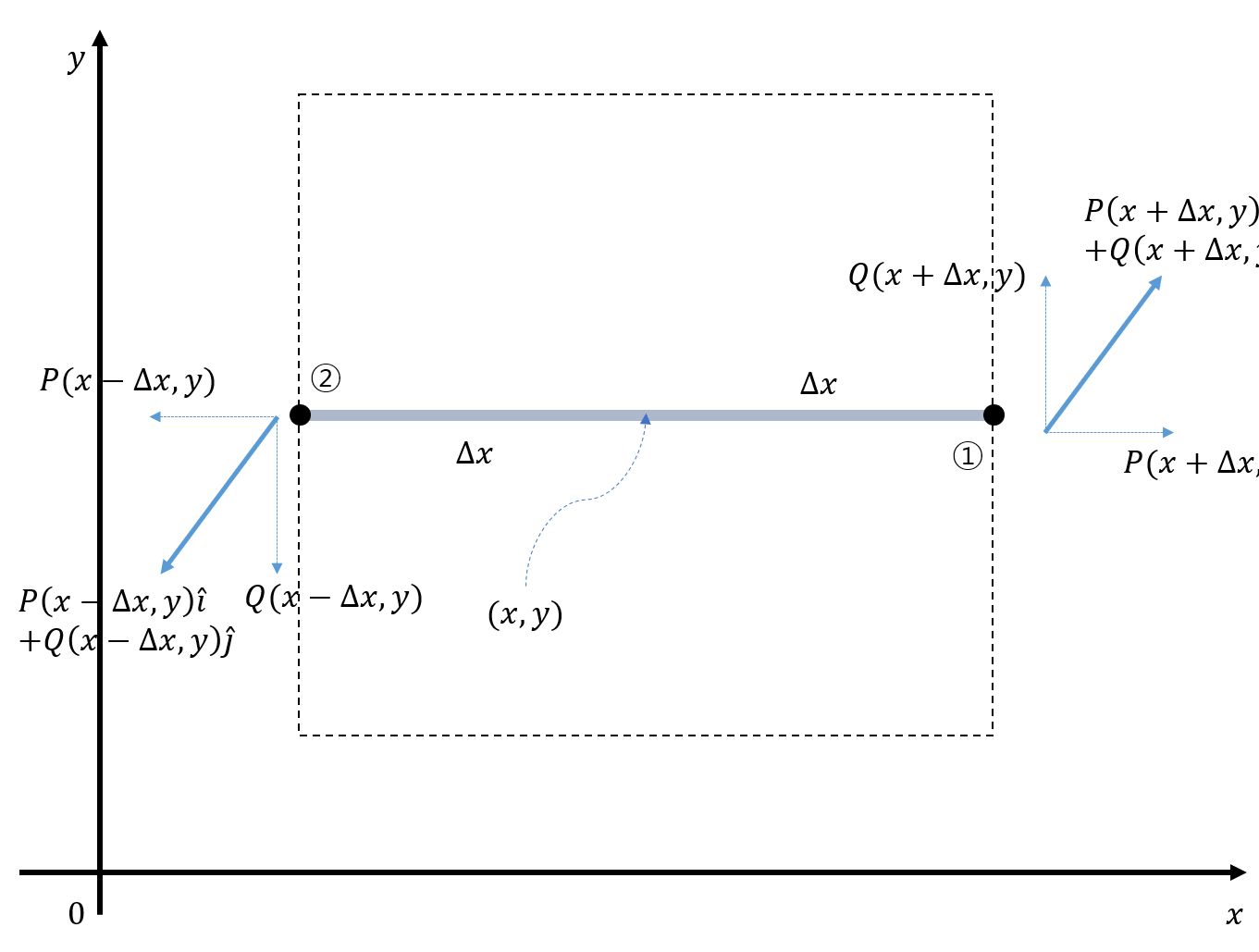
그림 7 ①-② 막대기가 회전할 때 점 ①과 점 ②에 적용되는 벡터를 표시한 그림
벡터장 $f(x,y)$가 힘을 나타낸다고 하자.
①-② 막대기가 회전할 때 받는 회전력만 고려하려면 그림 7에서 확인할 수 있듯이
점 ①과 점 ②가 받는 방향의 net force를 고려해주면 된다. 따라서 ①-② 막대기가 회전하기 위해 받는 net force는
\[Q(x+\Delta x, y) - Q(x-\Delta x, y)\]이다.
그렇다면 단위 길이만큼 받는 회전력은 ①-② 막대기의 길이는 $2\Delta x$이므로
\[\frac{Q(x+\Delta x, y) - Q(x-\Delta x, y)}{2\Delta x}\]가 될 것이다.
가정에서 이 면적은 실제로는 미소 면적을 뜻하기 때문에 $\Delta x$를 매우 작게 만들어주어야 한다.
따라서 미소 길이의 ①-② 막대기가 받는 단위 길이만큼의 회전력은
\[\lim_{\Delta x \rightarrow 0}\frac{Q(x+\Delta x, y) - Q(x-\Delta x, y)}{2\Delta x} = \frac{\partial Q}{\partial x}\]이다. 이 때 회전하는 방향은 시계 반대 방향이라고 가정했고 그 때는 회전의 축은 $\hat{k}$방향이다. 따라서 ①-② 막대기의 회전을 표현하는 벡터는
\[\frac{\partial Q}{\partial x}\hat{k}\]이다.
II) ③-④ 막대기가 회전하는 양
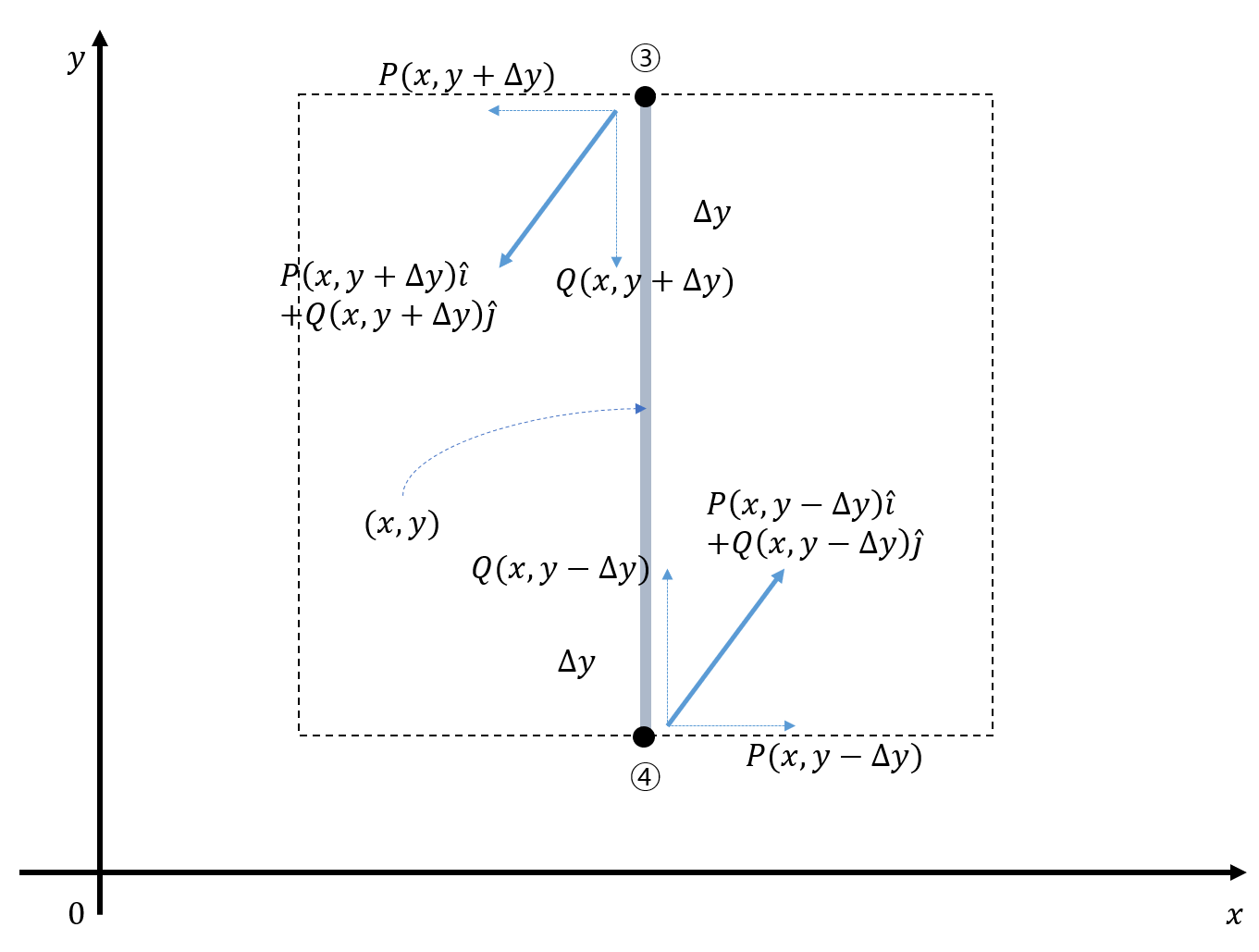
그림 8 ③-④ 막대기가 회전할 때 점 ③과 점 ④에 적용되는 벡터를 표시한 그림
벡터장 $f(x,y)$ 가 힘을 나타낸다고 하면, ③-④ 막대기가 회전할 때 받는 회전력만 고려하려면
그림 8에서 확인할 수 있듯이 점 ③과 점 ④가 받는 방향의 net force를 고려해주면 된다.
또, 막대기는 반시계 방향으로 회전하고 있다고 가정했기 때문에 그것을 고려한다면 ③-④ 막대기가 회전하기 위해 받는 net force는
\[P(x, y-\Delta y) - P(x, y+\Delta y)\]이다.
그렇다면 단위 길이만큼 받는 회전력은 ③-④ 막대기의 길이는 $2\Delta y$이므로
\[\frac{P(x, y-\Delta y) - P(x, y+\Delta y)}{2\Delta y}\]가 될 것이다.
가정에서 이 길이는 실제로는 미소 길이를 뜻하기 때문에 $\Delta y$를 매우 작게 만들어주어야 한다.
따라서 미소 길이의 ③-④ 막대기가 받는 단위 길이만큼의 회전력은
\[\lim_{\Delta y \rightarrow 0}\frac{P(x, y-\Delta y) - P(x, y+\Delta y)}{2\Delta y} = -\frac{\partial P}{\partial y}\]이다. 이 때 회전하는 방향은 시계 반대 방향이라고 가정했고 그 때는 회전의 축은 $\hat{k}$방향이다.
따라서 ③-④ 막대기의 회전을 표현하는 벡터는
\[-\frac{\partial P}{\partial y}\hat{k}\]이다.
그러므로 I) 과 II)로부터 ①,②,③,④ 포인트에 작용하는 벡터에 의해 이 미소 면적이 받는 회전 벡터의 총 합은
\[\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\hat{k}\]이다.
만약 3차원 공간에서 미소 체적의 curl을 구하려고 하면 yz 평면, zx 평면에서 마찬가지의 방법으로 구할 수 있으며 벡터장 $f(x,y,z)$가 $f(x,y,z)=P(x,y,z)\hat{i}+Q(x,y,z)\hat{j}+R(x,y,z)\hat{k}$라고 하면 그 값은
\[curl(f) = \left(\frac{\partial}{\partial y}R - \frac{\partial}{\partial z}Q \right)\hat{i} -\left(\frac{\partial}{\partial x}R - \frac{\partial}{\partial z}P \right)\hat{j} +\left(\frac{\partial}{\partial x}Q - \frac{\partial}{\partial y}P \right)\hat{k}\]이다.
이것은 다음과 같이 3차원 벡터의 determinant로도 표현할 수 있다.
\[curl(f) = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \\ \end{vmatrix}\]과 같다. 이렇게 표기하게 되면 이것은 del 연산자를 이용해 이렇게 표시할 수도 있다.
\[curl(f) = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ P & Q & R \\ \end{vmatrix} = \nabla \times f\]이렇게 놓고 생각해보면 $\nabla \times f$의 의미는 임의의 점 $(x,y)$에서 벡터장이 향하는 정규화 시킨 수직 방향으로의 변화량이라고 설명하는 것을 이해할 수 있을 것이다.
※ MATLAB 코드는 공돌이의 수학정리노트 Github Repo에서 받으실 수 있습니다.
$\Rightarrow$ 공돌이의 수학정리노트 Github Repo