※ 본 포스팅의 내용은 수학적인 엄밀성 보다는 그린 함수의 개념에 더 쉽게 다가가기 위해 작성한 것입니다. 혹시나 수학적으로 치명적인 오류가 있다면 꼭 조언 부탁드립니다.

Prerequisites

그린 함수를 이용한 미분방정식의 해법을 이해하기 위해서는 다음의 내용에 대해 이해하고 오시는 것이 좋습니다.

• 행렬 곱에 대한 또 다른 시각
• 행벡터의 의미와 벡터의 내적
• 선형 연산자와 함수 공간

선형 연산자의 역행렬을 생각할 수 있을까?

선형 연산자와 함수 공간 편에서는 함수를 벡터로 취급할 수 있음을 알아보았고 미분 연산자의 관점에서 미분 방정식을 해석했다. 또, 선형 연산자란 선형대수학에서 공부한 행렬의 개념을 확장시킨 것으로, 함수를 입력 받으면 또 다른 함수를 출력해주는 것이라고 배웠다.

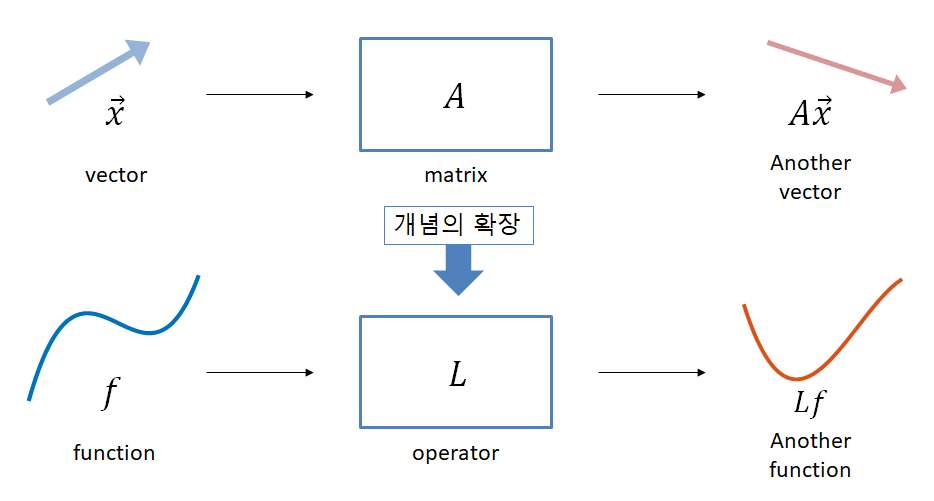
그림 1. 연산자(operator)란 함수를 입력으로 받고 또 다른 함수를 출력해주는 함수이다. 이 개념은 선형대수학의 행렬을 확장시킨 개념이라고 볼 수 있다.

이번에는 그러면 역행렬에 대해 생각해보자.

역행렬은 아래와 같이 정의되는 행렬이다. 임의의 정사각 행렬(square matrix) $A$와 벡터 $x$, $b$에 대해 다음이 성립한다고 하자.

\[Ax=b\]

만약 $A$라는 행렬이 역행렬을 가진다고 하면 역행렬 $B$는 다음과 같은 성질을 만족하는 행렬이다.

\[AB=I\]

여기서 $I$는 단위 행렬이다.

우리는 보통 역행렬을 $A^{-1}$라고들 많이 쓰지만 여기선 역행렬 또한 일종의 행렬임을 강조하고자 썼다.

연산자 이론을 처음 배울 때 강조했던 것 처럼 어떤 개념을 다른 필드로 확장시키기 위해선 의심해보고 또 의심해봐야 한다. 그리고 확장 시키고자 하는 개념의 본래적 의미가 무엇이었는지 수차례 고민해보아야 한다.

우리는 행렬곱과 역행렬의 의미를 다시 한번 생각해보자.

행렬곱과 역행렬의 의미

우리는 행렬 곱에 대해 다시 한번 생각해보자.

$AB=I$라는 식을 보면 다음과 같은 일들이 일어나는 것임을 알 수 있다.

• $A$라는 연산자가 $B$의 첫번째 열에 적용되면 첫 번째 단위 기저벡터가 출력된다.
• $A$라는 연산자가 $B$의 두번째 열에 적용되면 두 번째 단위 기저벡터가 출력된다.

\[\vdots\notag\]

• $A$라는 연산자가 $B$의 마지막 열에 적용되면 마지막 단위 기저벡터가 출력된다.

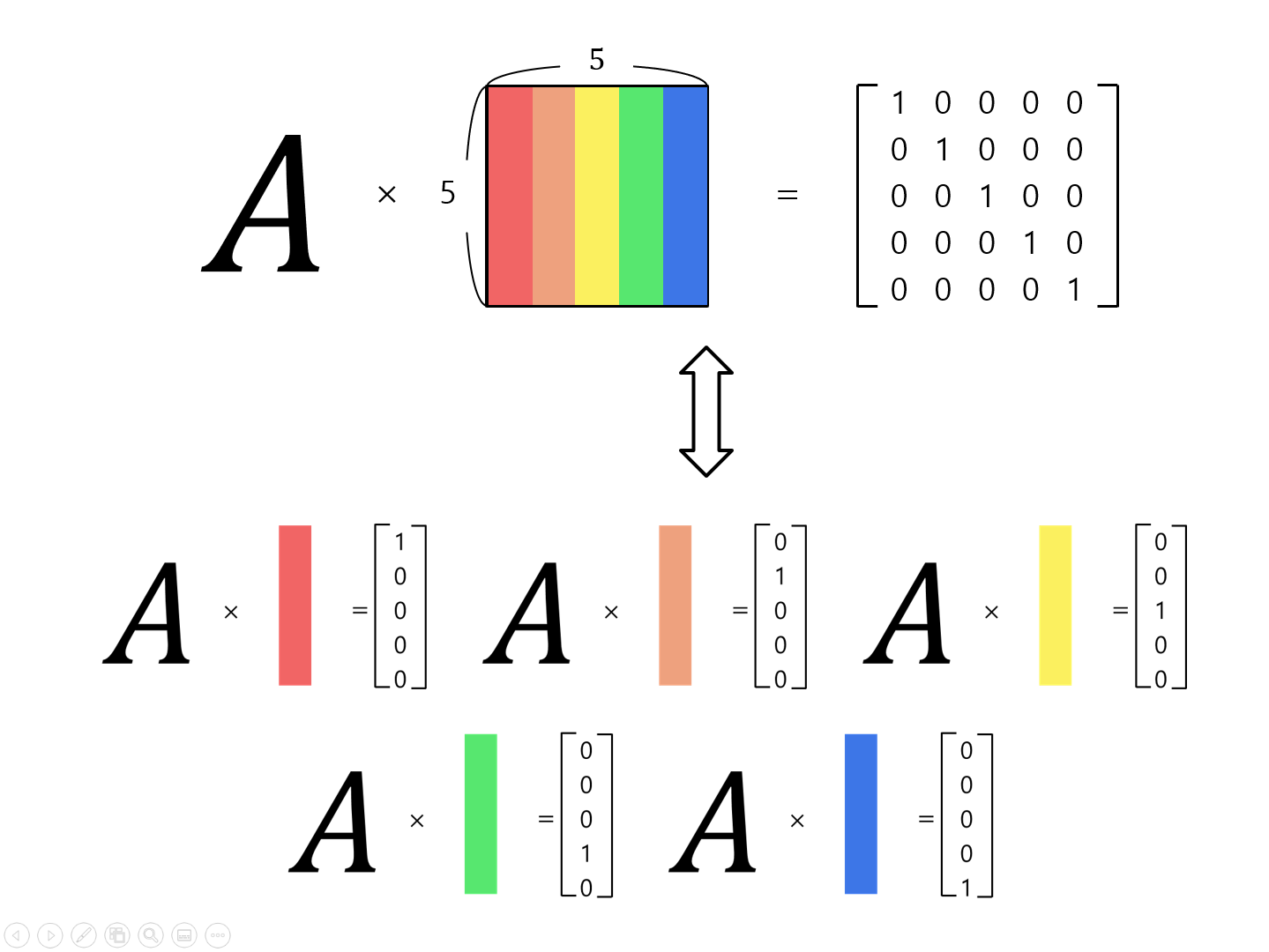
그림 2. 행렬 곱셈 연산이 수행되는 두 행렬에 대해 두 번째 행렬이 앞선 행렬의 역행렬이 되려면 앞에 곱해지는 행렬이 뒤에 곱해지는 행렬의 각각의 열에 작용해 각 순번에 해당하는 단위 기저벡터를 출력해야 한다.

선형 연산자와 함수 공간 편에서는 함수를 벡터로 취급할 수 있음을 설명하였다.

그러니까, 만약 $AB=I$라는 $B$ 행렬이 존재할 수 있다면 $B$ 행렬은 열벡터를 쌓아 만든 개념으로 볼 수 있는 것이므로 함수해석학에서 행렬 $B$에 대응하는 개념은 함수를 연속적으로 쌓아 만든 것으로 볼 수 있다.

다시 말해 원래의 독립변수가 아닌 또 다른 독립변수에 대응되는 함수들을 쭉 나열해둔 것이어야 한다.

$L$은 선형연산자, $u(x)$와 $f(x)$는 $x\in[a,b]$에서 정의된 함수라고 생각해보자. 이 때, 다음이 성립한다고 하자.

\[Lu=f\]

그리고 우리가 생각해낼 ‘함수의 나열’을 다음과 같은 기호로 써보자.

\[G(x,y)\]

이런 기호로 새로운 함수 뭉치들을 써낸 것은 $y$ 역시 $y\in[a,b]$의 정의역에서 정의되는 새로운 독립변수로 쓴 것이고, 새로운 $y$축을 따라 $G(x;y)$를 쌓아줄 것이기 때문이다.

그러면 우리는 $L$이라는 연산자가 $y$를 따라가면서 적용될 때 다음과 같은 일이 일어나야 역행렬이 해주는 일과 유사한 일을 적용시킨다는 것을 알 수 있다.

• $L$이라는 연산자가 $G(x, y)$의 $y$의 첫 번째 값($a$)에 대응되는 함수에 적용되면 첫 번째 단위 기저벡터에 대응되는 함수가 출력된다.
• $L$이라는 연산자가 $G(x, y)$의 $y$의 두 번째 값($a$의 바로 옆 값)에 대응되는 함수에 적용되면 두 번째 단위 기저벡터에 대응되는 함수가 출력된다.

\[\vdots\notag\]

• $L$이라는 연산자가 $G(x, y)$의 $y$의 마지막 값($b$)에 대응되는 함수에 적용되면 마지막 단위 기저벡터에 대응되는 함수가 출력된다.

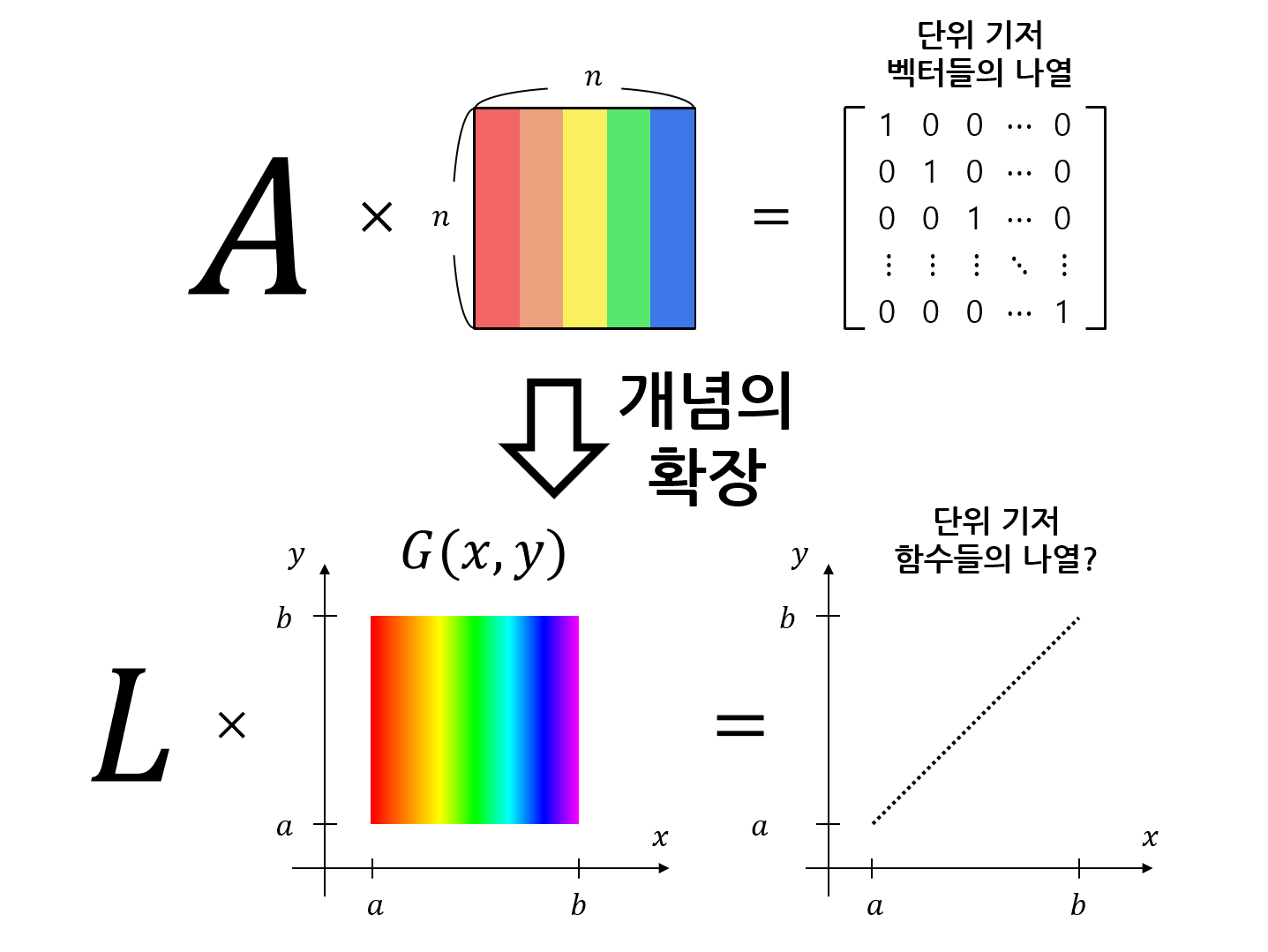
그림 3. 어떤 선형 연산자 $L$에 대해 역행렬에 대응되는 함수 $G(x,y)$를 얻으려면 연산자가 각 순번 $y$에 대응하는 함수 $G(x, y)$에 적용되었을 때 단위 기저벡터에 대응하는 함수를 출력해줄 수 있어야 한다.

그렇다면 우리는 단위 기저 벡터에 대응되는 함수의 개념을 생각해보아야 한다. 이 개념은 디랙 델타 함수라는 개념에서부터 찾을 수 있다.

단위 기저 함수?

디랙 델타 함수의 motivation

우리는 단위 기저 벡터에 대해 생각해보기 위해 먼저 단위 기저 벡터라는 것이 어떤 것이었는지 알아보고 이 개념을 함수 공간에 확장시켜보도록 하자.

가장 간단한 단위 기저 벡터는 보통 표준 기저(standard basis)라고 부르는 것들이다. 2차원 벡터 공간에서는 $\hat{i}$, $\hat{j}$라고 단위 기저 벡터를 부르며 각각은

\[\hat{i}=\begin{bmatrix}1\\0\end{bmatrix}\] \[\hat{j}=\begin{bmatrix}0\\1\end{bmatrix}\]

이다.

여기서 기저 벡터의 기능은 무엇이라고 할 수 있을까? 그것은 임의의 벡터를 기저벡터의 선형결합으로 표현하는데 있다.

가령, 임의의 벡터

\[\begin{bmatrix}a\\b\end{bmatrix}\]

는 다음과 같이 위의 두 기저벡터 $\hat{i}$와 $\hat{j}$의 선형결합으로 표현할 수 있다.

\[\begin{bmatrix}a\\b\end{bmatrix} = a\begin{bmatrix}1 \\ 0 \end{bmatrix}+b\begin{bmatrix}0 \\ 1 \end{bmatrix}=a\hat{i}+b\hat{j}\]

그러다보니 다음과 같이 임의의 벡터를 기저 벡터와 내적해주면 기저벡터가 가지고 있는 성분량이 나오게 되는 것이다.

가령, 임의의 벡터 $[a,b]^T$에 대해 $\hat{i}$ 기저벡터와의 내적은 $a$라는 값을 뽑아준다.

\[\text{dot}(\begin{bmatrix}a\\b \end{bmatrix}, \begin{bmatrix}1\\0 \end{bmatrix})=a\]

그리고 벡터는 숫자들의 나열이라고도 볼 수 있다. 그래서 더 많은 숫자를 나열해볼 수도 있다.

가령, $[2, 3, 5, 1, 4]^T$라는 5차원 벡터에 대해 기저벡터 $[1, 0, 0, 0, 0]^T$과 내적해줌으로써 이 기저벡터가 $[2, 3, 5, 1, 4]^T$라는 벡터를 표현할 때 담당하는 성분량을 알 수 있게 되는 것이다.

\[\text{dot}\left(\begin{bmatrix}2\\3\\5\\1\\4\end{bmatrix}, \begin{bmatrix}1\\0\\0\\0\\0\end{bmatrix}\right) = 2\]

마찬가지 방식으로 우리도 함수의 특정 위치의 값을 뽑아오기 위해서는 내적을 해주기 위한 기저 벡터와 유사한 함수를 생각해야 한다.

함수의 내적은 구간이 적절하게 $[a,b]$와 같이 정해졌을 때 아래와 같이 정의되었다.

$x\in[a,b]$에서 정의된 함수 $f$, $g$에 대해

\[\langle f, g\rangle = \int_{a}^{b}\overline{f(x)}g(x)dx\]

여기서 $\overline{f(x)}$는 $f(x)$의 complex conjugate 이다.

만약 $f(x)=\overline{f(x)}$라면 다음과 같이도 써줄 수 있다.

\[\langle f, g\rangle = \int_{a}^{b}f(x)g(x)dx\]

즉, 함수의 내적은 적분으로 정의되므로 적분을 이용해 함수값을 뽑아내주기 위해 아래와 같은 함수를 생각해보자.

\[r(x) = \begin{cases}1/(2\epsilon),\quad -\epsilon<x<\epsilon \\ 0,\quad\quad \quad\quad \text{elsewhere}\end{cases}\]

여기서 $\epsilon$은 아주 작은 크기의 실수(real number)이다.

이 함수는 $r(x)=\overline{r(x)}$이므로 아래와 같은 적분으로 함수의 내적을 이용할 수 있을 것이다.

\[\langle r(x), f(x) \rangle =\int_{a}^{b}r(x)f(x)dx\]

이 함수는 모든 정의역 구간에서 적분했을 때 넓이는 1이므로 값을 얻고자 하는 함수 $f(x)$와 적분하면 $f(0)$ 근처의 값을 얻어올 수 있게 된다.

다시 말해 다음과 같은 내적을 생각할 수 있다는 의미이다. 만약 $x\in[a,b]$에 대해 $a\lt 0\lt b$ 인 경우를 상정한다면

\[\langle r(x), f(x)\rangle=\int_{a}^{b}r(x)f(x)dx\approx f(0)\]

이라는 것이다.

디랙 델타 함수의 출현

그런데, 문제는 $r(x)$는 적절한 너비 $2\epsilon$ 만큼에 대해 정의되어 있으므로 $f(x)$와 $r(x)$의 적분으로는 실제 $f(0)$ 값을 얻기 어려울 것이다. 따라서 우리는 $\epsilon$을 매우 작게 만들면 더 정확히 $f(x)$의 값을 위 식과 같은 내적을 통해서 얻을 수 있다는 것을 예상할 수 있다. 우리는 $\epsilon$을 작게 만들어줄 때 다음과 같은 일이 일어날 것임을 알 수 있다.

그림 4. $\epsilon$이 작아지면서 바뀌어가는 $r(x)$의 형태

따라서, 우리는 $\epsilon$이 작아질 수록 $r(x)$가 아래의 $\delta(x)$와 같은 모습을 띄게 된다는 것을 알 수 있다.

\[\delta(x)=\begin{cases}\infty,\quad x=0 \\ 0,\ \ \quad x\neq 0\end{cases}\] \[\int_{-\infty}^{\infty}\delta(x)dx = 1\]

즉, 우리는 $\epsilon$을 매우 작게 만들어줌으로써 다음과 같은 관계를 얻어낼 수 있게 된다.

\[\int_{a}^{b}\delta(x)f(x)=f(0)\]

그림 5. 디랙 델타함수와의 내적을 통해 함수의 특정 값을 얻어낼 수 있다.

또, 만약 $x=0$ 외의 다른 위치 $x_0$에서의 함수값을 얻고 싶다면 $r(x)$를 평행이동 시켜 $r(x-x_0)$과 적분해주면 될 것이다.

$x_0$가 구간 $[a, b]$ 사이에 위치한다고 가정했을 때,

\[f(x_0) \approx \int_{a}^{b}r(x-x_0)f(x)dx\]

와 같다.

여기서도 $\epsilon$을 매우 작게 만들어주면,

\[f(x_0)=\int_{a}^{b}\delta(x-x_0)f(x)dx\]

와 같이 $f(x)$의 $x_0$라는 입력에 해당하는 원소의 값을 얻어낼 수 있게 되는 것이다.

그림 6. $x=0$이 아닌 임의의 위치의 함수값을 얻고 싶다면 디랙 델타 함수를 옮겨 계산하면 된다.

결국 디랙 델타 함수는 단위 기저벡터에 대응하는 함수라고 볼 수 있다 ¹.

미분 연산자의 inverse = 그린 함수

그린 함수의 정의

앞서 고민하던 기저벡터의 개념을 디랙 델타함수를 통해 확장시킬 수 있다는 것을 알았으니 이제는 역행렬에 대응되는 함수 $G(x,y)$를 제대로 정의할 수 있게 되었다. 이 역행렬에 해당되는 $G(x,y)$는 그린 함수(Green function)라는 이름이 붙어있는데 조금 자세하게 보면 그린 함수의 정의는 다음과 같다.

구간 $x\in[a,b]$ 및 적절한 경계 조건에서 정의된 선형연산자 $L$과 함수 $u, f$에 대해서 다음이 성립한다고 하자.

\[Lu=f\]

여기서 경계조건은 다음과 같은 것일 수 있다².

\[u(a)=0, u(b)=0\]

이 때 그린 함수 $G(x, y)$는 다음과 같은 조건을 만족하는 함수이다.

\[LG= \delta(x-y)\]

여기서 $\delta(x)$는 디랙 델타 함수이다. 또, $y$ 역시 $y\in[a,b]$와 같이 정의된 변수이다.

이렇게 보면 위 식이 바로

\[AB=I\]

와 같은 꼴임을 생각할 수 있다.

즉, 대략적인 표기로

\[G(x,y) \approx L^{-1}\]

이다.

$G(x,y)$가 $L$의 inverse가 될 수 있는지 다시 한번 확인해보기 위해 위 식에서 양변에 $f(y)$를 곱하고 $y$에 대해 적분해보자.

\[\Rightarrow \int_{a}^{b} L G(x, y)f(y)dy\]

여기서 그린 함수의 정의에 의해 다음과 같이 바꿔 쓸 수 있다.

\[\Rightarrow \int_{a}^{b} \delta(x-y)f(y)dy\]

여기서 디랙 델타 함수의 sifting property에 따라 다음이 성립한다.

\[\int_{a}^{b}\delta(x-y)f(y)dy = f(x)=Lu\]

한편, $L$은 $x$에만 작용하는 선형 연산자이므로 적분 밖으로 뺄 수도 있다.

\[\Rightarrow L\left(\int_{a}^{b} G(x, y)f(y)dy\right)=Lu\]

따라서

\[u(x)=\int_{a}^{b} G(x,y)f(y)dy\]

와 같이 미분방정식의 해를 구할 수 있다는 것을 알 수 있다.

다시 말해, 그린 함수가 해를 구해내는 방식은 선형대수학에서 역행렬을 이용하는 방식과 유사하다.

$Ax=b$라는 문제에서 $x=A^{-1}b$로 표현되듯 $Lu=f$라는 함수해석학의 문제에 대해서 $u=L^{-1}f$와 유사하게 $G$와 $f$을 곱한 것의 적분으로 표현되는 것이다 (미분의 역연산이 적분이기 때문).

예시 문제 1.

그린 함수는 이론적으로만 보면 의미가 어느정도 와닿긴 하지만 실제로 어떻게 미분방정식의 해를 구하는데 사용되는지는 이해하기 어려울 수 있다. 이를 보완하기 위해 예시 문제를 풀어보면서 그린 함수의 의미에 대해 조금 더 생각해보도록 하자.

아래와 같은 미분방정식을 그린 함수를 이용해서 해를 구해보자.

\[\frac{du}{dx}=x\]

여기서 초기 조건을 $u(a)=0$이라고 두고, 우리가 관심을 갖는 $x$의 범위는 $x\in[a,\infty)$라고 생각하자.

예시 문제 1의 풀이

미분계수를 연산자로 생각하면 우리의 미분연산자 $L$은 다음과 같은 것이다.

\[L=\frac{d}{dx}\]

그리고 그린 함수의 정의에 의해 다음과 같은 그린 함수를 생각할 수 있다.

\[LG(x,y)=\delta(x-y)\]

우선 디랙 델타 함수의 성질에 따라 다음과 같이 그린 함수의 형태를 상정할 수 있다.

\[\begin{cases}LG(x,y) = 0 & \text{for }x\lt y \\ LG(x,y)=0 & \text{for }x\gt y\end{cases}\]

즉, $G(x,y)$는 $x\lt y$ 및 $x\gt y$인 구간에서는 미분연산자 $L$의 homogeneous solution을 통해 표현할 수 있게 되는 것이다. 한번 미분해서 0이 되는 경우는 상수함수에 해당한다. 즉,

\[\begin{cases}G(x,y) = c_1 & \text{for }x\lt y \\ G(x,y)=c_2 & \text{for }x \gt y\end{cases}\]

라고 쓸 수 있다.

한편, 그린 함수의 정의를 생각해보면 다음과 같은 사실도 생각해볼 수 있다.

\[\frac{\partial }{\partial x}G(x,y)=\delta(x-y)\]

(여기서 미분연산자 $d/dx$가 $\partial/\partial x$로 바뀐 것은 $G$는 $(x, y)$ 두 변수에 대한 함수이기 때문이다.)

다시 말해 $G(x,y)$는 $x=y$라는 점에서는 불연속적인 값을 갖는 함수일 것이라는 것이다. 거기에, 충분히 작은 양의 실수 $\epsilon$에 대해서

\[\int_{y-\epsilon}^{y+\epsilon}LG(x,y)dx=\int_{y-\epsilon}^{y+\epsilon}\frac{\partial}{\partial x}G(x,y)dx\] \[=G(y+\epsilon,y)-G(y-\epsilon,y)=\int_{y-\epsilon}^{y+\epsilon}\delta(x-y)dx=1\]

이라는 사실을 알 수 있으므로 $x=y$ 값을 기준으로 양 옆의 값이 1만큼 차이나는 함수의 형태를 띄고 있다는 것을 상상해볼 수 있다.

대략적인 그린 함수의 형태는 아래의 그림 7과 같을 것이다.

그림 7을 볼 때는 $x$, $y$의 값이 같을 때 discontinuity가 있다는 것에 주목해야하며 $x$, $y$의 범위는 중요하지 않다. 또, discontinuity가 있는 곳의 함수값의 차이가 1이라는 것에 주목하도록 하자.

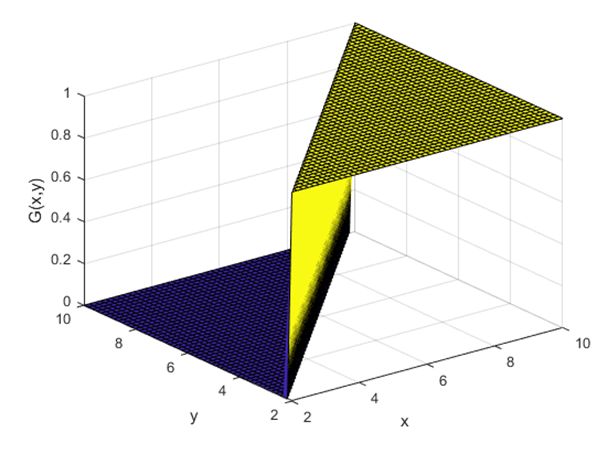
그림 7. 연산자 $L$이 1계 미분계수인 경우의 그린 함수의 대략적인 형태

여기서 초기값 조건을 이용하면

\[G(a,y)=0\]

이므로 식 (35)에서 $c_1=0$이고 $c_2=1$인 것을 알 수 있다. 따라서,

\[G(x,y) = \begin{cases}0 & x\in [a,y) \\ 1 & x \in (y,\infty)\end{cases}\]

와 같이 그린 함수를 계산할 수 있다.

이 함수는 unit step function $H(x)$를 $y$만큼 양의 방향으로 평행이동 시킨 것으로도 볼 수 있다.

여기서 $H(x)$는 다음과 같은 형태이다.

\[H(x)=\begin{cases}1, & x\gt 0\\ 0, & x \lt 0\end{cases}\]

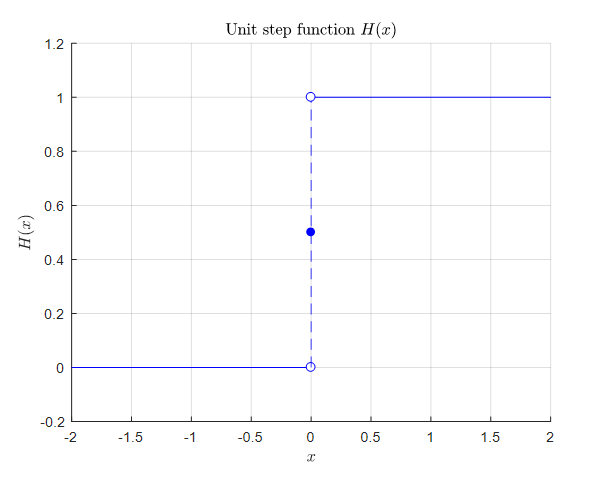
그림 8. unit step function의 형태

그러므로 미분방정식의 솔루션은

\[u(x)=\int_{a}^{\infty}G(x,y)f(y)dy\]

이며, unit step function $H(x)$을 이용해서 쓰면,

\[\Rightarrow \int_{a}^{\infty}H(x-y)f(y)dy\]

이고 $H(x-y)$는 $y$ 관점에서 보면 unit step function을 좌우로 뒤집어 둔 뒤 $x$만큼 양의 방향으로 이동한 것으로 파악할 수 있다.

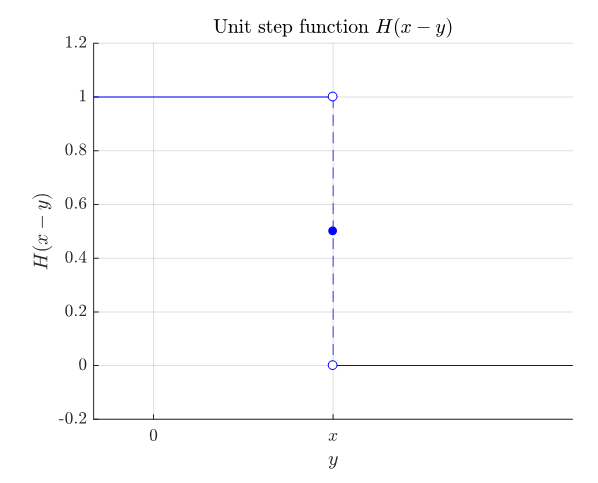
그림 9. unit step function $H(x-y)$의 형태

따라서, 솔루션을 구하면,

\[u(x)=\int_{a}^{x}ydy=\left[\frac{1}{2}y^2\right]_{a}^{x}=\frac{1}{2}x^2-\frac{1}{2}a^2\]

이라는 사실을 알 수 있다.

예시 문제 2.

이번에는 2계 미분계수가 포함되는 미분방정식을 그린 함수를 이용해 풀어보자.

가령, 아래와 같은 미분방정식을 생각해보자.

\[\frac{d^2}{dx^2}u=f(x)\]

여기서 경계조건은 다음과 같이 주어졌다고 생각해보자.

\[u(0)=0, u(\pi)=0\]

예시 문제 2의 풀이

우리에게 주어진 연산자 $L$은

\[L=\frac{d^2}{dx^2}\]

이므로, 그린 함수의 정의에 따라 다음과 같이 그린 함수를 생각할 수 있게 된다.

\[\frac{\partial^2}{\partial x^2}G(x,y)=\delta(x-y)\]

예시 문제 1을 풀 때와 마찬가지로 디랙 델타 함수의 성질을 생각하면 다음과 같은 성질을 만족해야 한다.

\[\begin{cases}LG=0 & \text{for }x\lt y \\ LG=0 & \text{for }x\gt y\end{cases}\]

따라서, $G(x,y)$는 $x\lt y$ 및 $x\gt y$인 구간에서 연산자 $L$의 homogeneous equation을 이용해 표현할 수 있는 것이다.

두 번 미분해서 0이 되려면,

\[G(x,y)=\begin{cases} c_1x+c_2 & x\lt y\\c_3x+c_4 & x\gt y\end{cases}\]

가 되어야 함을 알 수 있고, 경계 조건에 따라,

\[G(0)=c_2=0\]

이고

\[G(\pi)=c_3\pi+c_4=0\]

임을 알 수 있다.

또, 충분히 작은 양의 실수 $\epsilon$에 대해,

\[\int_{y-\epsilon}^{y+\epsilon}LGdx=\int_{y-\epsilon}^{y+\epsilon}\delta(x-y)dx=1\] \[\Rightarrow \int_{y-\epsilon}^{y+\epsilon}\frac{\partial^2}{\partial x^2}G(x,y)dx=\left[\frac{\partial}{\partial x}G(x,y)\right]_{y-\epsilon}^{y+\epsilon}=1\]

임을 알 수 있다. 다시 말해 즉, $y=x$ 근처에서의 미분계수는 1만큼 차이가 나게 된다.

또,

\[G(y+\epsilon,y)-G(y-\epsilon,y)=0\]

이다. 다시 말해 $G(x,y)$는 $y=x$ 근처에서 연속이다.

그 이유는 귀류법을 이용해 설명할 수 있는데, 만약 $G(x,y)$가 $y=x$ 근처에서 불연속이었다면 $G(x,y)$는 $y=x$ 근처에서 unit step function을 통해 모델링 할 수 있는것이 된다. 그런데, unit step function의 1차 미분이 delta function이고 2차 미분은 unit doublet이라고 함수이다. 그런데, 이미 $G(x,y)$의 2계 미분이 디랙 델타 함수라는 것을 토대로 생각해보면 $G(x,y)$는 $y=x$ 근처에서 연속이어야 한다는 것을 알 수 있다.

따라서 위 조건들을 대입해보면,

\[G(y+\epsilon,y)-G(y-\epsilon,y)=c_3y+c_4-c_1y=(c_3-c_1)y+c_4=0\]

이고,

\[G'(y+\epsilon,y)-G'(y-\epsilon,y)=c_3-c_1=1\]

이다. 위 조건들을 조합하면 그린 함수는 다음과 같다는 것을 알 수 있다.

\[G(x,y)=\begin{cases}\left(\dfrac{y}{\pi}-1\right)x, & x\lt y \\\\ \left(\dfrac{x}{\pi}-1\right)y, & x \gt y\end{cases}\]

와 같다.

그린 함수를 $y=\pi/3$ 인 경우에 대해 그려보면 다음과 같은 형태를 띈다는 것을 알 수 있는데,

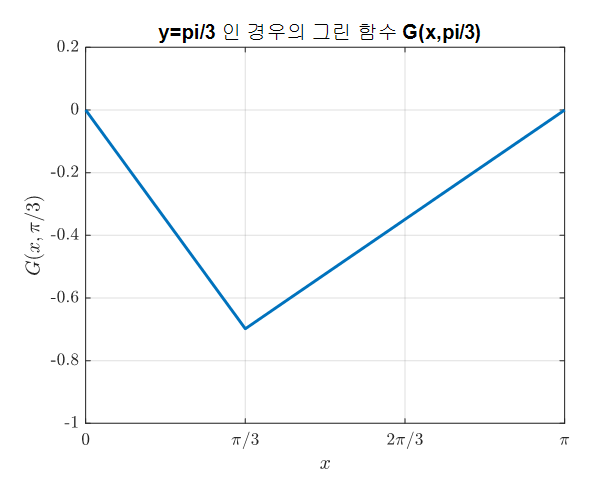
그림 10. 예시 문제 2의 $y=\pi/3$인 경우의 그린 함수

원래의 미분방정식 $u_xx=f(x)$는 파동의 형태에 대한 미분방정식이고, $u(0)=0$, $u(\pi)=0$인 것을 생각해보면 양 끝이 고정되어 있는 로프의 움직임과 관련된 모델을 보여주는 것이라 할 수 있다.

그리고, 그림 10과 같은 그린 함수의 형태가 말해주는 것은 $y=\pi/3$이라는 점에 힘이 주어지고 그 때의 로프의 변형이 어떻게 되는지를 나타내주는 것이라 할 수 있다.

이런 식의 설명이 가능한 이유는 다음의 식을 생각해보았을 때,

\[LG=\delta(x-y)\]

비제차 미분방정식의 의미 편에서 보았던 것 처럼 비제차 항(여기서는 $\delta(x-y)$)은 자체적인 미분방정식 시스템(autonomous system)과는 관계없는 외부로부터 들어오는 forcing term 이기 때문이다.

다시 말해, $\delta(x-y)$는 $x=y$일 때의 외부로부터의 충격에 가까운 입력이다. 따라서 그림 10에서 말하는 것은 $y=\pi/3$인 위치에 외부 충격이 가해지면 그 때의 로프의 상태는 그림 10의 것과 같다라고 해석할 수 있게 되는 것이다.

(여담으로, 이런 식으로 그린 함수를 해석하는 것을 신호/시스템 과목에서는 impulse response라고 부르기도 한다. 물론 Time Invariant 속성이 추가되어야 한다. 다시 말해, impulse response는 그린 함수의 특수 케이스라고도 볼수도 있다.)

만약 $f(x)=x$라고 하면 솔루션은 다음과 같이 얻을 수도 있다.

\[u(x)=\int_{0}^{\pi}f(y)G(x,y)dy=\int_{0}^{x}\left(\frac{x}{\pi}-1\right)y\cdot y ~dy+\int_{x}^{\pi}\left(\frac{y}{\pi}-1\right)x\cdot y~dy\] \[=\frac{1}{6}x^3-\frac{\pi^2}{6}x\]

예시 문제 3.

이번에는 2계 미분방정식의 형태가 조금 더 복잡해진 경우를 보자.

\[\frac{d^2}{dx^2}u+k^2u=f(x)\]

여기서 경계 조건은 다음과 같이 생각해보자.

\[u'(0)=0, u'(l)=0\]

예시 문제 3 풀이

예시 문제 2번의 풀이와 유사하게 $x\lt y$ 인경우와 $x\gt y$ 인 경우로 나눠 풀이할 수 있다.

$x\lt y$ 인 경우에 대해, 미분 연산자 $L$은

\[L=\frac{d^2}{dx^2}+k^2\]

이므로, 이 경우의 그린 함수는

\[\frac{\partial^2}{\partial x^2}G(x,y)+kG(x,y)=0\]

이다.

따라서, 그린 함수는

\[G=A\cos kx+B\sin kx\]

인데, 경계 조건 중 첫번째 조건을 대입하면,

\[G=A\cos kx\]

임을 알 수 있다.

$x\gt y$인 경우에 대해서는 마찬가지 미분연산자를 이용하되 경계 조건 중 두번째를 대입하면

\[G=B\cos k(x-l)\]

임을 알 수 있다.

그린 함수의 $x=y$ 근처에서의 연속 조건과 미분 계수의 차이가 1이라는 조건을 만족시킬 수 있는 그린 함수를 찾으면 다음과 같다.

\[G(x,y)=\begin{cases} \cos(kx)\cos(k(y-l))/(k\sin(kl)) & x \lt y \\ \cos(k(x-l))\cos(ky)/(k \sin(kl)) & x \gt y \end{cases}\]

만약 $k=1$, $l=1$인 경우라고 하면 그린 함수의 형태는 다음과 같다.

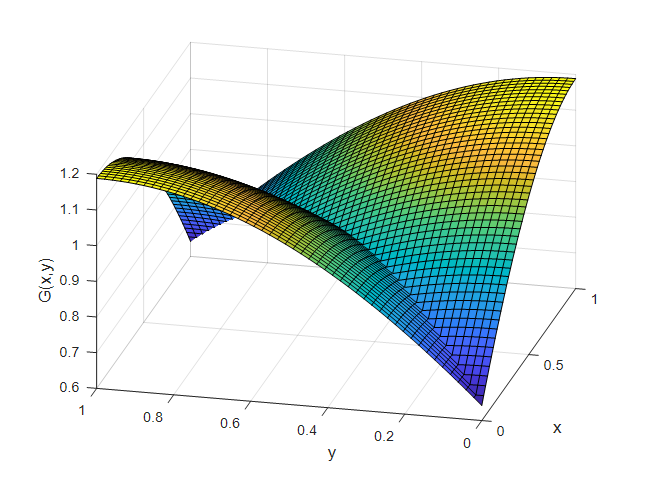
그림 11. 예시 문제 3의 그린 함수

마찬가지 방법으로 $f(x)$가 정해지면 그린 함수와 $f(x)$의 적분을 통해 솔루션 $u(x)$를 구할 수 있게 된다.

참고 문헌

• Advanced Differential Equations: Asymptotics & Perturbations, J. Nathan Kutz, University of Washington
• Green’s function, Wolfram Alpha
• StackEschange: Green function Impulse response confusion
• Brilliant: Green’s Funcions in Physics
• Green’s functions for ODEs, David Skinner, University of Cambridge
• Wikipedia: Green function