임의의 복소수 $x+iy$를 생각해보자.
여기서 $x$와 $y$는 실수라고 하자.
이 값은 극좌표계를 이용해 표현하면 다음과 같이 표현할 수도 있다.
원점에서 $x, y$까지의 거리가 $r$이고 $x$축과 이루는 각도가 $\theta$라고 했을 때,
\[x+iy = r\cos(\theta) + i r\sin(\theta)\]이다.
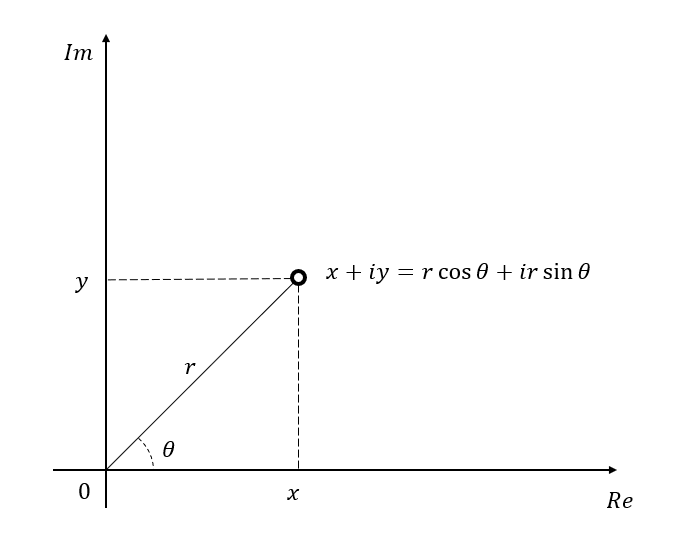
그림 1. 복소평면 상의 점 하나는 복소수 하나를 표현한다.
여기서 $r=1$인 경우를 상정해 이 값을 $z$라고 하도록 하자.
\[z = \cos(\theta) + i \sin(\theta)\]이 $z$라는 값은 반지름이 1인 단위 원 상의 점이 된다.
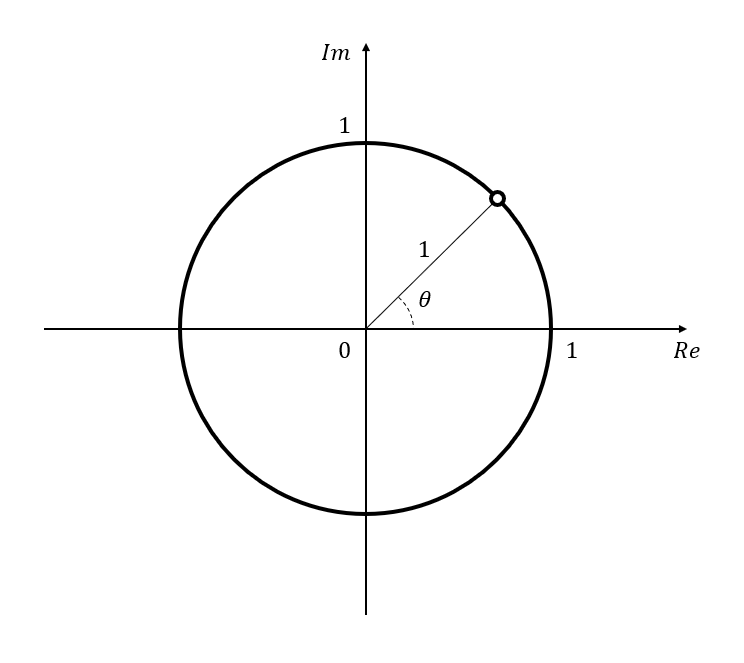
그림 2. 복소평면 상의 단위원 위의 점 $z$. $z$는 $x$축 과의 각도가 $\theta$이다.
여기서 $z$를 $\theta$에 대해 미분해보면 그 값은 다음과 같다.
\[\frac{dz}{d\theta}=-\sin(\theta) + i \cos(\theta)\]여기서 $-i$를 양변에 곱해주자.
그러면,
\[(-i)\frac{dz}{d\theta} = (-i)(-1)\sin(\theta) + (-i)(i)\cos(\theta)\] \[=\cos(\theta) + i\sin(\theta)\]임을 알 수 있다.
그런데 식 (5)는 식 (2)와 같으므로,
\[(-i)\frac{dz}{d\theta}=z\]임을 알 수 있다.
여기서 식 (6)을 약간 변형하여 $z$에 대한 식은 모두 좌변에, $\theta$에 관한 식은 모두 우변에 모아보자.
\[식(6) \Rightarrow \frac{dz}{z}=\frac{1}{(-i)}d\theta\] \[\Rightarrow \frac{dz}{z}=id\theta\]이제 식 (8)의 양변을 적분시켜주면,
\[\int\frac{dz}{z}=\int i d\theta\] \[\Rightarrow \ln(z)=i\theta + C\]여기서 $C$는 적분상수이다.
이 식을 다시 한번 쓰면,
\[z = A_0 e^{i\theta}\]라고 할 수 있다.
여기서 $A_0$는 임의의 상수이다.
이제 $A_0$를 결정해보자.
식 (11)은 식 (2)와 같은 것이므로 다음과 같이 쓸 수 있다.
\[A_0e^{i\theta}=\cos(\theta) + i \sin(\theta)\]여기서 $\theta = 0$인 경우를 생각해보면,
\[A_0 = \cos(0)+i\sin(0) = 1\]임을 알 수 있다.
따라서,
\[e^{i\theta}=\cos(\theta) + i \sin(\theta)\]이다.