prerequisites
그린 정리를 이해하기 위해선 다음의 세 가지 내용에 대해 알고 오시는 것이 좋습니다.
- 미적분학의 기본정리
함수 $f$가 닫힌구간 $[a, b]$에서 연속이며, 함수 $F$가 $f$의 임의의 부정적분이면 다음이 성립한다.
\[\int_{a}^{b}f(t)dt = F(b) - F(a)\]그린 정리
평면에서의 그린 정리는 다음과 같다.
| THEOREM 1. 그린 정리 |
|---|
| 벡터장이 $F(x,y) = P(x,y)\hat{i} + Q(x,y)\hat{j}$로 주어져있고, 선적분의 방향은 면적 A의 boundary에 대해 반 시계 방향이라고 할 때, |
위 식에서 볼 수 있듯이 좌변에는 중적분, 우변에는 선적분의 결과가 있으며 두 결과 값이 같다는 것을 보여주고 있다.
특히, 그린 정리를 생각할 때 중요한 점 중 하나는 닫힌 경로에 대해서 그 경로와 내부 면적에 대해 적용하는 정리(theorem)라는 점이다.
그린 정리의 증명
본 post에서 그린 정리의 증명의 방식은 선적분을 먼저 증명하고, 그 결과가 중적분의 결과와 같다는 것을 보여주는 것이 될 것이다.
증명을 위해 다음과 같은 닫힌 경로를 생각해보자.
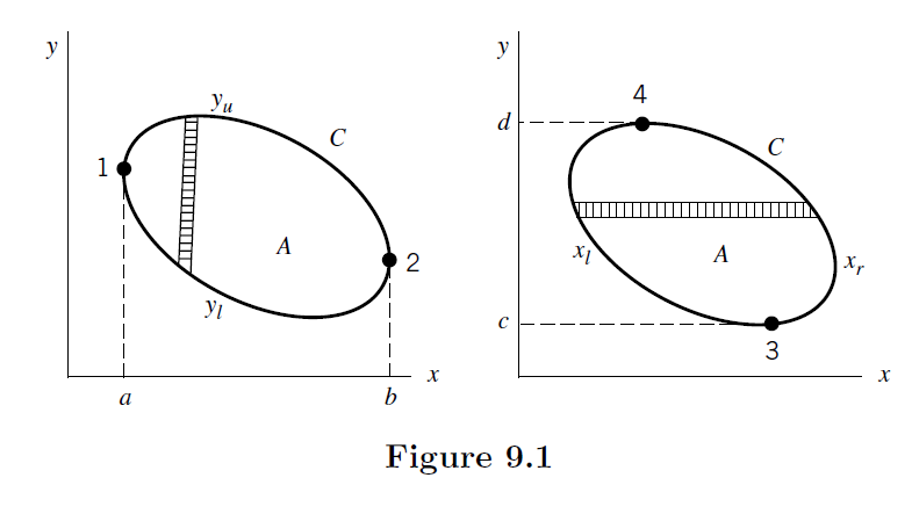
그림 1. 그린 정리 증명을 위해 생각한 닫힌 경로 C와 내부의 면적 A.
출처: Mathematical Methods in the Physical Sciences, pp. 309, 3rd ed., Mary L. Boas
위 그림에서 타원이 두 개가 보이는데 둘 다 같은 닫힌 곡선을 의미하는데 경로만 다르게 설정된 것이다.
그림 1의 왼쪽에서 보면 $x$가 $a$에서 $b$까지 바뀌고 아랫쪽 곡선을 $y_l$, 윗쪽 곡선을 $y_u$라고 명명하였다.
또, 그림 1의 오른쪽에 있는 닫힌 곡선에서는 $y$가 $c$에서 $d$까지 바뀌고, 왼쪽에 있는 곡선을 $y_l$, 오른쪽에 있는 곡선을 $y_r$로 명명하였다.
우리는 이 때 아래와 같은 벡터장이 주어져있다고 생각해보자.
\[\vec{F}(x,y)=P(x,y)\hat{i}+Q(x,y)\hat{j}\]우리는 이제 아래와 같이 선적분을 계산할 수 있다.
\[\oint_C\vec{F}(x,y)d\vec{r} = \oint_C\left(P(x,y)\hat{i}+Q(x,y)\hat{j}\right)(dx\hat{i}+dy\hat{j})\] \[=\oint_C P(x,y)dx + Q(x,y)dy\]한번에 적분식을 계산하기에는 식 (5)가 복잡하기 때문에, 식 (5)의 적분을 계산할 때 $x$ 성분에 대한 결과와 $y$ 성분에 대한 결과를 각각 계산해서 더해주는 방식으로 계산을 진행하자.
$x$ 성분에 대한 적분
그림 1의 왼쪽 타원을 보면 닫힌곡선 C에서 $x$는 $a$에서 $b$까지 바뀌며, 그 때 따라가는 곡선은 $y_l$과 $y_u$로 나눠서 생각해볼 수 있다.
\[\oint_C P(x,y)dx\] \[=\int_{a}^{b}P(x,y_l)dx + \int_{b}^{a}P(x,y_u)dx\]여기서 식(7)의 두 번째 적분식의 $a$, $b$의 순서를 바꿔주고 부호를 반대로 바꿔주자.
\[=\int_{a}^{b}P(x,y_l)dx - \int_{a}^{b}P(x,y_u)dx\] \[=\int_{a}^{b}P(x,y_l) - P(x,y_u)dx\]여기서 미적분학의 기본정리를 사용하면 다음과 같다.
\[=\int_{a}^{b}\int_{y_u}^{y_l}\frac{\partial P}{\partial y}dy\text{ }dx\]여기서 미적분학의 기본정리를 이용했다는 것은 임의의 닫힌구간 $[a,b]$에서 연속이고 미분가능한 함수 $f$에 대해
\[\int_{a}^{b}\frac{df}{dx}dx=f(b)-f(a)\]와 같이 생각할 수 있기 때문이다.
식 (10)에서 $y_l$과 $y_u$의 위치를 바꿔주고 (-) 부호를 붙여주자.
굳이 $y_l$과 $y_u$의 위치를 바꿔주는 것은 그림 1에서 확인할 수 있듯이 $y$축의 증가 방향은 $y_l$에서 $y_u$로 가는 방향이기 때문이다.
\[식(10) \Rightarrow -\int_{a}^{b}\int_{y_l}^{y_u}\frac{\partial P}{\partial y}dydx\] \[=-\iint_A\frac{\partial P}{\partial y}dxdy\](푸비니의 정리로 중적분 시 $dx$와 $dy$의 순서가 바뀌어도 상관이 없다.)
$y$ 성분에 대한 적분
이번엔 $y$성분에 대한 적분을 해보도록 하자.
그림 1의 오른쪽 타원을 보면 닫힌곡선 C에서 $y$는 $c$에서 $d$까지 바뀌며, 그 때 따라가는 곡선은 $x_l$과 $x_r$로 나눠서 생각해볼 수 있다.
\[\oint_CQ(x,y)dy\] \[=\int_{d}^{c}Q(x_l, y)dy + \int_c^dQ(x_r,y)dy\]마찬가지 방법으로 식 (15)의 왼쪽 적분식의 $c$와 $d$의 순서를 바꾸고 부호를 바꿔주자.
\[=-\int_{c}^{d}Q(x_l, y)dy + \int_c^dQ(x_r,y)dy\] \[=\int_c^d Q(x_r,y)-Q(x_l,y)dy\]$x$ 성분에 대한 적분을 해줄때와 마찬가지로 미적분학의 기본정리를 이용하면,
\[=\int_c^d \int_{x_l} ^{x_r} \frac{\partial Q}{\partial x}dx dy\] \[=\iint_A\frac{\partial Q}{\partial x}dxdy\]x, y 성분에 대해 계산한 결과들을 합해주자.
원래 그린정리에서 구하려고 했던 값들을 생각해보면 앞서 구한 x, y 성분에 대한 선적분 값들을 합쳐준 것이다.
즉,
\[식(5) = -\iint_A\frac{\partial P}{\partial y}dxdy + \iint_A\frac{\partial Q}{\partial x}dxdy\] \[= \iint_A\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}dxdy\]이다.
이로써 그린 정리를 증명할 수 있다.
Curl을 통한 그린 정리의 직관적 이해
아래의 내용을 이해하기 위해선 아래의 내용을 알고 오시는 것이 좋습니다.
이번에는 그린정리의 직관적인 의미를 좀 더 이해해보도록 하자.
다음과 같이 어떤 벡터장 위에 넓이를 갖는 영역 R이 있다고 하자.
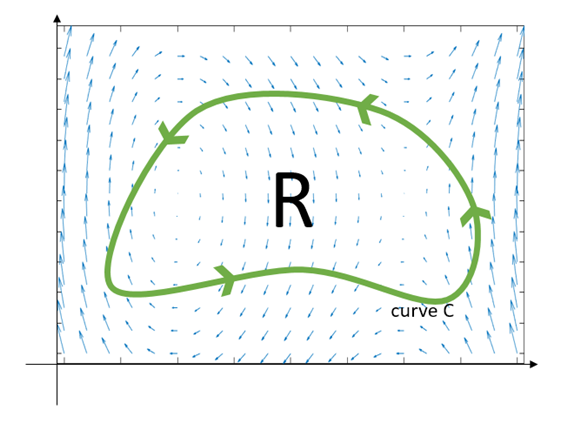
그림 2 xy 평면 위에 임의의 벡터장 $f$와 폐곡선 C가 있다.
벡터장 $\vec{f}$를
\[\vec{f}(x,y) = P(x,y)\hat{i}+Q(x,y)\hat{j}\]라고 하면, 그린 정리에 의해 다음이 성립한다.
\[\oint_C\vec{f}\cdot d\vec{r} = \iint_R\left(\frac{\partial P}{\partial y}-\frac{\partial Q}{\partial x}\right)dA\]식 (23)의 좌변은 curve C를 따라 벡터장 에 대해 선적분 한 것이다.
선적분 값은 curve를 따라 벡터장이 curve를 따라 CCW로 흐르면 양의 값이 나올 것이고 curve를 따라 벡터장이 대부분 CW로 흐르면 음의 값이 나온다.
이제 식 (23)의 좌변으로부터 식 (23)의 우변을 유도해보자. 영역 R을 아래와 같이 반으로 쪼개서 보도록 하자.
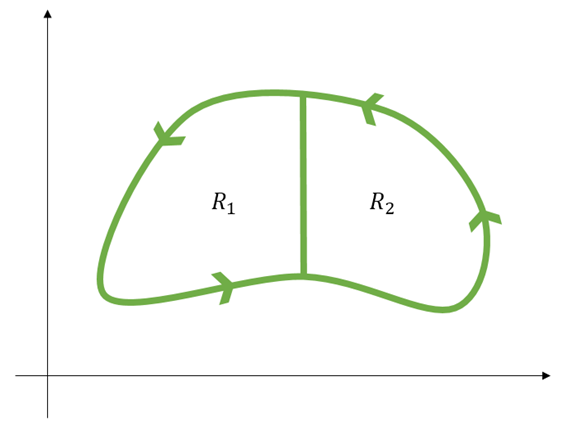
그림 3 영역 R을 이등분 해보자. 세로로 쪼개든 가로로 쪼개든 어떻게 쪼개도 상관없다.
그럼 $R_1$영역의 폐곡선을 $C_1$, $R_2$영역의 폐곡선을 $C_2$라고 해보자. 그러면 다음이 성립한다.
\[\oint_{C_1}\vec{f}\cdot d\vec{r} + \oint_{C_2}\vec{f}\cdot d\vec{r} = \oint_{C}\vec{f}\cdot d\vec{r}\]왜 그런가? $R_1$과 $R_2$사이의 boundary 에서는 $C_1$에서 구하게 되는 선적분과 $C_2$에서 구하게 되는 선적분의 값이 상쇄되기 때문이다.
그것은 선적분은 기본적으로 벡터장이 얼마나 CCW 방향으로 닮았는지 확인하는 것이기 때문이다.
이제 $R$을 아래와 같이 사등분 해보자.
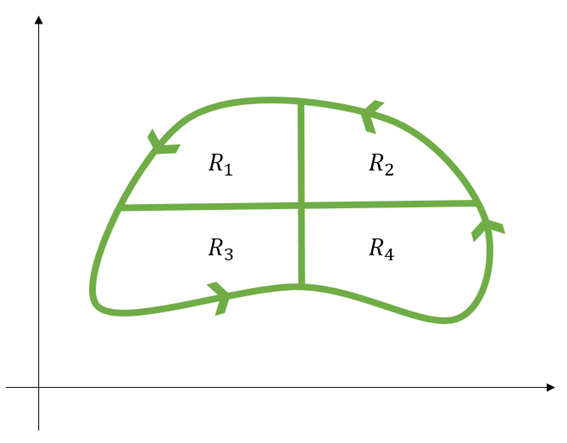
그림 4 영역 R을 4등분했다. 어떤 모양으로 쪼개든지 큰 상관은 없다만 편하게 생각하기 위해 위와 같이 쪼개보자.
앞에서와 같은 논리로 다음이 성립한다.
\[\oint_{C_1}\vec{f}\cdot d\vec{r} + \oint_{C_2}\vec{f}\cdot d\vec{r} + \oint_{C_3}\vec{f}\cdot d\vec{r} + \oint_{C_4}\vec{f}\cdot d\vec{r} = \oint_{C}\vec{f}\cdot d\vec{r}\]–
그렇다면 영역 R을 N등분하면 어떻게 될까? 다음의 식을 성립시킬 수 있다.
\[\sum_{k=1}^{N}\oint_{C_k}\vec{f}\cdot d\vec{r} = \oint_{C}\vec{f}\cdot d\vec{r}\]이제 식 (26)에 대해 고민해보기 위해 영역 $R$을 N 개로 쪼갰을 때, 임의의 $k$ 번째 영역에 대해 잠시 고려해보자.
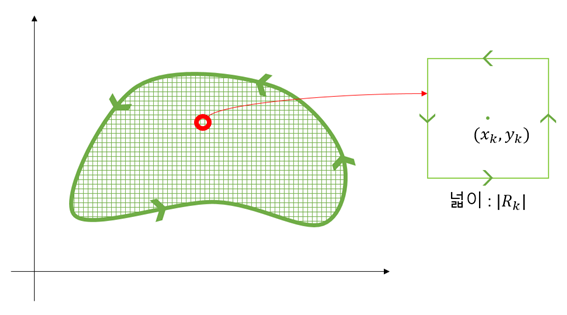
그림 5 영역 R을 N개로 나누었다고 했을 때 k 번째 영역 $R_k$.
Curl 편에서 확인했듯이 curl은 단위 영역이 받는 회전력이다.
그렇다면 $N\rightarrow \infty$일 때 이 $R_k$영역은 미소 영역으로 생각할 수 있을 것이다.
그러면 넓이가 $|R_k|$인 영역 $R_k$의 회전량은 얼마인가?
그것은
\[\text{2d-curl}\left\{F(x_k,y_k)\right\}|R_k|\]가 된다.
즉, 이것은
\[\oint_{C_k}\vec{f}\cdot d\vec{r}\]과 같은 의미를 갖는다. 왜냐하면 회전에 관여하는 벡터만 고려하여 선적분 해주는 것이 curl을 생각하는 방법이었기 때문이다.
(바로 이해되지 않는다면 벡터장의 회전(curl) 편을 보기를 강력 추천한다.)
따라서 식 (26)은 다음과 같이 고려해줄 수 있다.
\[\Rightarrow \oint_C\vec{f}\cdot d\vec{r}=\sum_{k=1}^{N}\oint_{C_k}\vec{f}\cdot d\vec{r}\approx \sum_{k=1}^{N}\text{2d-curl}\left\{F(x_k, y_k)\right\}|R_k|\]이 때 $N$을 무한하게 크게 만들면 $|R_k|\rightarrow dA$가 되고,
따라서,
\[\oint_C\vec{f}\cdot d\vec{r} = \iint_R\text{2d-curl}\left\{\vec{f}\right\}dA = \iint_R\left(\frac{\partial P}{\partial y} - \frac{\partial Q}{\partial x}\right)dA\]가 된다.