편미분

우리는 이제 multivariate calculus로 들어가고자 한다.

지금까지는 독립변수 하나에 종속 변수가 하나인 함수에 대해서 미분을 해왔지만, multivariate calculus에서는 독립변수가 여러개에 종속변수도 여러 개일 수 있다.

우선은 독립 변수가 2개이고 종속 변수가 하나인 가장 단순한 형태까지만 확장한 multivariate function을 보도록 하자.

쉬운 예로 다음과 같은 함수를 생각할 수 있다.

\[f(x,y) = x^2+xy+y^2\]

이 함수를 MATLAB을 이용해 plot하면 다음과 같이 그릴 수 있다.

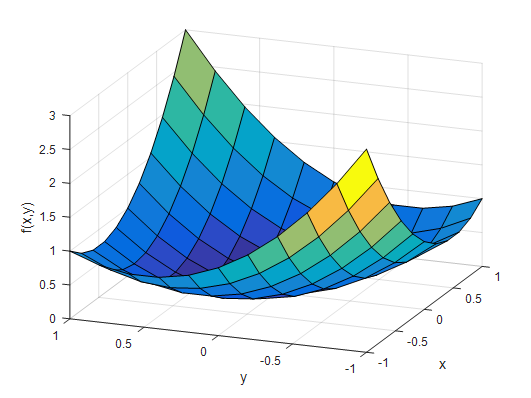
그림 1. f(x,y) = x^2 + xy + y^2 을 도시한 것.

함수에서 미분의 개념은 기울기를 의미한다.

그런데 우리가 지금까지 알고 있는 기울기를 위의 함수에서 바로 구할 수 있을까? 임의의 점 하나를 찍어 보면 그 점에서 기울기 직선은 하나로 유일하게 결정되지 않는다는 것을 알 수 있다.

편미분이라는 개념이 필요한 이유는 이러한 상황에서 수직인 두 방향으로만 기울기를 구하고 싶다는 이유에서 출발한다고 할 수 있다.

즉, $f(x,y)$의 $x$방향 만으로의 기울기와 $y$방향 만으로의 기울기는 각각 구할 수 는 있기 때문에 $y$ 또는 $x$를 상수로 놓고 미분함으로써 $x$ 방향 만으로의 기울기와 $y$ 방향 만으로의 기울기를 구하는 것이다.

기호로써 함수 $f$의 $x$방향으로의 편미분은 다음과 같은 기호로 쓸 수 있다.

$f_x$ 또는 $\frac{\partial f}{\partial x}$

y의 경우도 마찬가지로

$f_y$ 또는 $\frac{\partial f}{\partial y}$

는 함수 $f$의 $y$방향으로의 편미분을 나타낸다.

Gradient (기울기)

gradient는 $x$ 방향으로의 편미분 값과 $y$ 방향으로의 편미분 값을 원소로 하는 벡터를 출력한다.

조금 복잡하게 들릴 수도 있지만 다음과 같이 수식으로 쓰면 이해가 쉽다.

\[gradient(f) = f_x\hat{i}+f_y\hat{j} = \frac{\partial}{\partial x}f(x,y)\hat{i} + \frac{\partial}{\partial y}f(x,y) \hat{j}\]

위의 $gradient(\cdot)$ 을 다음과 같이 Del (또는 nabla) 연산자를 이용해 쓰기도 한다.

기호일 뿐이니 너무 걱정하지는 말자.

\[\nabla f=f_x\hat{i} + f_y\hat{j} = \frac{\partial}{\partial x}f(x,y) \hat{i} + \frac{\partial}{\partial y}f(x,y)\hat{j}\]

여기 까지 봤을 때, gradient는 어떤 일을 하는가? scalar로 표현되어 있는 함수에서 어떤 벡터 값을 얻어내게 만든다. 즉 입력은 스칼라인데 출력은 벡터가 나오게 되었다.

조금 더 들어가보자.$\nabla f$ 의 우항에 있는 $\frac{\partial}{\partial x}f(x,y)$와 $\frac{\partial}{\partial y}f(x,y)$를 구해보도록 하자.

\[\frac{\partial}{\partial x}f(x,y) = \frac{\partial}{\partial x}(x^2+xy+y^2) = 2x+y\] \[\frac{\partial}{\partial y}f(x,y) = \frac{\partial}{\partial y}(x^2+xy+y^2) = 2y+x\]

그러면 $\nabla f$는 $x, y$의 함수이며 모든 $x, y$ 좌표에 대응되는 벡터가 생성된다는 것을 알 수 있다. 다른 말로 하면 gradient는 스칼라 함수로부터 벡터장을 형성하는 연산자이다.

Scalar 평면에서의 gradient

MATLAB을 통해 gradient가 어떻게 생겼나 확인해보도록 하자.

gradient의 출력은 벡터이기 때문에 $x$ 방향으로의 벡터 element부터 확인해보자.

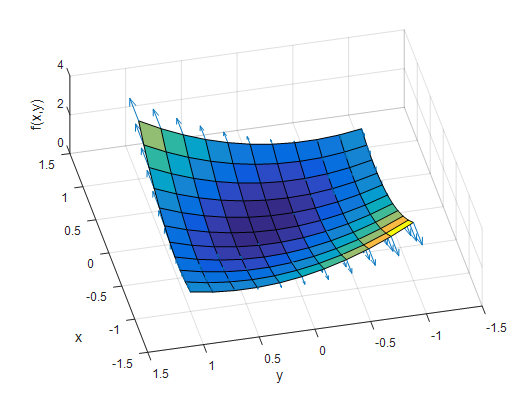
그림 2. gradient의 x 축 방향으로의 성분만 표시한 그림

그림2는 같은 $f(x,y)$를 위에서 바라본 그림이다. 각각의 화살표는 gradient의 x 성분만을 의미한다.

그림에서 볼 수 있듯이 x 축 방향으로의 크기만 바뀌는 것을 볼 수 있는데 각각의 x 성분은 모두 x 방향으로의 기울기를 뜻한다.

이번엔 y 방향으로의 벡터 element를 확인해보자.

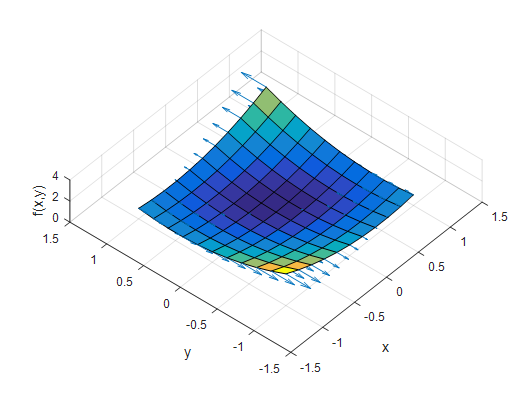
그림 3. gradient의 y 축 방향으로의 성분만 표시한 그림

위 그림을 잘 보면 y 축 방향으로만 크기가 바뀌는 벡터가 모든 $x, y$점에서 생성된 것을 알 수 있다. 이 때 각각의 벡터의 크기는 $y$축 방향으로의 기울기를 의미한다.

그렇다면 $x$ 방향의 벡터 element와 $y$방향의 벡터 element를 모두 한번에 그려주게 되면 어떻게 될까?

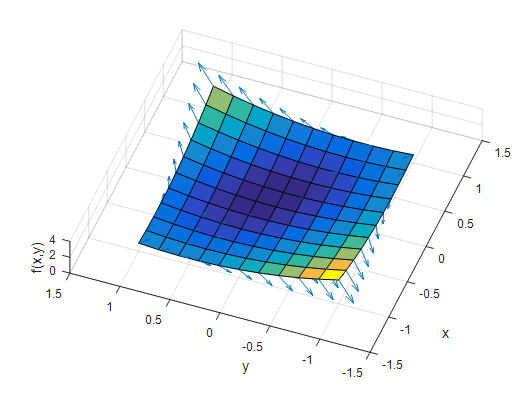
그림 4. gradient의 x축 성분과 y축 성분이 합쳐진 전체 벡터를 표시한 그림

그렇다면 그림 4에서 볼 수 있는 각각의 벡터들은 어떤 것을 의미할까?

그것은 해당 point에서 $f(x,y)$ 평면의 기울기가 가장 가파른 곳으로의 방향을 의미한다.

Scalar field에서의 gradient

Scalar field는 $f(x,y,z)$로 나타낼 수 있다.

Scalar field의 가장 좋은 예로써 온도의 분포를 생각할 수 있다. 방 안의 모든 3차원 좌표를 생각할 수 있으며 그 각각의 좌표에 해당하는 온도를 하나 하나 매핑할 수 있을 것이다.

가령, 3차원 공간안에서 온도가 다음과 같이 정의되었다고 생각해보자.

\[T(x,y,z) = 20\times \exp\left(-(x^2+y^2+z^2)\right)\]

그렇다면 이 $T$라는 스칼라 함수에 대해서 gradient를 구하면 다음과 같다.

\[\nabla T = T_x\hat{i}+T_y\hat{j}+T_z\hat{k}\] \[=20\times \exp \left(-(x^2+y^2+z^2)\right)(-2x\hat{i} - 2y\hat{j} - 2z\hat{k})\]

그렇다면 스칼라 필드 $T(x,y,z)$는 어떤 모양일까? MATLAB으로 그려보면 다음과 같다.

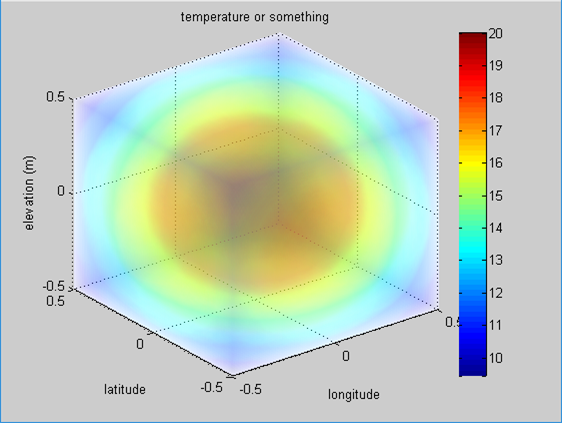
그림 5. 온도 T의 스칼라 필드를 표현한 그림

그러니까 색깔이 빨간색에 가까울수록 온도가 뜨겁다는 것을 의미한다.

그렇다면 이 스칼라 필드에서의 gradient는 무엇을 의미할까?

그것은 임의의 점 $(x,y,z)$에서 온도의 변화가 가장 큰 방향을 의미한다.

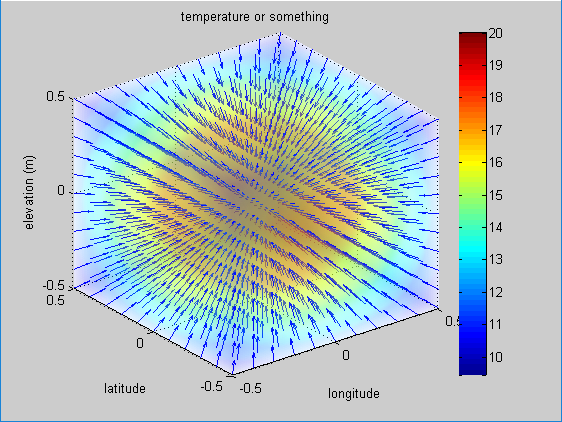
그림 6. 온도 T의 스칼라 필드를 표현한 그림

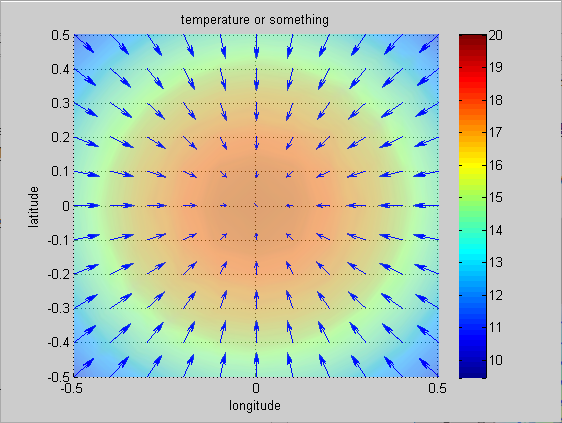
그림 7. 그림 6의 gradient를 위쪽 (view([0 90])에서 본 그림

※ 매트랩 코드는 아래의 제 깃허브 repo에서 받으실 수 있습니다.

$\Rightarrow$ 공돌이의 수학정리노트 Github repo 링크