연속 시간 컨볼루션이 말하는 것: 연속함수는 잘게 쪼개서 표현될 수 있다.

Prerequisites

이 포스팅에 대해 더 잘알기 위해서는 다음의 내용에 대해 알고 오시는 것이 좋습니다.

• 선형 시불변(LTI) 시스템
• 이산 컨볼루션과 임펄스 응답

1. 이산 신호 컨볼루션의 의미 [복습]

이번 시간에는 연속 시간 도메인에서 컨볼루션에 대해 생각해보고자 한다. 우리가 수학을 배울 때 연속 시간 신호(즉, 실수 함수)에 대해 먼저 배우고 대학에 와서야 이산 신호에 대해 배우지만, 사실 이해를 돕기위해서는 이산 시간 도메인에서 개념을 먼저 생각해본 뒤 연속 시간 신호의 관점으로 확장시키는 것이 도움이 되는 경우가 많다.

이산 시간에서 convolution이 의미하는 것은 임의의 함수 $x[n]$ 를 델타 함수 $\delta [n]$ 를 이용해 분해해서 생각할 수 있다는 것이었다. 식으로 쓰자면,

\[x[n]=\cdots + x[-2]\delta[n+2]+x[-1]\delta[n+1]+x[0]\delta[n]+x[1]\delta[n-1]+x[2]\delta[n-2]+\cdots \notag\] \[= \sum_{k=-\infty}^{\infty}x[k]\delta[n-k] = \sum_{k=-\infty}^{\infty}x[n-k]\delta[k]\]

그러니까, 식 (1)은 조금 자세히 보면 함수 $x[n]$ 을 “함수 값 $\times \delta[n]$” 으로 나타낼 수 있다는 걸 알 수 있다. 그렇다면 연속 시간 신호도 함수값과 delta 함수를 이용하면 임의의 신호 $x(t)$ 를 분해할 수 있지 않을까?

이산 신호는 경우에 따라 연속 신호를 sampling한 것으로 볼 수 있다. 이산 신호의 컨볼루션 개념에서부터 연속 신호 컨볼루션의 개념을 이해하고자 한다면 그 연결고리는 sampling에서 찾을 수 있을 것이다. 따라서, 연속신호의 간단한 샘플링 방법에 대해 소개하고자 한다.

2. CT signal의 샘플링 방법: Sample and Hold

연속 신호 시간 신호를 sampling 하는 방법 중 가장 간단한 방법 중 하나는 sample and hold이다. Sample and hold는 아날로그 신호를 측정한 뒤 한 주기 동안 유지하는 방법이다. 특별히 이번 post에서는 0차 sample and hold에 대해서만 간략히 소개하고자 한다.

아래 그림에서 회색으로 표현된 신호는 원래 신호이며, 빨간색 선으로 나타낸 신호는 0차 sample and hold를 이용해 sampling한 신호이다.

그림 1. 0차 sample and hold

0차 sample and order는 매우 간단하다. 특정 시간에 신호의 값을 측정(혹은 획득)하고 다음 측정 주기까지 그 신호 값을 유지시키는 방식이다. 이번 post에서는 0차 sample and hold와 비슷한 방식으로 rect함수를 이용해 연속 신호를 sampling하고자 한다. 위의 Wikipedia의 그림과 달라지는 점은 본 포스트의 가장 상단에서 보이는 것 처럼 sample된 연속 신호의 값이 사각 펄스 왼쪽 상단이 아닌 사각 펄스 중앙에 위치한다는 것이다. (아래 그림의 빨간 화살표)

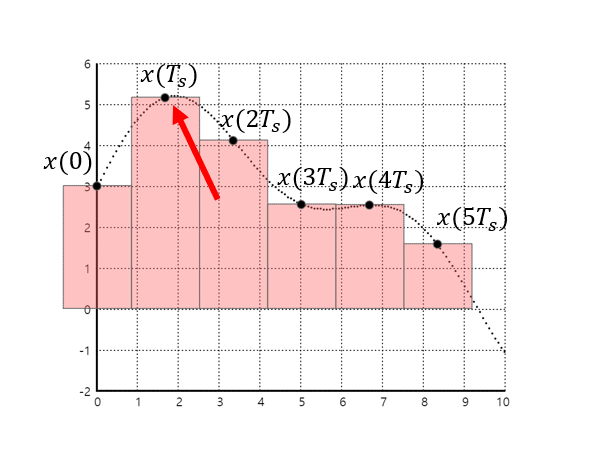
그림 2. 사각파를 이용한 연속신호 sampling

3. sampled signal의 수학적 표현

아래 그림에서 등호 좌측의 그래프는 연속 신호를 주기 $T_s$에 맞추어 sampling한 신호를 표현하고 있다. 그리고 등호 우측의 그래프들은 등호 좌측의 신호는 각각의 sample된 신호들을 합쳐놓은 것으로 생각할 수 있다는 것을 말해주고 있다.

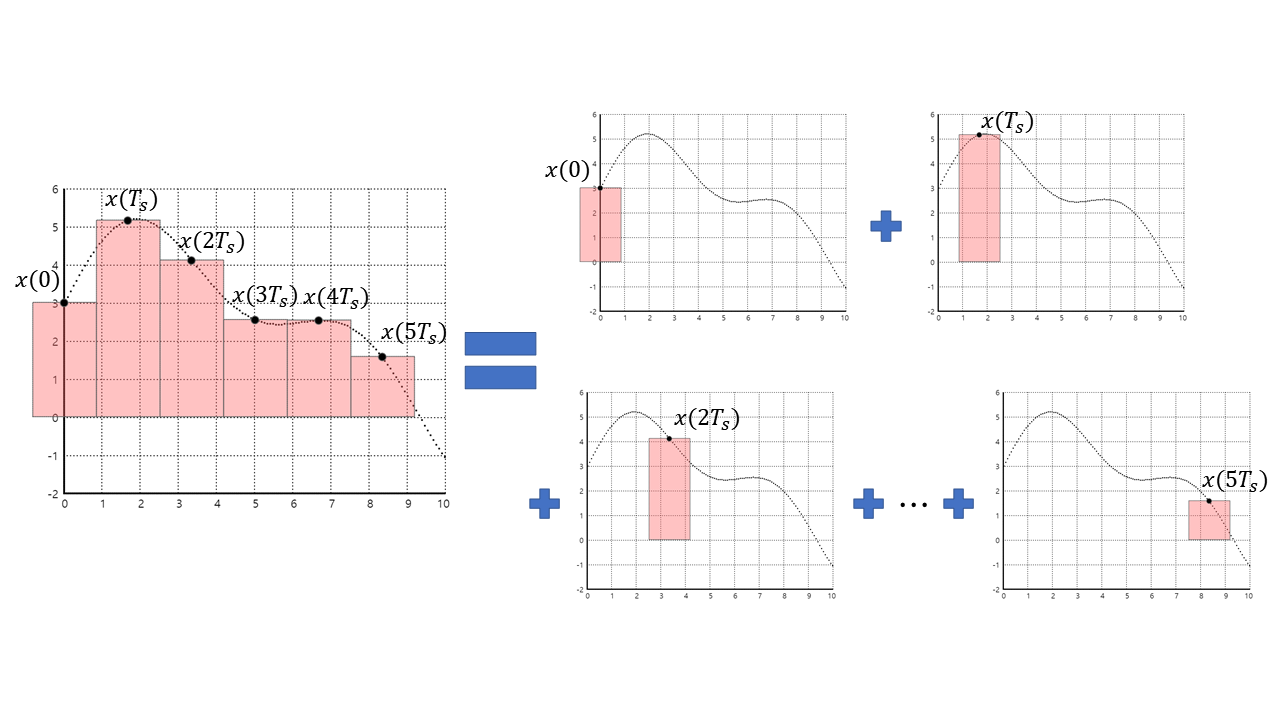
그림 3. sample된 신호는 각 sample 만큼의 크기를 가지고 sample의 위치로 평행이동한 사각파들의 합으로도 볼 수 있다.

위 그림의 등호 우측에 있는 하나 하나의 빨간색 네모들은 수학적으로는 사각파로 표현할 수 있다.

DEFINITION 1. 사각파
사각파 $\Pi(t)$ 는 다음과 같이 정의한다. $$\Pi(t) = \left\{ \begin{matrix} 1, & -0.5\leq t \leq 0.5\\ 0, & otherwise. \end{matrix} \right . $$

그림 4. 사각파의 형태

사각파를 a만큼 평행이동하고, b만큼 늘려준 파형은 다음과 같다.

\[\Pi\left(\frac{t-a}{b}\right)\]

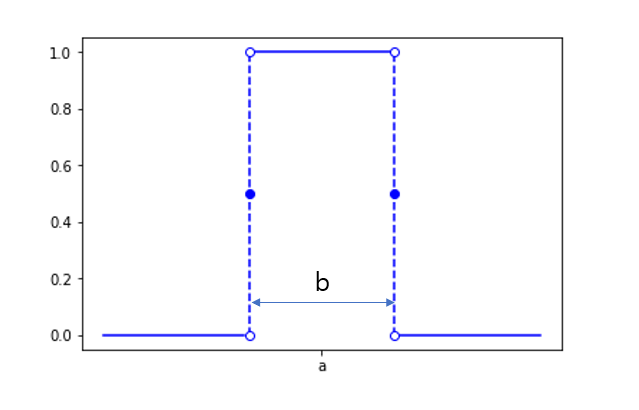
그림 5. 평행이동 및 scaling한 사각파

사각파의 정의를 이용해 그림 3에서 $x(t)$ 를 샘플링한 신호는 다음과 같이 표현할 수 있다.

\[x(t) \rightarrow (샘플링) \rightarrow \sum_{k=-\infty}^{\infty}{x(k T_s) \frac{1}{T_s} \Pi\left(\frac{t-kT_s}{T_s}\right)}\]

위 식에서 $1/T_s$가 들어간 것은 sampling period $T_s$의 길이에 따른 결과의 변화를 방지해주고자 normalize하고자 하는 이유에서이다.

4. 연속신호 컨볼루션

연속신호를 sampling한 신호에서 sampling 주기를 매우 짧게 만들면 다시 연속신호로 완벽히 복원할 수 있다.

따라서, 아래의 식과 같이 $T_s$ 에 극한을 취해줄 수 있다.

\[\lim_{T_s\rightarrow 0}\left\{\sum_{k=-\infty}^{\infty}{x(k T_s) \frac{1}{T_s} \Pi\left(\frac{t-kT_s}{T_s}\right)}\right\}\]

위 식에서 나타내는 과정이 이 포스트 맨 위의 애플릿에서 슬라이드를 오른쪽으로 움직였을 때 표현되어 있다.

그렇다면, 위 식에서 $T_s$ 가 매우 작아질 때 $x(kT_s)$ 부분은 함수 값들을 의미한다는 것을 알겠지만 $\frac{1}{T_s} \Pi(\frac{t-kT_s}{T_s})$ 부분은 델타 함수를 정의함으로써 이해할 수 있을 것이다.

DEFINITION 2. 연속시간 델타 함수
디렉 델타 함수를 표현할 수 있는 방법 중 하나는 다음과 같다. $$\delta(t) = \lim_{h\rightarrow 0^+}\frac{1}{h}\Pi\left(\frac{t}{h}\right)$$

따라서 식 (5)는 정적분의 정의와 델타 함수의 정의에 의해 다음과 같이 쓸 수 있다.

\[\lim_{T_s\rightarrow 0}\left\{\sum_{k=-\infty}^{\infty}{x(k T_s) \frac{1}{T_s} \Pi\left(\frac{t-kT_s}{T_s}\right)}\right\} = \int_{-\infty}^{\infty}{x(k) \delta(t-k)dk}\]

신호 이론에서는 보통 k 대신에 $\tau$ 를 종종 사용한다.

5. 연속 시간 도메인의 impulse response

DT Signal에서와 마찬가지로 LTI(Linear Time Invariant) system의 성질을 이용하면,

입출력의 관계를 linear operator $O$로 나타낼 수 있다고 하자.

\[y(t) = O_n\{x(t)\}\]

그렇다면, 앞서 확인한 연속신호 컨볼루션의 정의에 의해

\[= O_n\left\lbrace\int_{-\infty}^{\infty}{x(k) \delta(t-k)dk}\right\rbrace\]

LTI system의 성질에 의해,

\[=\int_{-\infty}^{\infty}{x(k) O_n\{\delta(t-k)\}dk}\]

다시 impulse response의 정의에 의해서

\[=\int_{-\infty}^{\infty}{x(k) h(t-k)}\]

와 같이 확인할 수 있다.

일반적으로 $k$ 대신에 많이 사용하는 $\tau$ 를 이용해 입력, 출력, impulse response의 관계를 적자면,

\[y(t) = \int_{-\infty}^{\infty}{x(\tau)h(t-\tau) d\tau}\]

라는 사실을 알 수 있다 ¹.