flux는 2차원 발산정리에서 그대로 사용되기 때문에 flux에 대해 이해하는 것은 중요하다고 할 수 있다.
flux는 다음과 같이 수학적으로 기술할 수 있다.
\[\int_C\vec{F}\cdot\hat{n}ds\]또는 아래와 같이 닫힌 경로에 대해서도 flux를 기술할 수 있다.
\[\oint_C\vec{F}\cdot\hat{n}ds\]prerequisites
flux에 대해 이해하려면 다음의 내용에 대해 알고오는 것이 좋다고 생각함.
2D flux
flux가 의미하는 것은 다음과 같다.
“단위 시간 당 경로를 따라 빠져나간 (혹은 들어간) 유량이 얼마인가?”
아래 그림 1과 같이 벡터장이 주어져있다고 할 때 두 개의 경로를 생각해보자.
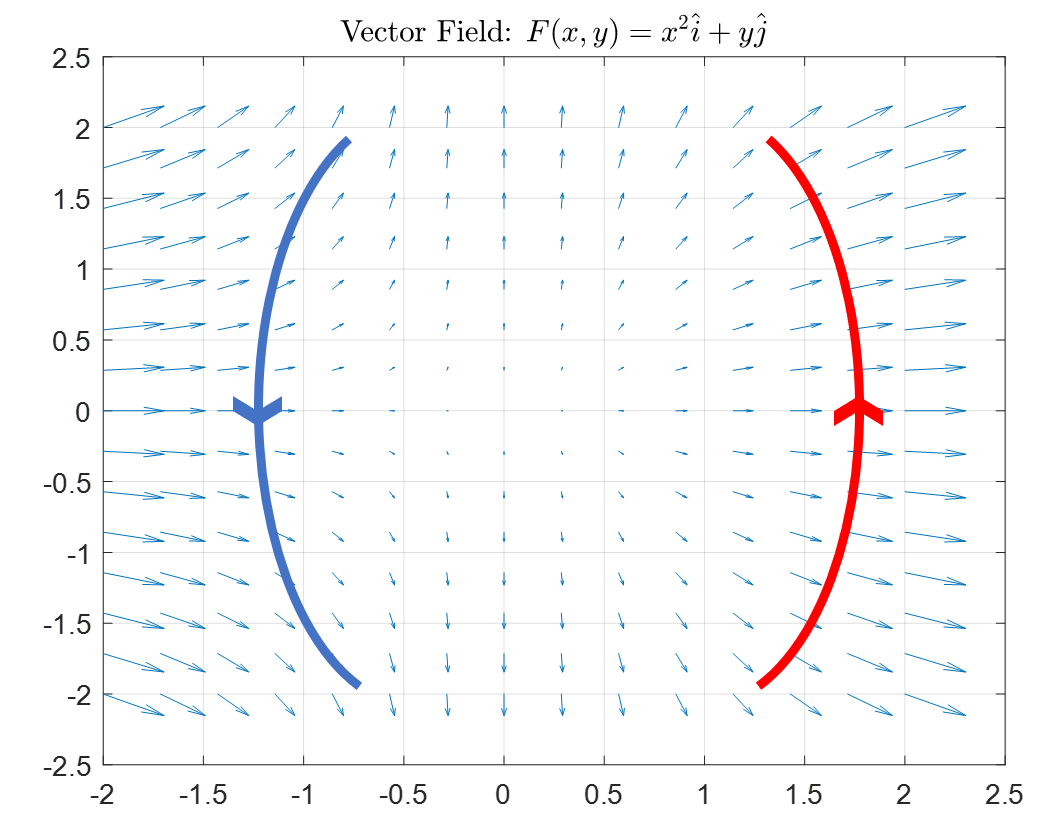
그림 1. 주어진 벡터장 F와 두 개의 임의의 경로 (빨간색 선과 파란색 선). 각 경로는 방향이 주어져 있음.
그림 1에서 주어진 벡터장을 물의 흐름이라고 생각해보면 여기서 flux는 벡터의 방향을 고려해보았을 때 빨간색 혹은 파란색 경로를 따라 빠져나가거나 들어간 물의 총 양을 의미한다고 할 수 있다.
또, flux는 아래와 같이 닫힌 경로에 대해서도 생각할 수 있다.
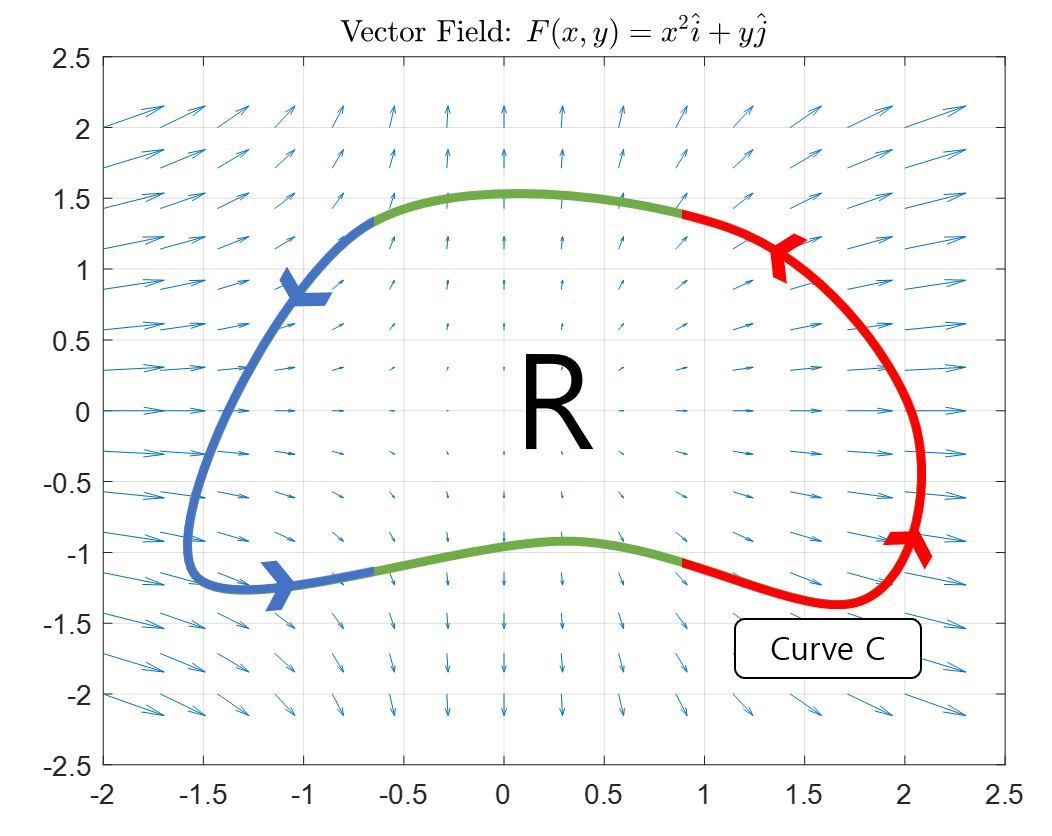
그림 2. 주어진 벡터장 F와 임의의 닫힌 경로. 해당 경로는 방향이 주어져 있음.
그림 1에서와 마찬가지로 그림 2의 닫힌 경로에서도 전체 경로에 대해 flux를 계산할 수 있으며, 빨간색으로 표시된 부분은 빠져나가는 유량이 계산될 것이고 파란색으로 표시된 부분은 들어온 유량이 계산될 것이다.
여기서 잠깐 flux와 벡터장의 발산에 대해 헷갈릴 수도 있는데, 짧게나마 설명을 하자면 벡터장의 발산은 공간 상의 아주 작은 미소 영역에서 빠져나가거나 들어온 유량을 의미하는 것이고, 2D flux의 경우에는 좀 더 macro한 level에서 경로를 따라 빠져나가거나 들어오는 유량을 의미한다.
2D flux의 식 유도
2D flux의 식을 유도하기 위해서 우리는 미소 경로에 대한 flux를 확인한 후 전체 경로에 대해서 적분해줌으로써 2D flux의 식을 유도해 볼 것이다.
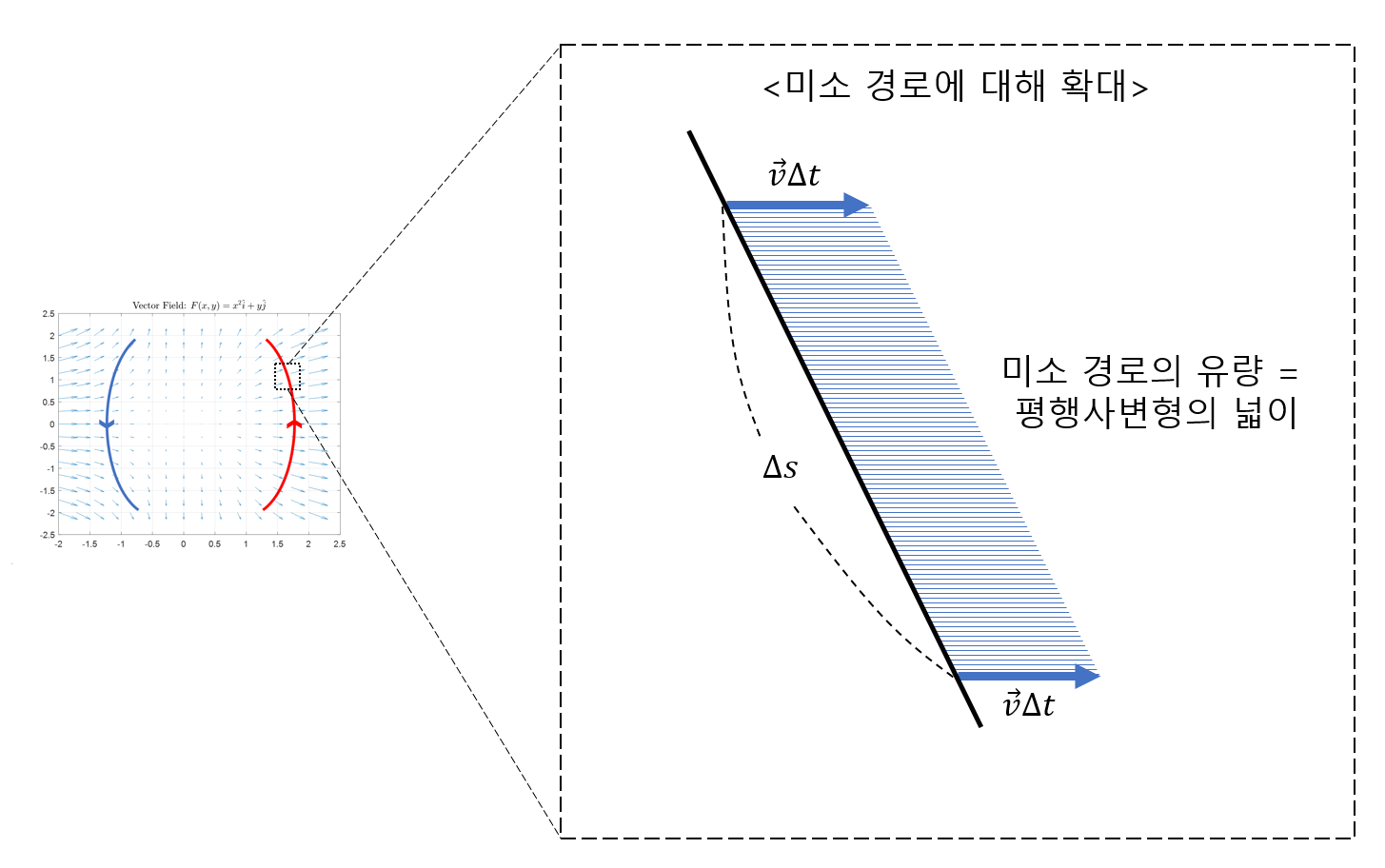
그림 3. 미소 경로에 대한 유량. 벡터 v를 물의 유속으로 생각하고, Δt 만큼의 시간이 지났다고 하면 평행사변형의 넓이가 미소 경로를 통해 빠져나간 물의 양을 유량이라 생각할 수 있다.
그림 3에서 볼 수 있듯이 미소 경로에 대한 유량은 평행사변형의 넓이를 계산해줌으로써 얻을 수 있게 된다. 벡터 $\vec{v}$를 물의 유속이라고 생각하고 $\Delta t$만큼의 시간동안 이 물이 흘렀다고 하면 미소경로를 통해 빠져나간 평행사변형의 넓이를 계산해줌으로써 물이 나간 유량을 계산할 수 있다.
평행사변형의 넓이는 밑변 $\times$ 높이인데, 밑변의 길이는 $\Delta s$라고 하였을 때 높이는 해당 밑변의 법선 벡터에 $\vec{v}\Delta t$를 내적해줌으로써 얻을 수 있다.
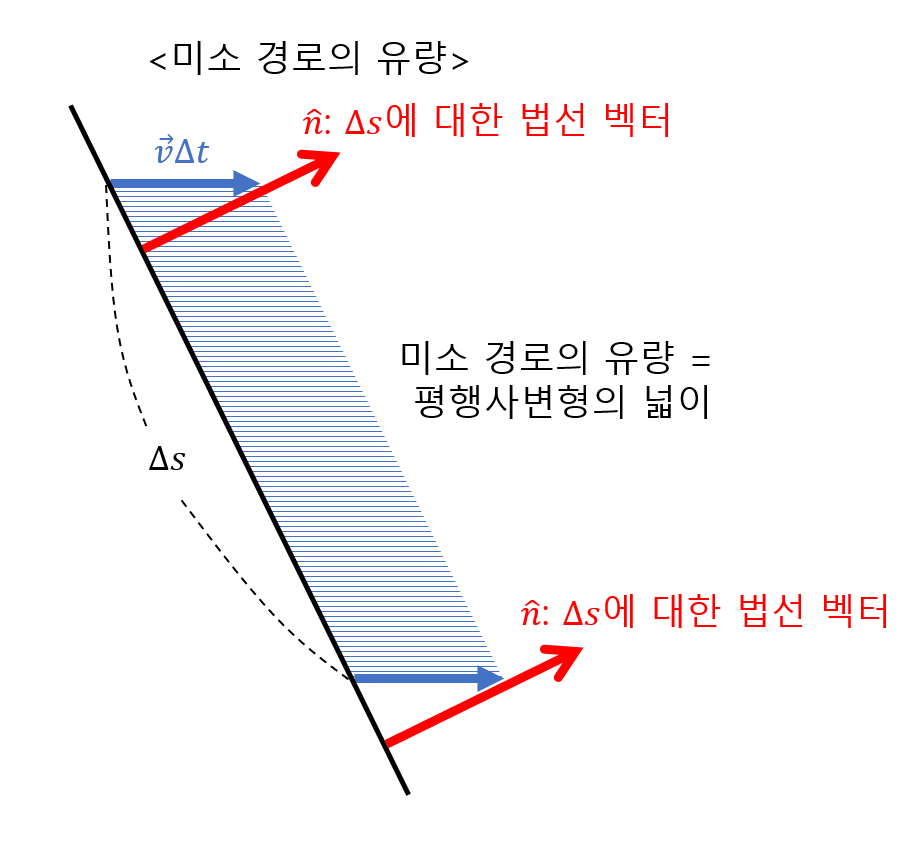
그림 4. 평행사변형의 넓이를 계산하기 위해선 밑변에 높이를 곱해야 하며, 평행 사변형의 높이는 벡터 vΔt에 Δs의 법선 벡터를 내적해줌으로써 얻을 수 있다.
즉, 평행사변형의 넓이, 즉 유량은 다음과 같다.
\[유량 = \Delta s(\vec{v}\Delta t \cdot \hat{n})\]flux의 개념은 단위시간 당 빠져나간 유량을 의미하므로, 위 식을 $\Delta t$로 나눠주면,
\[flux_{\Delta s}= \Delta s(\vec{v} \cdot \hat{n})\]이다.
결국 전체 경로에 대한 flux는 다음과 같다.
\[\sum flux_{\Delta s}=\sum (\vec{v} \cdot \hat{n})\Delta s\]여기서 $\Delta s$를 매우 작게 만들어주고, $\vec{v}$ 대신에 일반적인 벡터장을 나타내는 기호로써 $\vec{F}$를 쓰면 flux의 식을 유도할 수 있게 된다.
\[\text{2D flux} = \int_C\vec{F}\cdot\hat{n}ds\]여기서 일반적으로 법선 벡터($\hat{n}$)의 방향은 경로를 따라가는 방향의 우측 방향이 양의 방향으로 생각한다.
flux의 실제적인 계산을 위한 추가 조치
식 (6)을 보면 flux의 공식이 잘 유도되었다는 것은 알 수 있지만, 실제로 flux를 계산하기 위해선 $\hat{n}$이나 $ds$가 하나의 변수에 대해 정리되어야 한다.
보통 임의의 경로를 표현하기 위해서는 매개변수 방정식을 이용하므로, 자주 사용되는 매개변수인 $t$에 대해 flux의 식을 조금 더 다듬어보자.
법선 벡터 계산
경로의 법선 벡터를 계산해주기 위해선 접선 벡터의 개념으로부터 출발해보자.
어떤 경로 $r$이 매개변수 방정식으로 다음과 같이 주어져 있다고 생각해보자.
\[r(t) = x(t)\hat{i} + y(t)\hat{j}\]접선 벡터라는 것은 해당 경로에 대한 시간 미분을 의미하므로,
\[r'(t) = x'(t)\hat{i} + y'(t)\hat{j}\]이고, 접선 벡터는 크기에 대한 정보는 없이 방향에 대한 정보만 가지므로 접선벡터 $\vec{T}$는
\[\vec{T}(t) = \frac{r'(t)}{|r'(t)|}=\frac{x'(t)\hat{i} + y'(t)\hat{j}}{\sqrt{x'(t)^2 + y'(t)^2}}\]이다.
여기서 회전변환행렬을 이용해서 접선벡터로부터 법선벡터를 계산해보자.
일반적으로 회전 각도 $\theta$(시계반대방향 기준)에 대해 회전 행렬은 다음과 같다.
\[\begin{bmatrix} \cos\theta & -\sin\theta\\ \sin\theta & \cos\theta \end{bmatrix}\]아래 그림과 같이 법선 벡터는 접선 벡터를 $-90’$ 회전 시켜줌으로써 얻을 수 있다.
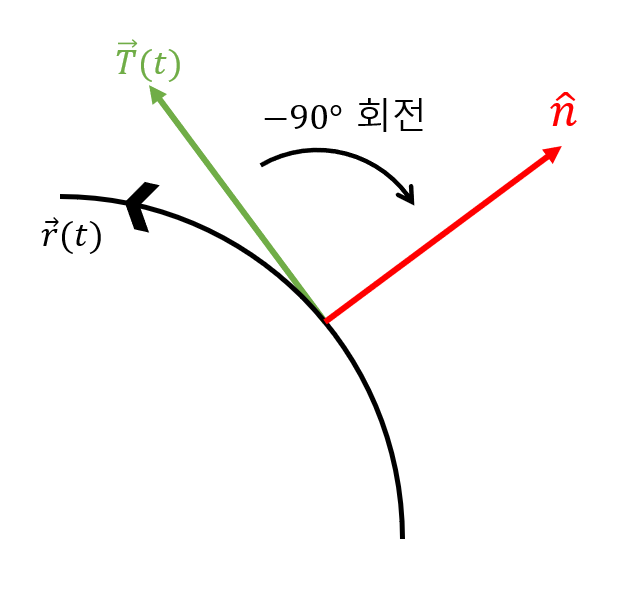
그림 5. 접선벡터와 법선벡터의 관계
$\cos(-90’)$는 0이고, $\sin(-90’)$는 -1이므로 회전변환행렬은
\[\begin{bmatrix} 0 & 1\\ -1 & 0 \end{bmatrix}\]이므로, 임의의 벡터 $[x, y]^T$에 대해 위의 회전행렬을 적용하면,
\[\begin{bmatrix} 0 & 1\\ -1 & 0 \end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}y\\-x\end{bmatrix}\]임을 알 수 있다. 즉, 어떤 벡터를 $-90’$ 회전시켜주려면 벡터의 두 컴포넌트를 바꿔주고 바뀐 $y$ 컴포넌트에는 -1을 곱해주면 되는 것이다.
따라서, 접선벡터를 이용해 법선 벡터를 계산해주면,
\[식(9) \Rightarrow \frac{y'(t)\hat{i}-x'(t)\hat{j}}{\sqrt{x'(t)^2 + y'(t)^2}} = \hat{n}(t)\]ds 계산
$ds$는 피타고라스 정리에 의해
\[ds = \sqrt{dx^2+dy^2}\]이며, 매개변수 방정식을 이용하면,
\[ds = \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2 }dt = \sqrt{x'(t)^2 +y'(t)^2}dt\]임을 알 수 있다.
법선벡터와 ds의 식을 종합하면,
법선벡터와 ds를 모두 매개변수 $t$에 대한 식으로 표현해주면 다음과 같다.
\[\int_C\vec{F}\cdot\hat{n}\text{ }ds = \int_C\vec{F}\cdot \frac{y'(t)\hat{i}-x'(t)\hat{j}}{\sqrt{x'(t)^2 + y'(t)^2}} \sqrt{x'(t)^2 +y'(t)^2}dt\] \[=\int_C\vec{F}\cdot\left(\frac{dy}{dt}\hat{i}-\frac{dx}{dt}\hat{j}\right)dt\] \[=\int_C\vec{F}\cdot\left(dy\hat{i}-dx\hat{j}\right)\]여기서 우리가 보통 벡터장 $\vec{F}(x,y)$를 다음과 같이 적어왔던 것을 생각해보면,
\[F(x,y) = P(x,y)\hat{i} + Q(x,y)\hat{j}\]$t$가 $a$에서 $b$까지 변한다고 한다면,
\[식(18) = \int_{t=a}^{t=b}Pdy-Qdx\]이다.
예시 문제 풀이
다음과 같이 벡터장 $\vec{F}$가 주어져있을 때, $(3,0)$에서 $(0, 3)$으로 향하는 직선에서의 flux 값을 계산하시오.
\[\vec{F}=2\hat{i}\]
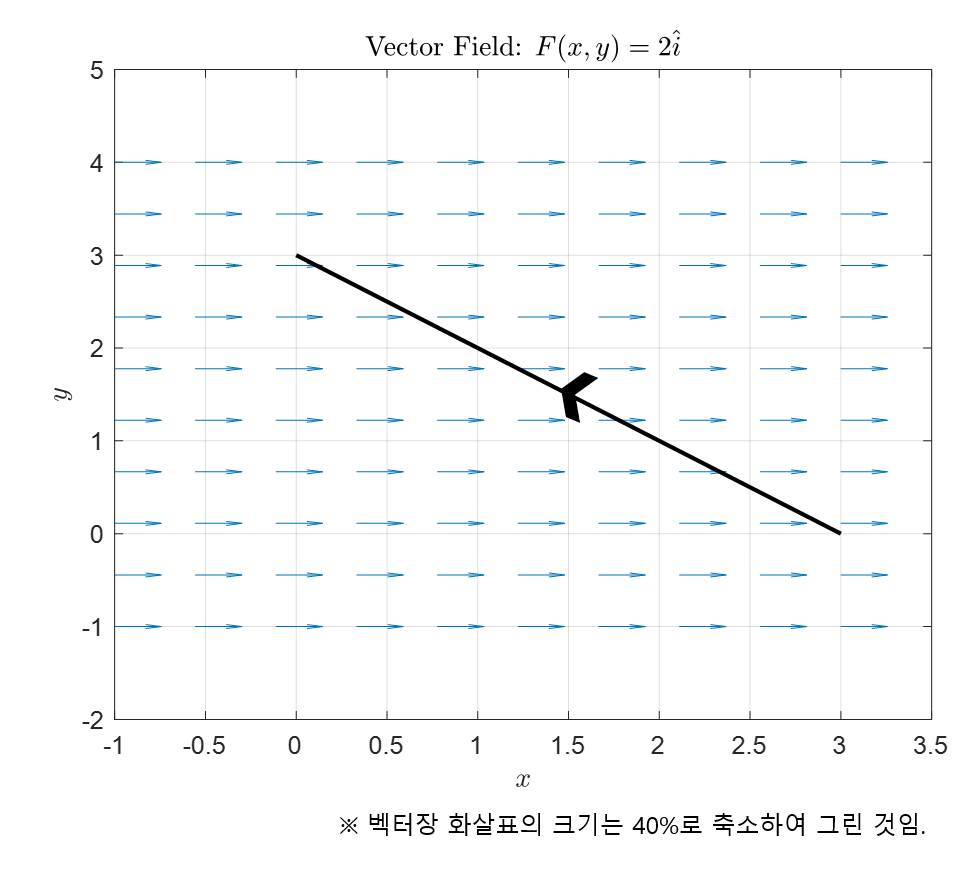
그림 6. 예시 문제에서 주어진 벡터장과 경로
우선, 매개변수를 이용해서 $x(t), y(t)$를 표현해보자.
\[\begin{bmatrix} x(t) = 3-3t\\ y(t) = 3t \end{bmatrix}\text{ where }0\le t \le 1\]이며,
\[\begin{bmatrix} dx = -3dt\\ dy = 3 dt \end{bmatrix}\text{ where }0\le t \le 1\]이다.
flux 값을 계산해보면,
\[\int_C\vec{F}\cdot \hat{n}=\int_{t=0}^{1}Pdy-Qdx\] \[=\int_{t=0}^{1}2\cdot (3dt)-(0)(-3dt)\] \[=6\int_{t=0}^{1}dt=6\]이다.