선형회귀

Gradient descent로 풀어내는 Linear Regression.
Linear Regression이 말하는 것: 수많은 점들을 최대한 잘 설명할 수 있는 trend line을 그으려면 어떻게 해야할까?

선형대수학의 관점에서 본 회귀분석

※ 최적화 문제 관련 내용으로 궁금한 사람은 $\lt$선형대수학의 관점에서 본 회귀분석 $\gt$ 파트를 건너뛰어도 무관함.

prerequisites

이 내용에 대해 이해하기 위해선 아래의 내용에 대해 알고 오는 것이 좋습니다.

선형연립방정식을 이용한 solution 찾기

중학교 시절 연립방정식에 대해 배운 적 있을 것이다.

연립방정식은 2개 이상의 미지수를 포함하는 방정식의 조를 말하는데, 보통 중, 고등학교 과정에서는 이원 일차 연립방정식을 푸는 경우가 많았던 것 같다.

보통의 연립 방정식의 꼴은 아래와 같이 쓸 수 있겠다.

\[\begin{cases} ax + by = p \\ cx + dy = q \end{cases}\]

우리는 이번에 미지수의 개수보다 데이터가 훨씬 많은 경우에 대해 적절한 solution을 찾는 과정을 통해 linear regression에 대해 생각해보고자 한다.

가령, 다음과 같이 세 개의 데이터 포인트가 주어져 있다고 하자.

\[(-1, 0),\text{ }(0, 1),\text{ }(0, 3)\]

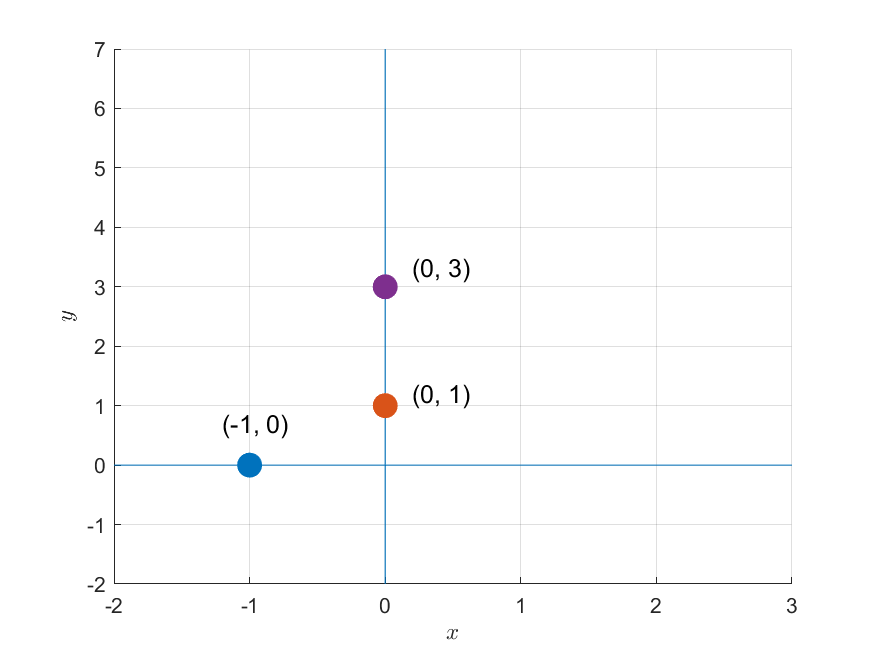
그림 1. 주어진 세 개의 데이터 포인트

만약 이 세 점에 대해 $f(x) = mx+b$와 같은 모델을 통해 이 세 개의 데이터 포인트를 얻었다고 가정하면 아래와 같이 세 개의 방정식으로 구성된 연립방정식을 세울 수 있다.

\[f(-1) = -m + b = 0\] \[f(0) = 0 + b = 1\] \[f(0) = 0 + b = 3\]

이것을 행렬과 벡터를 이용해 표시하면 다음과 같다.

\[(Ax = b) \Rightarrow\begin{bmatrix}-1 && 1 \\ 0 && 1 \\ 0 && 1\end{bmatrix}\begin{bmatrix}m \\ b\end{bmatrix} = \begin{bmatrix}0\\1 \\ 3 \end{bmatrix}\]

이 행렬을 푸는 문제를 기하학적인 관점에서 생각해보면 그림 1과 같이 세 개의 데이터 포인트가 주어졌을 때 이 데이터 포인트들을 모두 통과하는 직선을 구하는 문제와 같다.

2차원 평면 상에 어떻게 선을 놓더라도 이 세 점을 동시에 통과하는 직선을 구할 수는 없다.

다시 말해, 이 문제는 풀릴 수 없다. 해가 존재하지 않기 때문이다.

선형대수학적으로 연립방정식을 보는 관점

선형대수학의 관점에서 연립방정식을 푼다는 것은 아래와 같은 행렬을 푸는 것과도 같이 생각할 수 있는데,

\[A\vec{x} = \vec{b}\]

여기서 벡터와 행렬을 모두 열벡터로 표현하고, $\vec{x}$의 두 요소를 나눠 쓰면 아래와 같다.

\[\Rightarrow \begin{bmatrix} | & | \\ \vec{a}_1 & \vec{a}_2 \\ | & | \end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix} = \begin{bmatrix}\text{ } | \text{ } \\ \text{ } \vec{b} \text{ }\\\text{ } | \text{ }\end{bmatrix}\]

그러면, 위 식은 아래와 같이 생각할 수 있다.

\[\Rightarrow x_1\begin{bmatrix} | \\ \vec{a}_1 \\ | \end{bmatrix} + x_2\begin{bmatrix} | \\ \vec{a}_2 \\ | \end{bmatrix} = \begin{bmatrix}\text{ } | \text{ } \\ \text{ } \vec{b} \text{ }\\\text{ } | \text{ }\end{bmatrix}\]

즉, 열벡터 $\vec{a}_1$와 $\vec{a}_2$를 어떻게 조합하면 $\vec{b}$를 얻어낼 것인가?라는 물음에 적절한 조합 비율인 $x_1$과 $x_2$를 답변해주는 것과 같은 이야기인 것이다.

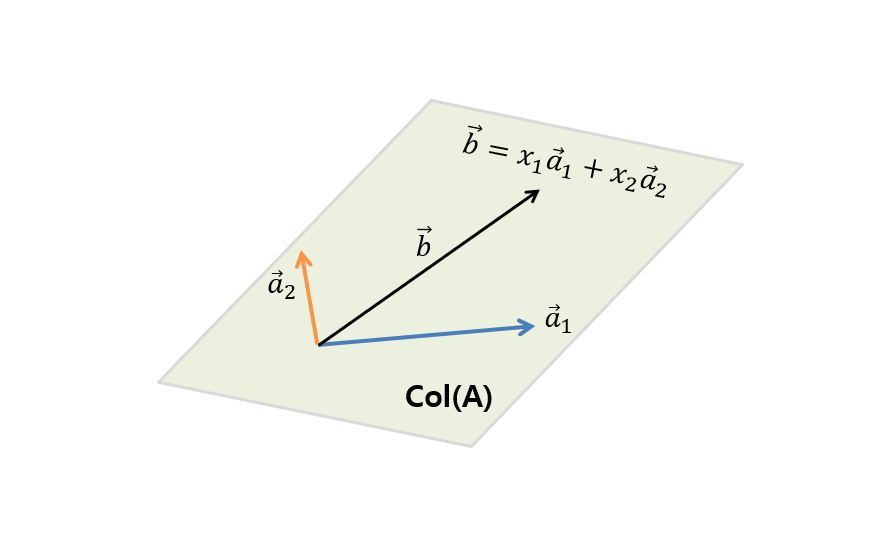
그림 2. A의 열(column)을 이루는 열벡터($\vec{a}_1$, $\vec{a}_2$)의 생성공간(span)인 A의 열공간 $col(A)$에 포함되어 있는 $\vec{b}$를 구하려면 $\vec{a}_1$와 $\vec{a}_2$를 얼마만큼 조합해주어야 할까?

하지만 $\vec{a}_1$과 $\vec{a}_2$를 조합해서 $\vec{b}$를 얻을 수 있으려면 $\vec{b}$는 $\vec{a}_1$과 $\vec{a}_2$를 조합해 얻을 수 있는 모든 경우의 수 중 하나여야 한다.

다시 말해 $\vec{a}_1$과 $\vec{a}_2$의 생성공간(span) 안에 $\vec{b}$가 포함되어 있어야 한다. 이것이 해를 찾을 수 있는 조건이다.

최적의 해를 찾기

꿩대신 닭이라고 했던가. 그림 1과 같은 문제에서 처럼 정확한 정답을 찾을 수 없다면 최대한 정답에 가까운 것이라도 찾아야 한다.

다시 말해 그래도 그나마 가장 세 점의 트렌드를 잘 표현해줄 수 있는 직선을 찾을 수는 있을 것이다.

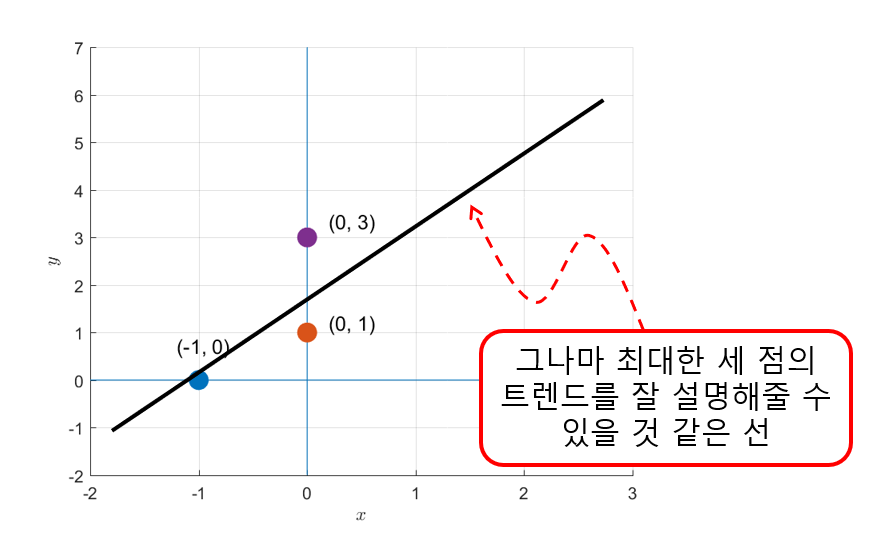
그림 3. 그나마 세 점의 트렌드를 잘 설명해 줄 수 있을 것 같은 직선을 그어보자

여기서, 우리가 점 세 개의 트렌드를 잘 표현해주는 직선을 과정은 선형대수학적으로는 해($\vec{b}$)가 행렬 $A$의 열공간(column space)안에 존재하지 않는 경우 열 공간안에 있는 정답에 가장 가까운 해를 찾는 과정과 일치시켜 생각할 수 있다.

실제로 그림 1 혹은 그림 3의 문제에서 $\vec{a}_1$, $\vec{a}_2$와 이 두 벡터로부터 생성되는 열공간, 그리고 $\vec{b}$를 직접 그려보면 다음과 같다.

그림 4. $[-1, 0, 0]^T$ (파란색)와 $[1, 1, 1]^T$ (주황색) 두 벡터의 생성공간(span)으로 표현되는 열공간과 이 column space에 포함되지 않는 벡터 $[0, 1, 3]^T$ (보라색)

그림 4에 있는 내용을 조금 더 추상적으로 그리면 아래의 그림 5와 같다.

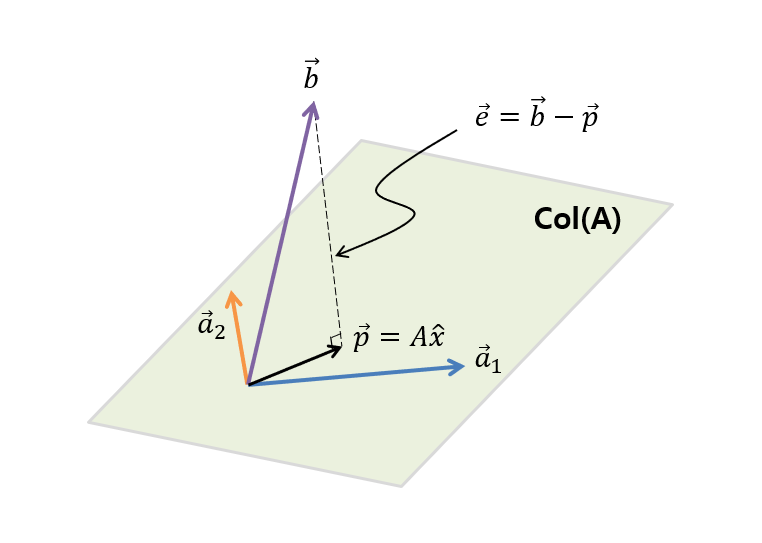
그림 5. A의 열(column)을 이루는 열벡터($\vec{a}_1$, $\vec{a}_2$)의 span인 A의 열공간 $col(A)$와 열공간에 포함되지 않는 $\vec{b}$

그림 5에서 볼 수 있듯이 $\vec{b}$는 $\vec{a}_1$과 $\vec{a}_2$의 열공간 안에 포함되어 있지 않다. 그리고 그림 5에서 확인할 수 있듯이 여기서 우리가 찾을 수 있는 $\vec{b}$와 가장 가까우면서 $\vec{a}_1$과 $\vec{a}_2$의 선형결합을 통해 얻을 수 있는 최적의 벡터는 $\vec{b}$가 열공간(col(A))에 정사영된 $\vec{p}$이며 우리는 이 $\vec{p}$를 계산해줌으로써 벡터 $\vec{a}_1$과 $\vec{a}_2$를 얼마만큼 선형조합 해주어야 할지($\hat{x}$)를 알 수 있게 된다.

그렇다면 원래의 해 $\vec{b}$와 정사영 벡터 $\vec{p}$의 차이 벡터를 $\vec{e}$라고 하면 $\vec{e}$는 행렬 $A$의 어떤 벡터와도 직교하므로 다음이 성립한다.

\[A\cdot\vec{e} = \begin{bmatrix} | & | \\ \vec{a}_1 & \vec{a}_2 \\ | & | \end{bmatrix}\cdot\vec{e} = 0\]

여기서 ‘$\cdot$’은 내적 연산이다.

즉, 내적을 계산해주면,

\[A^Te = A^T(\vec{b}-A\hat{x}) = 0\] \[\Rightarrow A^T\vec{b}-A^TA\hat{x} = 0\] \[\Rightarrow A^TA\hat{x} = A^T\vec{b}\] \[\therefore \hat{x}=(A^TA)^{-1}A^T\vec{b}\]

이라는 것을 알 수 있다.

기본 부분공간들을 이용한 설명

그림 5의 $\vec{e}$는 column space 상에 있는 모든 벡터들과 직교한다.

이것을 4개 주요 부분 공간의 관계편에서 본 내용을 토대로 생각하면 $\vec{e}$는 left nullspace에 있는 벡터임을 알 수 있다.

다시 말해 벡터 $\vec{b}$는 column space 상에서 만들 수 있는 기저벡터들과 left null space 상에서 만들 수 있는 기저벡터들을 합친 기저벡터들로만 구성할 수 있는 공간에 위치하고 있으며 $\vec{p}$는 그 중 가장 가까운 column space 상에 있는 벡터, $\vec{e}$는 left null space 상에 있는 벡터를 의미하게 된다.

그림으로 표시하면 아래와 같다.

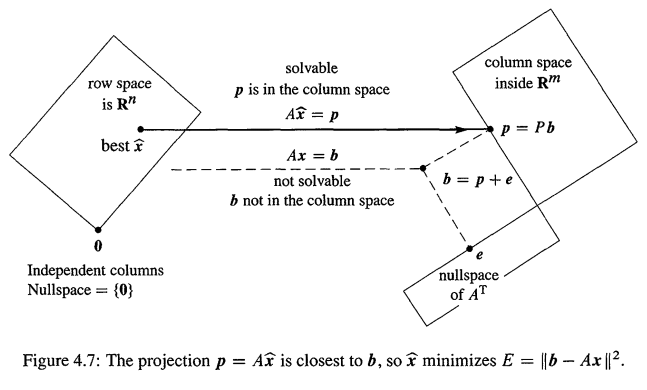
그림 6. 선형대수학적으로 생각하는 선형회귀에 대한 기본 공간들간의 관계
그림 출처: Introduction to Linear Algebra, Gilbert Strang

여기서 null space가 ${0}$인 것은 만약 null space가 영공간이 아니라면 함수의 형태는 완전 세로 방향으로 가는 모양일 것이기 때문인데, 이 때는 함수가 정의될 수 없기 때문에(즉, 기울기가 무한히 커지는 상태) 선형회귀 모델을 이용해 풀어서 어떤 함수를 얻고자 한다면 null space가 영공간이 아닌 경우는 제외하는 것이기 때문이다.

실제 계산

MATLAB으로 아래와 같이 $A$, $b$를 설정하고 $\hat{x}$를 구할 수 있다.

A = [-1, 1; 0, 1; 0, 1];
b = [0; 1; 3];

x_hat = inv(A'*A)*A'*b;

계산 결과는

x_hat =

     2
     2

이다.

즉, 아래의 그림 7에서 표현된 것과 같은 기울기가 2이고 절편이 2인 직선이 그림 1, 3에서 본 세 점의 트렌드를 제일 잘 설명해줄 수 있는 점이라는 의미이다.

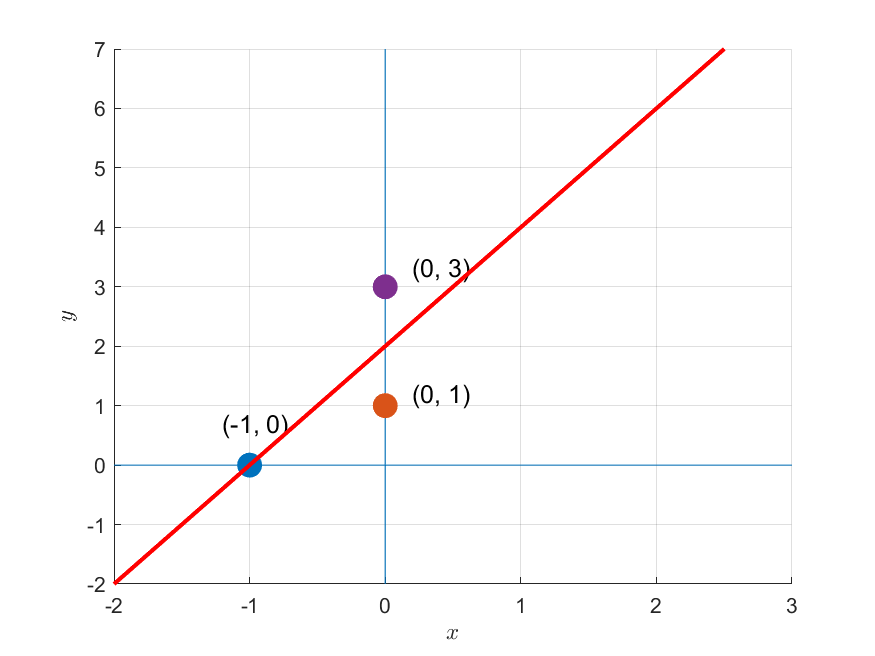
그림 7. 그림 1과 그림 3에서 본 데이터에 대한 최적의 회귀식

최적화 문제 관점에서 본 회귀분석

※ 선형대수학 관련 내용으로 궁금한 사람은 $\lt$최적화 문제 관점에서 본 회귀분석$\gt$ 파트를 건너뛰어도 무관함.

prerequisites

최적화 관점에서 본 회귀분석을 이해하기 위해서는 아래의 내용에 대해 알고 오시는 것이 좋습니다.

최적화 문제 관점에서 본 회귀분석 소개

최적화 관점에서 보는 회귀분석은 데이터에 대한 모델 설정으로부터 시작할 수 있다.

가령 아래 그림과 같이 두 개의 특성을 갖는 데이터가 있다고 생각해보자.

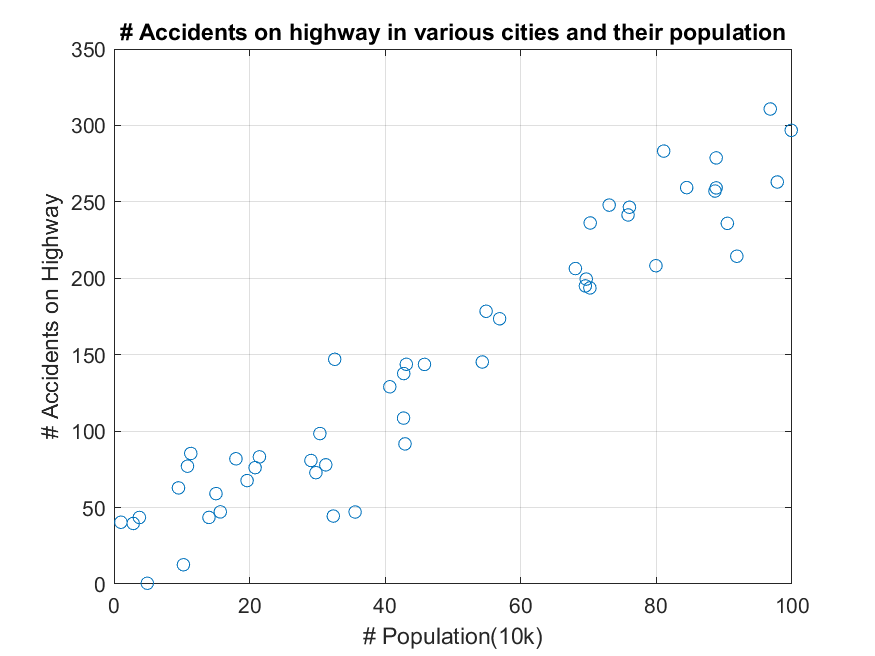
그림 8. 서로 상관관계를 가지고 있는 특성(feature)쌍

이 데이터는 특정 주(states)의 인구수와 각 주에서 일어난 교통사고 건수를 각각 x, y 축에 표시한 것이다.

우리는 이 데이터에 대한 모델을 가정해보고자 한다.

데이터의 형태를 볼 때 직선 모델을 이용한다면 어떻게든 이 데이터를 모델링하는데는 무리가 없어 보인다.

즉, 우리의 모델은 아래와 같이 두 개의 파라미터를 가지는 1차 함수라고 할 수 있다.

\[y = f(x) = ax+b\]

하지만 이 모델의 파라미터 $a$, $b$는 어떻게 정해야 할까? 다시 말해 어떤 직선이 우리의 데이터를 가장 잘 설명해주는 걸까?

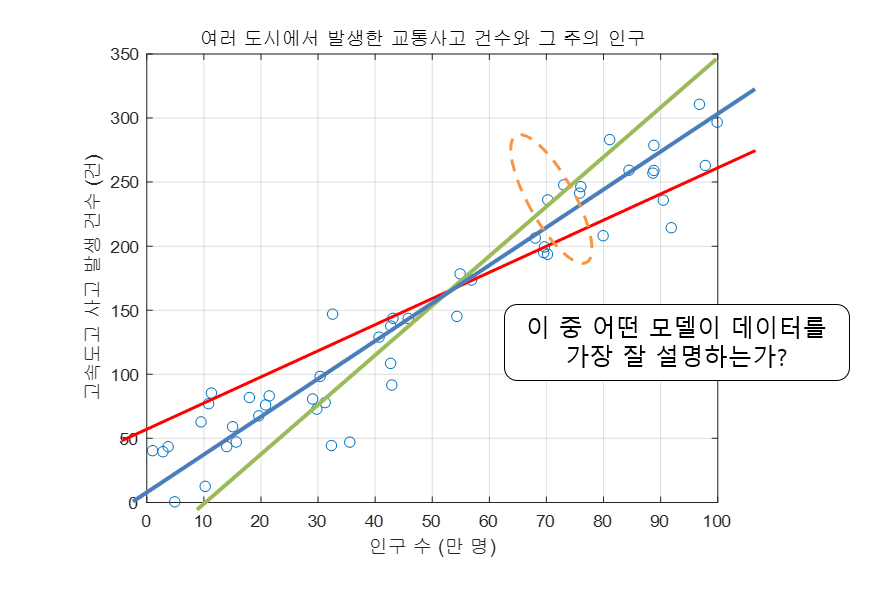
그림 9. 어떤 모델이 이 데이터의 특성(feature)쌍의 관계를 제일 잘 설명해주는 걸까?

비용 함수 정의하기

우리는 여기서 어떤 직선이 우리의 데이터를 가장 잘 설명해주는 모델인지 결정할 수 있어야 한다.

여기서 ‘가장 잘 설명한다’는 말을 다른 말로 정의하자면 모델과 데이터 간의 격차가 가장 적어야 한다고 말할 수도 있을 것 같다.

다시 말해 전체 데이터에 대해 평균적으로 오차(error)가 가장 작은 모델이 더 좋은 모델이라고 말할 수 있다. 우리는 어떤 $i$ 번째 데이터 포인트에 대한 오차($e$)를 다음과 같이 정의해볼 수 있을 것이다.

우리의 직선 모델로부터 계산된 $y$축의 feature 값을 $\hat{y}_i$라고 하고, 데이터에서 주어진 $y$축의 feature 값을 $y_i$라고 하면,

\[e_i = \hat{y_i} - y_i\]

라고 생각할 수 있다.

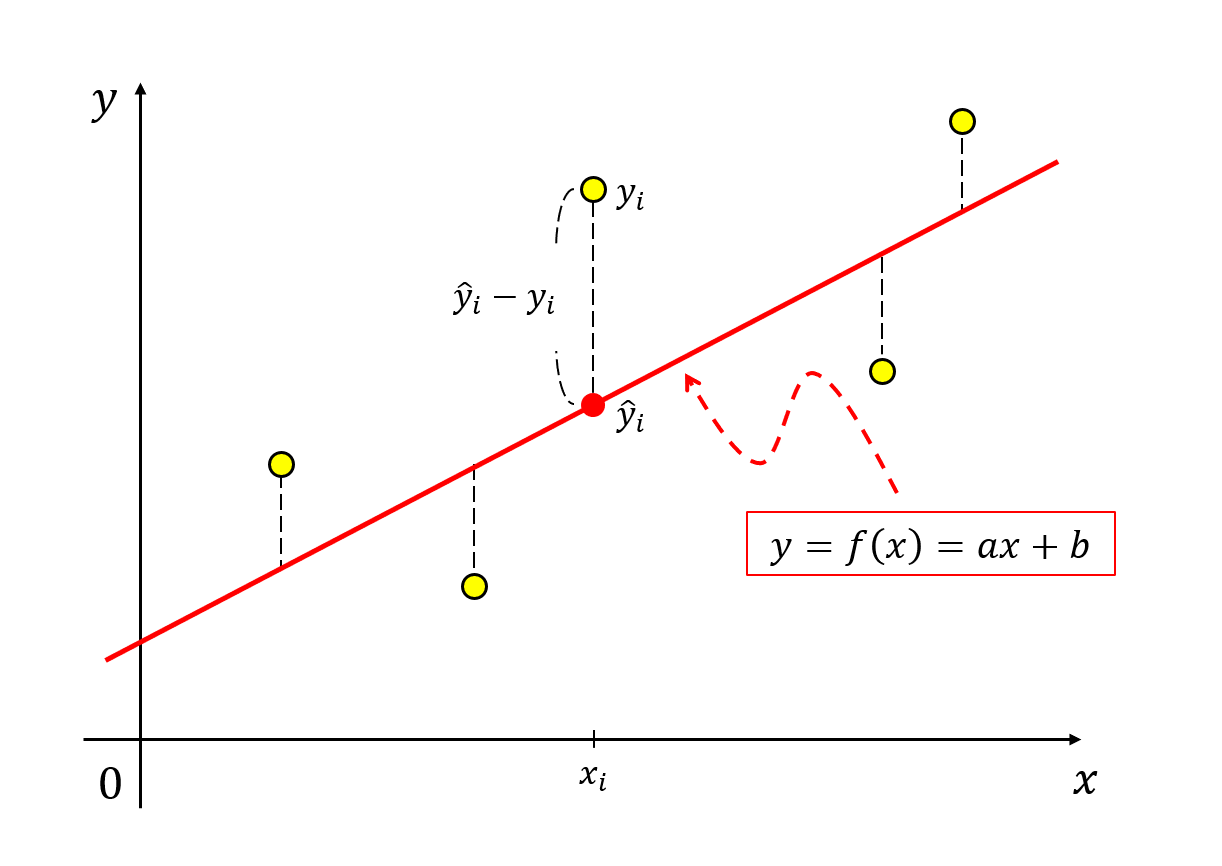
그림 10. 선형 모델의 예측값과 실제 데이터 간의 차이

여기서 오차의 부호에 대한 고민 자체를 애초에 하지 않으려면 오차를 다음과 같이 정의하는 것도 좋을 것이다.

\[e_i = (\hat{y_i} - y_i)^2\]

후에 더 설명하겠지만, 오차는 미분해서 쓸 것이기 때문에 미분 과정의 수식을 조금 더 깔끔하게 해주기 위해 다음과 같이 정의하는 것도 좋은 아이디어다.

\[e_i = \frac{1}{2}(\hat{y_i} - y_i)^2\]

이제 데이터의 총 수가 $N$이라고 하면, 모든 데이터에 대한 평균적인 오차는 다음과 같이 계산할 수 있다.

\[E = \frac{1}{N}\sum_{i=1}^Ne_i = \frac{1}{N}\sum_{i=1}^N\frac{1}{2}(\hat{y_i} - y_i)^2 = \frac{1}{2N}\sum_{i=1}^{N}(\hat{y_i} - y_i)^2\] \[=\frac{1}{2N}\sum_{i=1}^{N}\left(ax_i+b-y_i\right)^2\]

여기서 우리의 모델은 $f(x) = ax+b$이므로 $\hat{y}_i = ax_i + b$로 계산하였다.

비용 함수의 시각화

앞서 계산한 $E$는 소위 말하는 ‘비용 함수(cost function)’라고 부르기도 하는데, 이 비용함수 값이 작을 수록 데이터에 대한 설명 능력이 좋다고 볼 수 있다.

우리의 데이터 $x_i$와 $y_i$는 주어진 것이기 때문에 비용함수 $E$를 $a$와 $b$에 대한 함수로 봐도 좋을 것이다.

즉,

\[E=f(a, b) = \frac{1}{2N}\sum_{i=1}^{N}\left(ax_i+b-y_i\right)^2\]

이라고 쓸 수 있다.

그렇다면, 우리가 데이터를 잘 설명하는 회귀모델을 찾는다는 것은 $E$를 최소화해주는 $a$와 $b$를 찾는 문제로 바꿔 생각할 수 있다. 즉, $E$의 최소값을 찾는 문제로 환원해 생각할 수 있는 것이다.

이것을 시각화해보자면 아래의 그림 11에서와 같이 slope(즉, 위에서 $a$에 해당)와 intercept(즉, 위에서 $b$에 해당)가 정의역인 공간에서 cost function $E$가 스칼라 함수로 존재한다고 할 수 있다.

그림 11. slope와 intercept가 정의역인 공간에서 cost function과 그 최솟값(별표)
※ 비용 함수의 parameter들은 모두 normalize하여 시각화하였음.

즉, 그림 11에서 볼 수 있는 최소값을 찾기 위해선 어떻게 하는 것이 좋을까?

Gradient Descent를 이용한 최소 비용함수 계산

함수의 최솟값을 찾는 방법은 정말 다양하지만, 일반적으로 회귀모델 비용 함수의 최솟값을 찾는 문제를 해결하기 위해 경사하강법(gradient descent)이 가장 많이 이용된다.

짧게나마 경사하강법을 복습해보자면, 높은 곳에서 낮은 곳으로 비탈길을 타고 내려갈 때에는 한발 한발 씩 가장 경사진 방향으로 내려가는 방법을 수학적으로 써놓은 알고리즘이라고 할 수 있다.

gradient의 의미를 생각하면 gradient에 대해 생각해볼 것은 gradient는 기울기가 ‘커지는’ 방향으로 정의된다는 점이다.

아래의 그림을 보면 검은색 점으로 표현한 곳에서 임의로 gradient descent 알고리즘을 시작한다고 하면 gradient의 방향은 다음과 같이 빨간색 화살표로 생각할 수 있다.

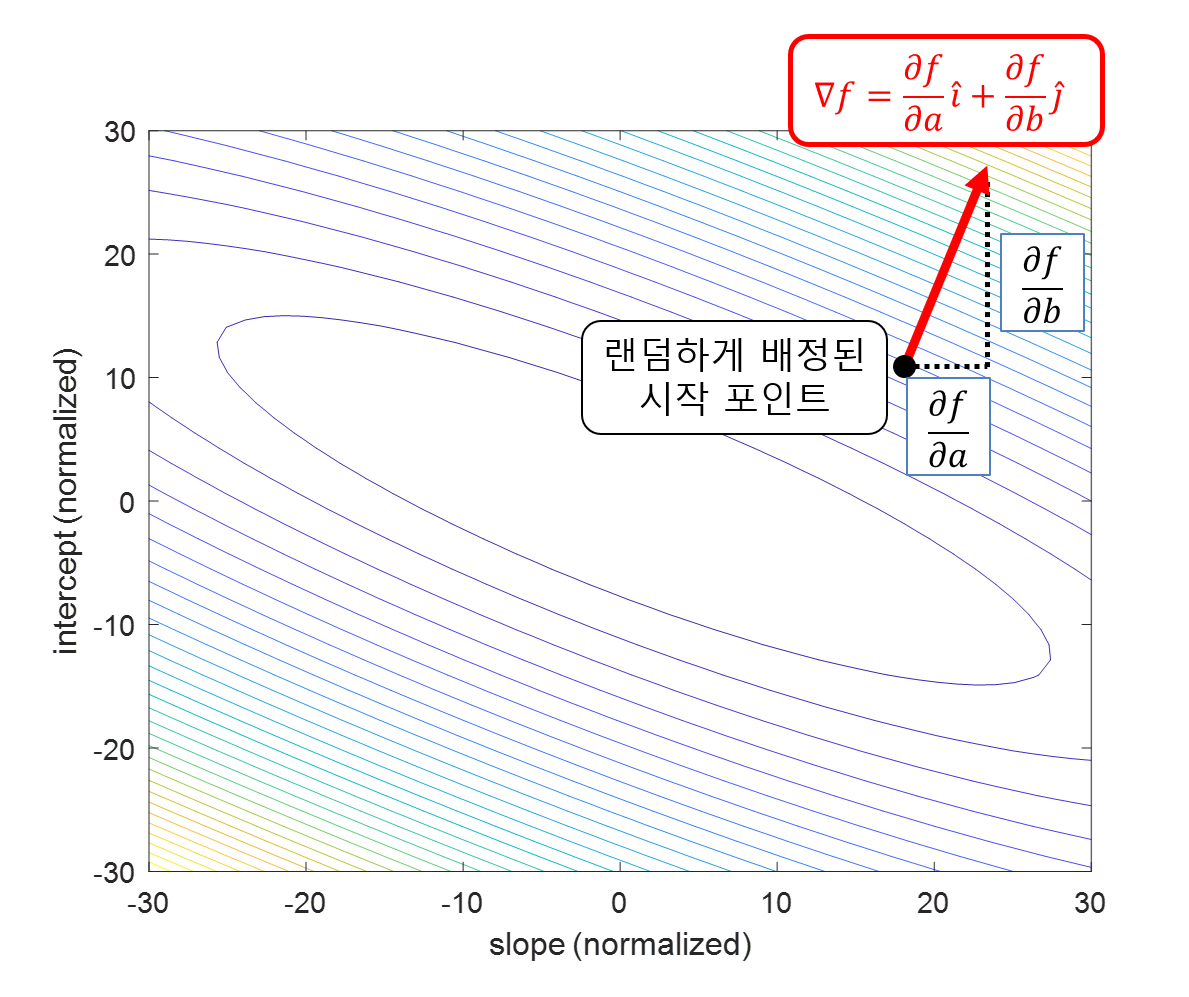
그림 12. 정의역이 $a$ 와 $b$ (여기선 slope, intercept)이고 높이가 비용함수의 값인 함수 공간에서 임의의 포인트에서의 gradient 방향은 함수값이 커지는 방향이다.

따라서 gradient의 방향은 함수가 ‘커지는’ 방향이므로 우리는 이 반대 방향으로 한 스텝, 한 스텝 $a$와 $b$의 위치를 업데이트 해간다면 결국은 비용함수 $E=f(a,b)$의 최소값(별표) 위치까지 $a$, $b$를 옮겨갈 수 있을 것이다.

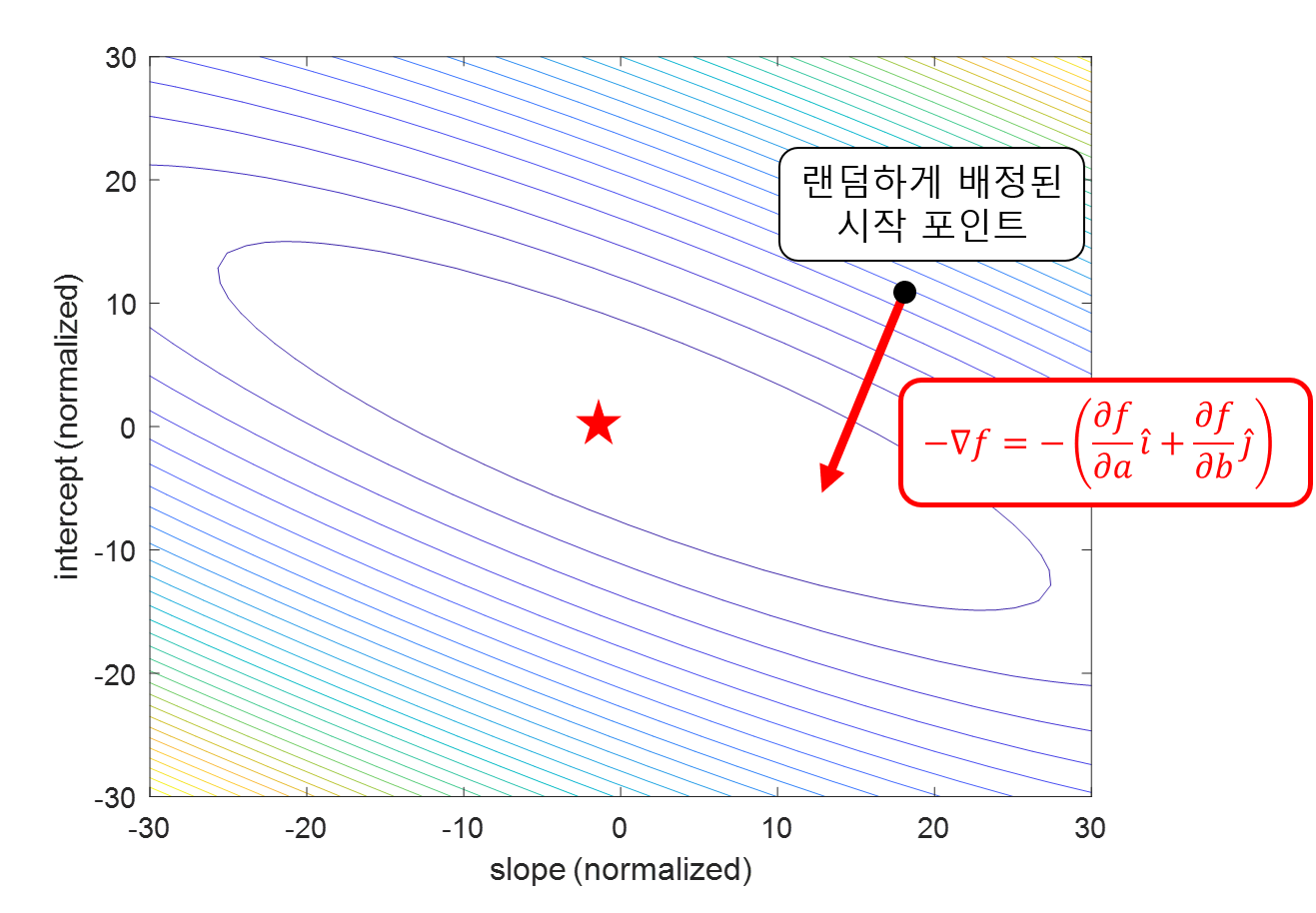
그림 13. 정의역이 $a$ 와 $b$ (여기선 slope, intercept)이고 높이가 비용함수의 값인 함수 공간에서 임의의 포인트에서 gradient의 반대방향으로 $a$와 $b$의 위치를 업데이트 해간다면 결국 비용함수가 최소가 되는 $a$와 $b$를 찾아갈 수 있을 것이다.