Prerequisites
이 포스트를 잘 이해하기 위해선 아래의 내용에 대해 알고 오시는 것이 좋습니다.
여러 표본 집단을 비교하는 방법
연구나 조사를 수행하다보면 여러 표본집단들의 평균을 비교할 필요가 있다.
예를 들어, 두 가지 음식 A, B가 몸무게에 어떤 영향을 주는지 확인하는 조사를 진행한다고 하자.
이 질문에 답하기 위해선 다음과 같이 연구를 진행할 수 있다.
우선 피험자간 몸무게에 큰 차이가 없는 피험자 집단을 모집하고, 해당 집단을 세 그룹으로 나눈 다음 대조군 한 그룹과 음식 A, B만을 먹는 그룹으로 총 세 그룹을 선정해 각각 식이 조절을 시킨다.
그런 뒤에 세 그룹 간의 몸무게 차이가 있는지 “그룹 차이에 관한 적절한 지표”를 만들어 확인하면 되는 것이다.
세 그룹이 각각 음식을 먹고 적당한 시간이 지난 뒤에 측정한 몸무게의 분포가 그림1과 같았다고 생각해보자.
피험자간 몸무게에 큰 차이가 없다고 가정하였으므로, 여러 표본집단들은 하나의 모집단에서 추출된 표본들이라고 볼 수 있다.
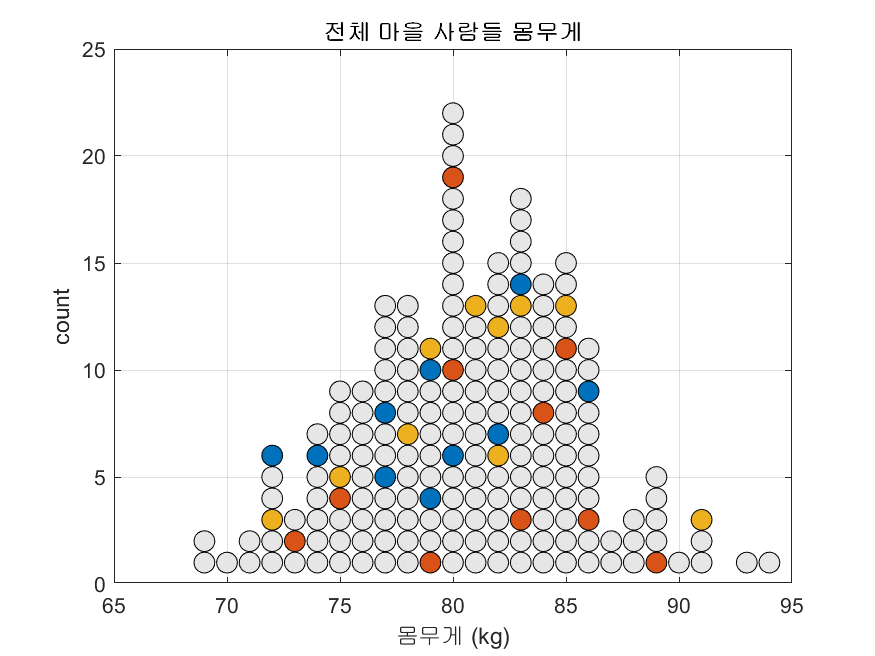
그림 1. 모집단에서 추출된 세 그룹을 도시한 것. 각각의 동그라미들은 사람 한명씩을 의미하고, 서로 다른 색깔은 서로 다른 표본집단을 의미함.
그림 1을 보게 되면 음식 A, B가 몸무게에 특별한 영향을 주지 않는 다는것을 알 수 있다.
그렇지만, 실제 연구 과정에서는 우리는 전체 모집단에 대해서 확인하는 것은 어렵고 표본 집단들의 분포들만 확인할 수 있다.
각 그룹별 표본집단들만을 따로 도시하면 그림 2와 같다.
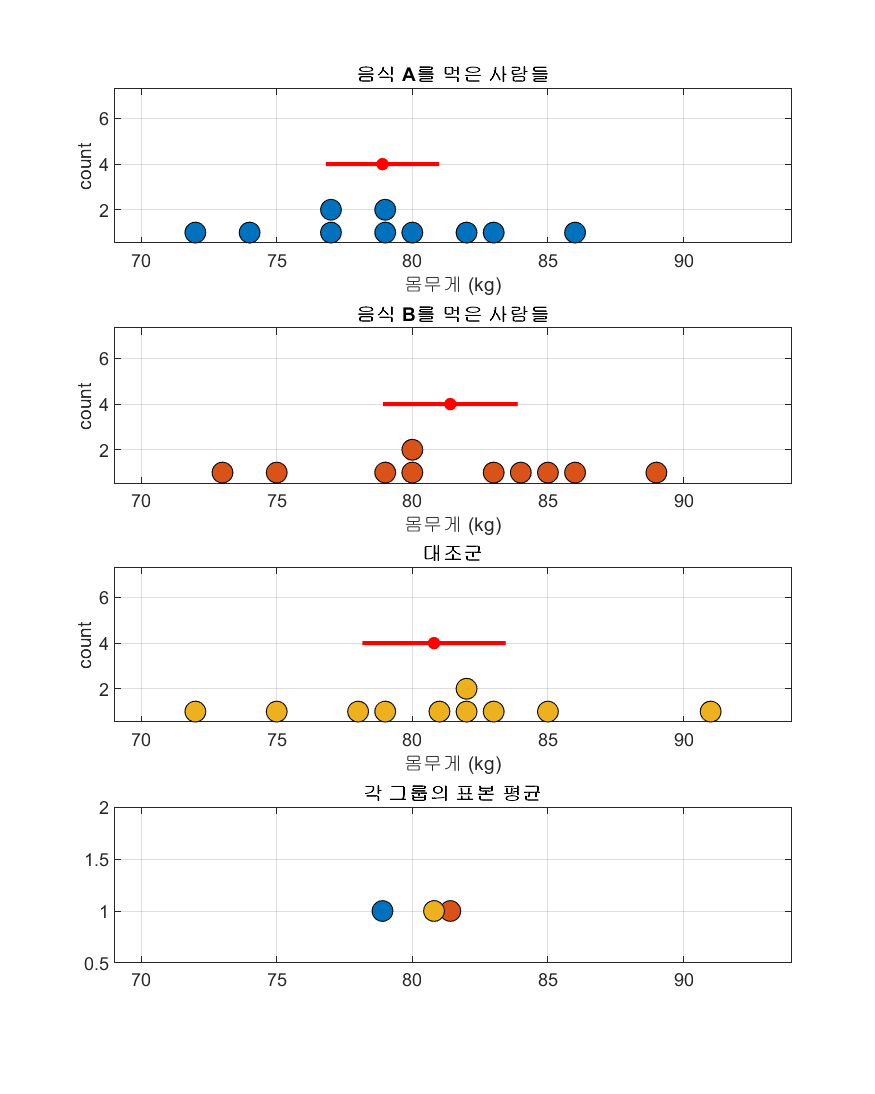
그림 2. 음식 A, B와 대조군에 대해 각 표본집단별로 도시하였을 경우. 빨간 점과 빨간 선은 각 표본 그룹의 평균과 표준편차를 나타내고 있다.
그림 1에서 보았을 때와는 다르게, 그림 2만 보게 되면 표본 집단별로 평균적인 차이가 있는 것 처럼 보이기도 한다. 특히 그림 2의 가장 아래의 subplot을 보게 되면 표본 평균이 약간의 차이를 보이긴 한다는 것 또한 확인할 수 있다.
그림 1과 그림 2에서 확인한 결과들을 종합해보면 그룹 간 차이에 대해 다음과 같이 생각할 수 있다.
이 차이는 음식의 영향일까? 아니면 다른 이유로 몸무게가 (랜덤하게) 변했기 때문일까? ㅡ질문(☆)
F-value의 의미: 차이 / 불확실도
F-value는 여러 표본 집단을 비교하기 위한 지표이며, 결론부터 말하자면 F-value는 앞서 배운 t-value와 거의 같은 의미를 갖는다.
다시 말해, t-value가 가졌던 의미와 마찬가지로 F-value도 차이 / 불확실도로 표본 그룹 간 차이를 숫자 하나로 서술하고 있는 것이다.
여러 표본 간 차이의 통계적 지표: 그룹 간 차이 정도 / 불확실도
여기서 F-value가 t-value와 약간 차이를 보이는 점은 그룹 간 차이 정도와 불확실도를 약간 변형해 사용한다는 점이다. F-value는 이들로 부터 계산한 분산의 비율을 척도로 이용한다1.
F-value의 논리적 유도
그룹 간 분산, 그룹 내 분산 계산
이제부터는 세 그룹 간의 차이를 확인해보자. 앞서 언급되었듯이 이를 위해서 분산을 이용하고자 한다.
질문(☆)으로 다시 돌아오자면, 음식의 영향과 몸무게의 랜덤한 변화는 모두 ‘분산’으로 설명 가능한 개념이다.
음식의 영향이 컸는지 확인하기 위한 분산은 각 표본집단의 그룹 간 평균이 얼마나 떨어져있는지로 확인할 수 있다.
이 개념은 표본과 표준 오차의 의미편에서 본 것 처럼 각 집단들은 모집단에서 추출한 표본으로 생각할 수 있다.
즉, 표본 집단의 그룹 간 평균의 표준 편차란, 표본 평균의 표준편차, 즉, 표준 오차를 의미한다.
수식으로 쓰자면, 표준 오차는 표본 평균의 표준 편차이므로 각 표본의 크기를 $n$이라 했을 때 다음과 같이 쓸 수 있다.
\[\sigma_{\bar{X}}=\frac{\sigma}{\sqrt{n}}\]따라서, 표본 집단 간 그룹 간 분산은 다음과 같이 쓸 수 있다.
\[\sigma^2_{bet} = n \sigma_{\bar{X}}^2\]여기서 우리는 모분산은 모르고 표본분산을 이용해아하므로 아래와 같이 $\sigma$는 모두 $s$로 대체할 수 있다.
\[s^2_{bet} = n s_{\bar{X}}^2\]한편, 음식 외의 이유에 의한 랜덤한 몸무게의 변화는 그룹 내 분산으로 추정할 수 있는데, 세 그룹에서 부터 얻은 분산 값을 산술평균 해 계산할 수 있다2.
\[s^2_{wit} = \frac{1}{3}(s^2_A + s^2_B + s^2_{con})\]두 분산의 비율 계산
우리는 두 개의 분산을 계산했는데, 이 과정은 결국 두 가지 방법으로 모분산을 추정한 것과 같다.
그리고 우리는 앞서 언급한 아래의 문장에서 생각한 논리를 따라 계산한 두 분산을 나눠주고자 한다.
여러 표본 간 차이의 통계적 지표: 그룹 간 차이 정도 / 불확실도
즉, F-value는 아래와 같은 두 분산의 비율로 계산될 수 있다.
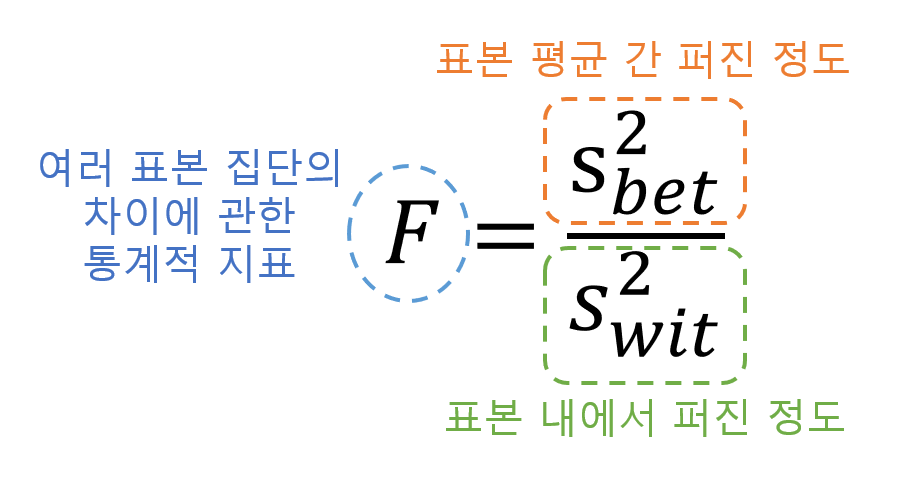
그림 3. F value의 분자 분모가 갖는 의미
그래서 그림 2에서 본 표본 그룹 간의 차이가 랜덤한 이유에 의한 것이라면 두 모분산 추정치의 비율은 1에 가까워야 한다. 같은 모분산을 다른 방법으로 추정한 것이기 때문이다.
한편, 만약 이 값이 1보다 꽤 크다면 sample means 간의 variability가 samples 내의 variability를 이용해 추정한 variability보다 더 크다는 것을 의미한다. 즉, 모든 표본집단들이 하나의 모집단에서 나오지는 않았을 것이라는 것을 시사한다고 할 수 있다.
F-value를 계산하는 예시 문제
※ 문제는 Primer of Biostatistics, Glantz (2011)에서부터 가져왔습니다.
핸드폰 사용으로 인한 남성의 정자 운동 능력 저하에 대한 문제를 풀어보도록 하자.
핸드폰을 평소에 많이 사용하지 않는 그룹과 많이 사용하는 두 그룹에 대해서 F-value를 계산해보고자 한다.
(여기서 각 그룹의 피실험자 수는 모두 61명이다.)
아래의 그림에서 볼 수 있듯이 연구진은 빠르게 움직이는 정자의 비율을 측정하였는데, 핸드폰 사용량이 적은 그룹에서는 평균 49%, 사용량이 많은 그룹에서는 평균 41%로 확인되었으며, 각 그룹의 표준편차는 21%와 22%로 나타났다.
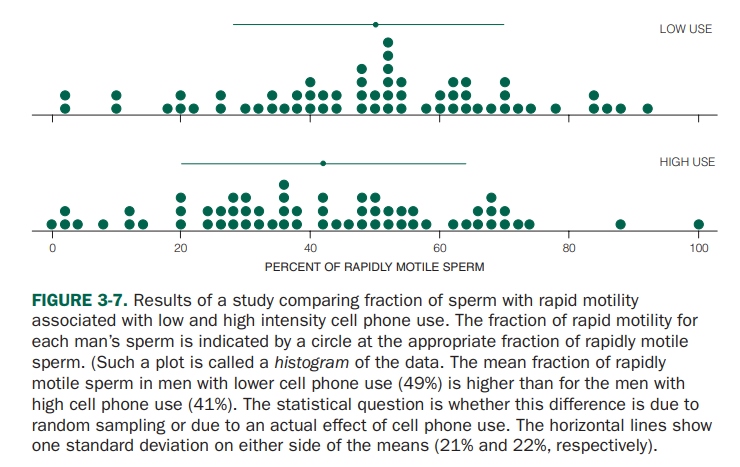
그림 출처: Primer of Biostatistics, Glantz (2011)
두 그룹 간의 차이를 F-value를 이용해서 표현하고자 해보자.
먼저, 그룹 내 분산을 계산해보면 다음과 같을 것이다.
\[s^2_{wit} = \frac{1}{2}\left(s^2_{low}+s^2_{high}\right)\] \[=\frac{1}{2}\left(21^2+22^2\right) = 462.5\%\]그런 다음 그룹 간 분산을 계산해보자. 그룹 간 분산을 계산하기 위해선 표준오차의 값을 계산할 수 있어야 한다.
여기서 표준 오차 각 그룹의 평균이 퍼진 정도, 즉, 각 그룹의 평균이 전체 평균으로부터 얼마나 떨어져있는지를 말하는 것과 같다고 볼 수 있다.
따라서, 전체 데이터의 평균값은
\[\bar{X} = \frac{1}{2}\left(\bar{X}_{low}+\bar{X}_{high}\right)\] \[=\frac{1}{2}(49+41) = 45\%\]이므로, $s_{\bar{X}}$의 값은
\[s_{\bar{X}}=\sqrt{\frac{(\bar{X}_{low}-\bar{X})^2+(\bar{X}_{high}-\bar{X})^2}{m-1}}\] \[=\sqrt{\frac{(49-45)^2+(41-45)^2}{2-1}}=5.66\%\]여기서 각 그룹의 샘플 사이즈는 $n=61$이므로,
\[s^2_{bet}=ns^2_{\bar{X}}=61(5.66^2)=1952\%\]따라서, F-value는 다음과 같이 계산할 수 있다.
\[F=\frac{s^2_{bet}}{s^2_{wit}}=\frac{1952}{462.5}=4.22\]F-분포와 충분히 큰 F의 의미
분산분석(Analysis of Variance, ANOVA)은 위의 과정을 거쳐 계산된 F value가 유의하게 큰지 여부를 확인해서 최소한 한 표본 집단은 다른 모집단에서 나왔는지 여부를 검증한다.
그렇다면 F-value가 충분히 크다는 것은 어떻게 알 수 있는것일까?
t-value의 의미와 스튜던트의 T 테스트편의 “검정 통계량” 꼭지에서 언급했듯이 검정 통계량 중 하나인 F-value는 표본 통계량을 2차 가공한 것과 같다.
표본과 표준오차의 의미편에서 표본 평균의 분포를 계산한 것과 같이 모집단에서 임의의 세 개3 표본 집단을 추출하고 F-value를 계산할 수 있다. 모집단의 수가 150이고 n=10인 표본을 세 개 뽑는 과정을 총 100번 반복하면서 F-value의 분포를 확인해보자.
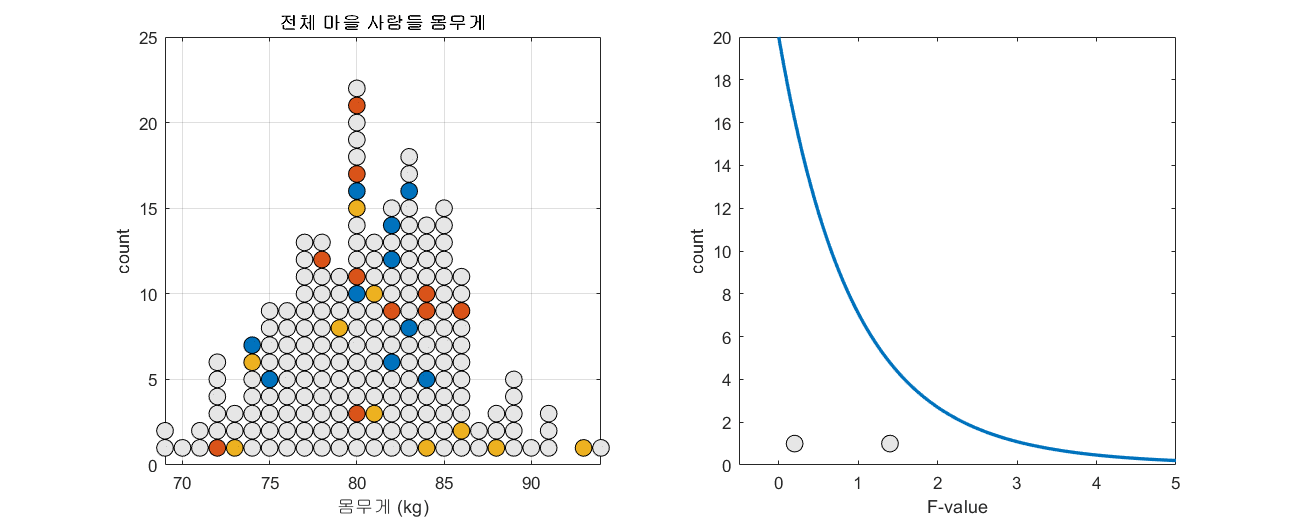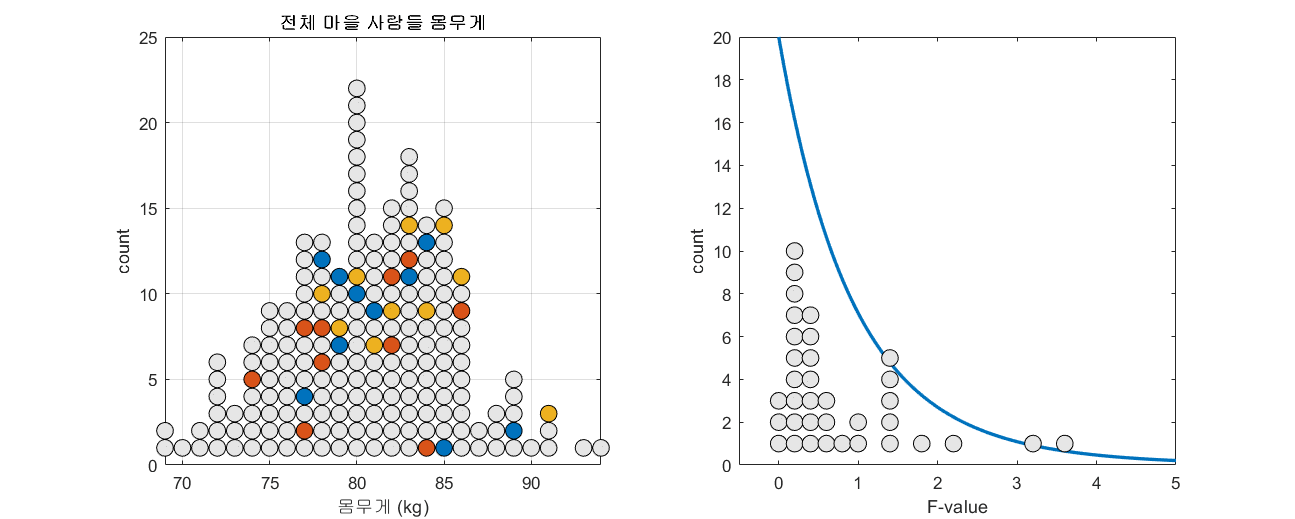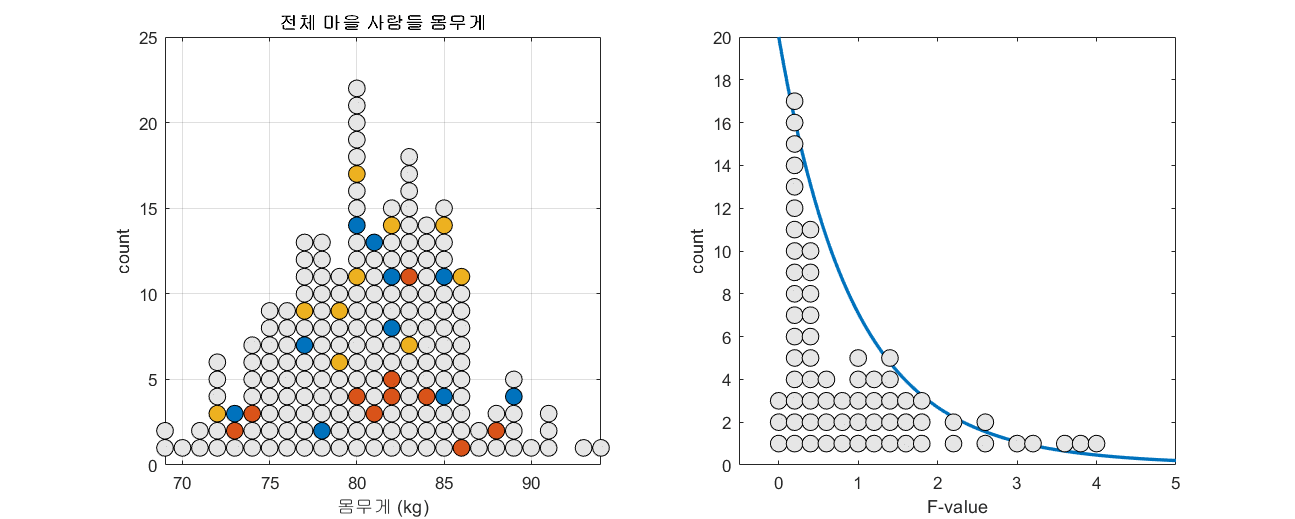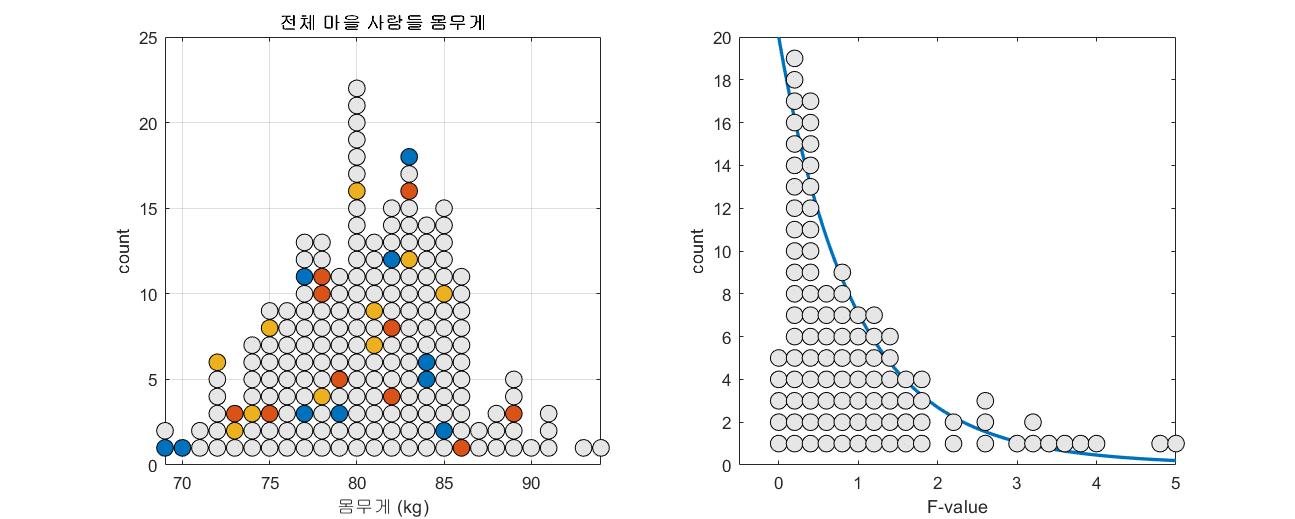
그림 4. 100 번 n=10인 세 개의 표본 그룹을 추출해보고 그 때 마다 얻게되는 F-value를 그린 것
그림 4의 과정을 잘 보면, 하나의 모집단에서 세 개의 표본 그룹을 추출해서 F-value를 구하면 가끔씩 하나의 모집단에서 계산된 F-value임에도 불구하고 3 이상의 높은 값을 가지는 F-value가 계산되기도 한다.
즉, 표본 집단들로부터 충분히 큰 F-value가 계산되었다는 사실이 말해주는 것은 다음과 같다.
표본집단들이 하나의 모집단에서 나왔다고 가정했을 때 이런 큰 F-value가 나왔을 확률은 매우 낮으므로, 이 표본집단들이 하나의 모집단에서 나왔을 것이라는 가정이 맞을 확률 또한 매우 낮다고 말할 수 있다.
사실 그림 4에서와 같은 샘플 추출 과정은 100번이 아니라 거의 무한하다 싶을 정도로 많은 경우의 수가 있을 수 있는데, 모집단의 수가 150이고 n=10인 표본 집단 세 개를 뽑는다고 했을 때 가능한 경우의 수는
\[_{150}C_{30} = 32,198,785,340,494,567,031,466,236,484,400\notag\]가지나 된다.
이처럼 수많은 경우의 수에 대해 표본 추출을 할 수는 없으므로, 수학적으로 F-value들의 분포를 계산하여 공식화 한 것이 F-분포(그림 4 우측에서 실선)라고 할 수 있다.
마지막으로 충분히 큰 F-value는 보통 상위 5% 혹은 1% 등의 값으로 통상적으로 결정하며, 그림 4의 마지막 장면은 그림 5를 참고하여 확인할 수 있으며 시뮬레이션에서 확인한 상위 5%의 F-value는 실제 F-분포 상의 상위 5% F-value(3.35)에서 크게 벗어나지는 않았다.
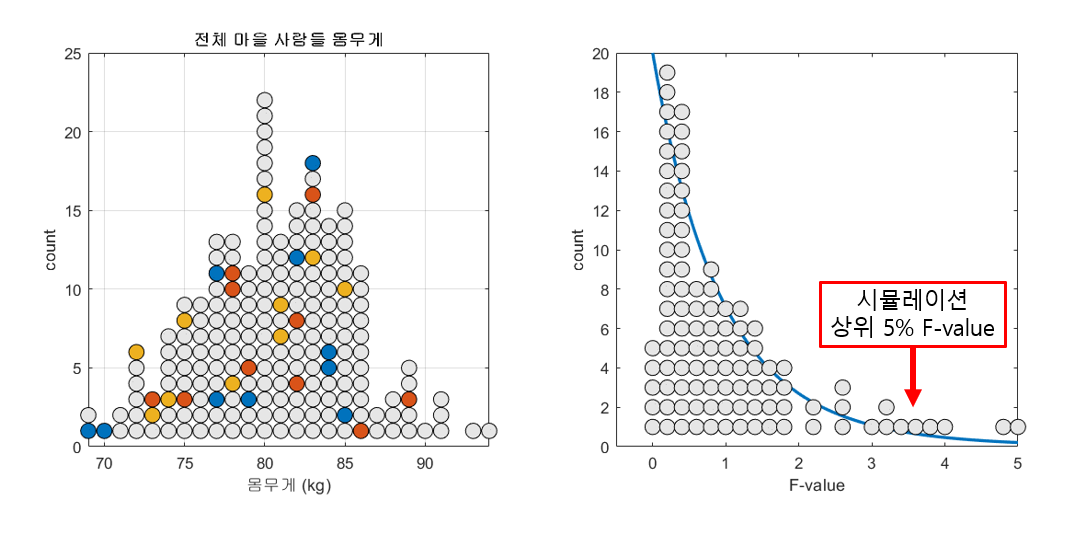
그림 5. 100회 F-value를 계산하는 시뮬레이션 결과 얻게 되는 상위 5% F-value
t-value와 F-value에 대한 증명: F = t^2
우리가 두 article에 걸쳐 확인한 t-value와 F-value는 사실상 같은 의미를 담고 있는 것이라고 강조했었다.
이번 꼭지에서는 $F=t^2$임을 수학적으로 확인해보고자 한다.
두 개의 표본 집단이 있고 각 표본의 크기는 $n$이며, 각 집단의 표본 평균과 표준 편차는 $\bar{X}_1$, $\bar{X}_2$와 $s_1$, $s_2$라고 하자.
먼저, F-value에서 사용하는 $s^2_{wit}$을 계산하면 다음과 같다.
\[s_{wit}^2=\frac{1}{2}(s_1^2+s_2^2)\]또, F-value에서 사용하는 $s^2_{bet}$을 계산하기 위해 다음과 같은 과정을 거칠 수 있다.
\[s_{\bar{X}} = \sqrt{\frac{(\bar{X}_1-\bar{X})^2+(\bar{X}_2-\bar{X})^2}{2-1}}\] \[\therefore s_{\bar{X}}^2=(\bar{X}_1-\bar{X})^2+(\bar{X}_2-\bar{X})^2\]여기서
\[\bar{X} = \frac{1}{2}(\bar{X}_1+\bar{X}_2)\]이므로,
\[식(15) = \left[\bar{X}_1-\frac{1}{2}(\bar{X}_1+\bar{X}_2)\right]^2 + \left[\bar{X}_2-\frac{1}{2}(\bar{X}_1+\bar{X}_2)\right]^2\] \[=\left(\frac{1}{2}\bar{X}_1 - \frac{1}{2}\bar{X}_2\right)^2+\left(\frac{1}{2}\bar{X}_2 - \frac{1}{2}\bar{X}_1\right)^2\]실수를 제곱해주면 항상 양수이므로 식 (18)의 두 항의 값은 같다. 따라서,
\[식(18) = 2\left(\frac{1}{2}\bar{X}_1 - \frac{1}{2}\bar{X}_2\right)^2\] \[=\frac{1}{2}\left(\bar{X}_1 - \bar{X}_2\right)^2\]따라서 $s^2_{bet}$은 다음과 같다.
\[s^2_{bet} = ns_{\bar{X}}^2=(n/2)\left(\bar{X}_1-\bar{X}_2\right)^2\]따라서, 이번 article에서 알아본 F-value의 정의에 따르면,
\[F=\frac{s^2_{bet}}{s^2_{wit}}=\frac{(n/2)(\bar{X}_1-\bar{X}_2)^2}{(1/2) (s_1^2+s_2^2)}\] \[=\frac{(\bar{X}_1-\bar{X}_2)^2}{(s_1^2/n)+(s_2^2/n)}\] \[=\left[\frac{\bar{X}_1-\bar{X}_2}{\sqrt{(s_1^2/n)+(s_2^2/n)}}\right]^2\]식 (24)의 괄호 내에 있는 값은 t-value와 같다. 따라서,
\[F=t^2\]이다.
참고문헌
- Primer of biostatistics 6th edition, Stanton A Glantz, McGraw-Hill Medical Publishing Division