고등학교 시절에 배우는 통계학에서는 중심극한정리에 대해 다음과 같이 설명하고 있다.

자연 현상이나 사회 현상 중에는 확률밀도함수의 그래프가 오른쪽 그림과 같이 어떤 값을 중심으로 대칭적으로 분포하며 중심에서 멀어질수록 도수가 작아지는 종 모양의 곡선에 가깝게 나타나는 경우가 많이 있다.

고등학교 수학 교과서 $\lt$확률과 통계$\gt$, 지학사, 2009

여기서 말하는 ‘오른쪽 그림’은 일반적인 정규분포의 형태를 그려놓은 그래프이다.

생각해보면 왜 이런 현상이 일어나는지에 대해 조금 더 자세히 말해주었다면 좋았을 것 같다는 생각이 많이 들게 하는 문장이다.

거기다가 아래와 같이 정규분포의 식은 복잡하기까지 하기 때문에 처음 배우는 입장에서는 거부감이 들 수 밖에 없다.

\[f(x) = \frac{1}{\sigma\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\]

중심극한정리의 핵심 키워드는 “평균”

중심극한정리에 대해 이해하기 위해선 표본의 평균을 추출하는 과정에 대해 잘 이해할 필요가 있다.

모집단에서부터 표본을 추출하는 과정을 잘 생각해보자.

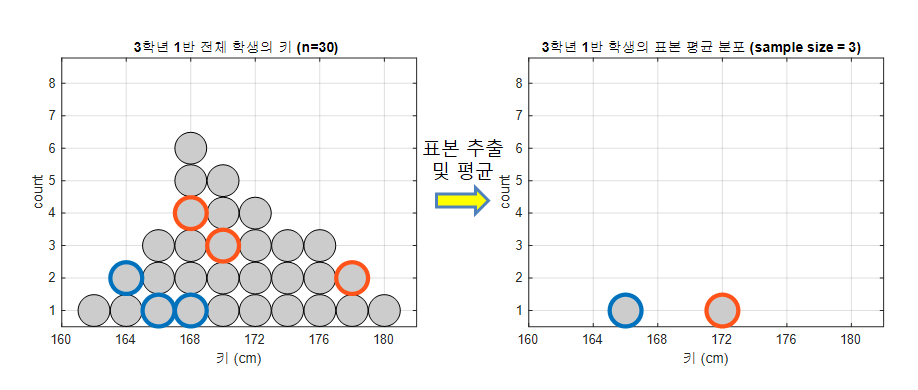
그림 1. 모집단에서 크기가 3인 샘플을 2회 추출하여 각 추출 시 마다 평균을 계산하여 histogram으로 표현한 것

보통은 모집단이라 하면 굉장한 대규모 집단에 대한 특성을 확인하지만 이번에는 이해를 돕고자 매우 작은 크기의 모집단을 생각해보자.

그림 1과 같이 3학년 1반 전체 학생의 키라는 특성에 대한 모집단을 생각해보자.

여기서 샘플을 추출한다는 것은 이 30명의 전체 학생 중에서 일부를 임의로(랜덤하게) 선택하겠다는 뜻이다.

또, 샘플 추출 시 필요한 과정이 하나 있다면 샘플의 크기를 정해주는 것인데, 이것은 연구자가 설정하기 나름이다. 그림 1의 경우에는 샘플의 크기가 3이 되도록 설정하였다.

그림 1의 좌측에서 볼 수 있듯이 한 번 샘플을 추출 할 때 마다 3명씩 랜덤하게 선택하였다.

또, 매 회 추출한 샘플들의 평균 키를 계산해 그림 1의 우측에 히스토그램 형식으로 표시할 수 있다.

가령, 파란색으로 표시한 데이터들의 경우에는 세 개의 값들이 추출되었는데, 164, 166, 168이 추출되었으므로 평균값은 166이다.

이 평균값은 그림 1의 우측에 histogram으로 파란색으로 표시하였다.

표본 추출을 무수히 많이 하면?

위의 꼭지에서는 표본 추출이 딱 두 번 시행되었다.

그런데, 표본 추출이 2회가 아니라 무수히 많이 수행되면 그림 1의 우측에서 본 것과 같은 표본 평균의 분포가 어떤 형태를 갖게 될까?

정답부터 말하자면, 표본 추출이 무수히 많이 되는 경우 비로소 표본 평균의 분포가 정규분포에 수렴하게 된다.

(여기서 주의할 점은 표본의 크기가 클 수록(즉, 한번 뽑을 때 많이 뽑을 수록) 표본 평균의 분포가 정규분포에 더 가깝게 수렴한다는 점이다.

표본 추출 횟수를 100회로 늘린 것은 Monte Carlo 방식으로 표본의 분포를 확인해보기 위함일 뿐이다.)

현실적으로 무한히 샘플 추출을 수행할 수는 없기 때문에 샘플 추출을 100번 시행해보도록 하자.

그림 2. 크기 3인 표본을 100회 추출하면서 매 회 추출된 표본의 평균값을 histogram 형태로 도시한 것

모집단의 모양에 상관없이 중심극한정리는 성립

한편, 그림 1과 2에서는 모집단의 형태가 정규분포의 형태와 유사했는데, 혹시 그래서 표본 평균의 분포가 정규 분포를 따르게 되는 것일까?

정답은 ‘그렇지 않다’이다.

중심극한정리가 강력한 이유는 모집단의 형태가 어떻든지 간에 상관없이 표본 평균의 분포는 정규분포를 따르게 된다는 점에 있다.

아래는 모집단이 그림 1 혹은 그림 2와 전혀 다른 형태의 분포를 가지는 경우의 표본 평균의 histogram 예시이다.

아래의 그림 3에서는 모집단의 분포가 uniform distribution을 따르는 경우를 상정하였다.

그림 3. 모집단의 분포가 uniform distribution인 경우 매 회 추출된 표본의 평균값을 histogram 형태로 도시한 것

요약

배운 내용을 요약하자면 다음과 같다.

• 표본 평균의 분포는 정규 분포에 근사하게 된다.
• 모집단의 모양이 어떻든 관계없이 중심극한 정리는 성립한다.
• 심지어는 표본을 추출하는 모집단이 서로 독립적이라면 여러 모집단에서 추출한 표본이더라도 표본 평균의 분포는 정규분포에 근사하게 된다¹.

그렇다면 처음에 교과서 내용에서 언급한 자연현상이나 사회현상에서 종모양의 분포가 자주 보이는 이유는 무엇일까?

필자의 사견으로는, 자연현상이나 사회현상들은 단독적인 특성만을 가지고 일어나는게 아니라 여러가지 특성들이 합쳐서 평균적인 결과로써 현상이 나오는것이기 때문에 그 현상은 이런 종모양을 따를 수 밖에 없지 않을까 생각한다.

그리고, 또 한가지 우리가 중심극한정리에 초점을 맞춰 통계학을 공부하게 되는 이유는 우리는 대체적으로 표본을 비교할 때 평균에 대한 비교를 많이 하기 때문에 이와 관련된 현상인 중심극한정리를 염두해두고 얻어진 이론들을 많이 접하게 되기 때문이다.