line integral을 할 때 어떤 벡터장은 path에 상관없이 같은 결과를 보여준다.
path independence의 결과는 그 벡터장이 어떤 스칼라 함수 $F$의 gradient 일 때 path-independent하다고 말한다.
그러한 결과는 미분적분학의 기본정리에 의해 당연히 그렇게 나와야 하는 결과이다.
이제부터 이 말의 의미가 무엇인지 알아보도록 하자.
증명 방식과 내용은 Khan academy의 Youtube 영상을 참고했다.
1. 보존장 (conservative field)
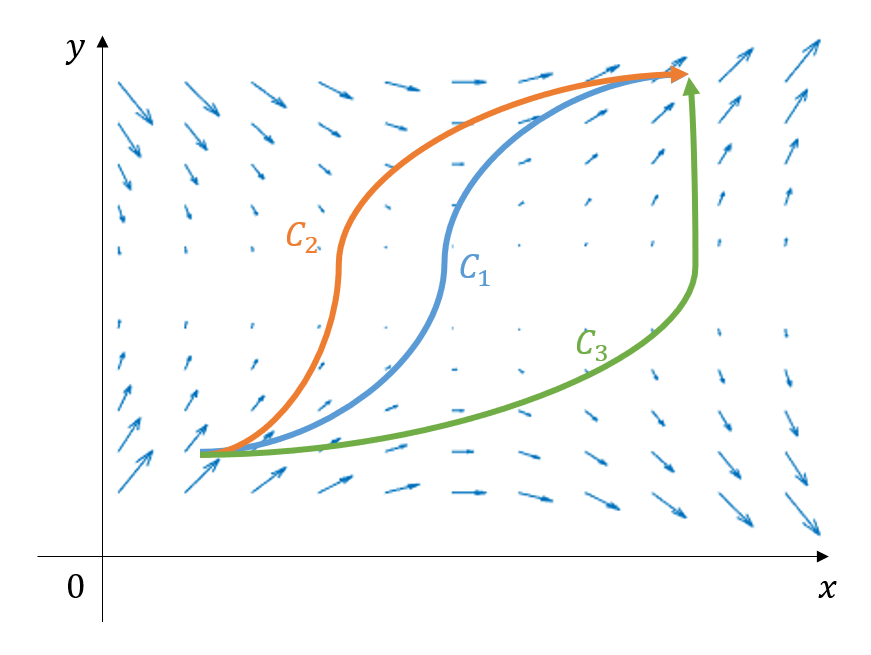
그림 1 어떤 벡터장에서 임의의 시작점과 끝점이 같은 세 curves, $C_1$, $C_2, $C_3$
그림 1에서 볼 수 있듯이 $xy$ 평면상에 어떤 벡터장이 있다고 해보자. 벡터장의 식은 다음과 같다.
(지금 당장은 벡터장의 식이 어떤지는 중요하지 않을 수 있다.)
\[f(x,y) = y^2\hat{i}+2xy\hat{j}\]이 때 이 벡터장은
\[\int_C\vec{f}\cdot d\vec{r} = \int_{C_2}\vec{f}\cdot d\vec{r} = \int_{C_3}\vec{f}\cdot d\vec{r}\]이면 보존장(conservative field)라고 한다.
즉, 경로에 관계없이 시작점과 끝점이 같은 서로 다른 경로를 선적분 해주었을 때 값이 같다면 보존장이라고 할 수 있다.
2. Multivariate chain rule
임의의 scalar 함수 $f(x(t),y(t))$에 대해 다음이 성립한다.
\[\frac{df}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt} + \frac{\partial f}{\partial y}\frac{dy}{dt}\]위의 chain rule이 말하는 것은 다음과 같다. 우리가 알고 싶은 것은 $t$가 조금씩 변할 때 $f$의 변화율이다.
그런데, $f$는 $x$와 $y$에 연관되어 있고 또 $x$와 $y$는 $t$에 연관되어 있으므로 위와 같은 관계가 형성되는 것이다.
3. 보존장의 조건 및 증명
어떤 벡터장이 보존장이 되기 위해서는 그 벡터장은 어떤 스칼라 함수의 gradient이어야 한다. 다시 말해,
\[\vec{f}(x,y) = \nabla F\] \[\text{where} \notag\] \[F = F(x,y)\]즉,
\[\vec{f}(x,y) = \frac{\partial F}{\partial x}\hat{i} + \frac{\partial F}{\partial y}\hat{j}\]일 때 이다.
증명은 아래와 같이 가능하다.
\[d\vec{r} = dx\hat{i} + dy\hat{j}\]이므로
\[\frac{d\vec{r}}{dt} = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}\]라고할 수 있다.
또 이로부터
\[d\vec{r} = \frac{dx}{dt}dt\hat{i} + \frac{dy}{dt}dt\hat{j}\]라고 적어도 무방하다.
이제, 벡터장 $\vec{f}$가 보존장인지 알아보자. 이 때, 매개변수 $t$의 범위는 $a\leq t \leq b$로 하자.
선적분 (line integral)을 하기 위해 $\vec{f}\cdot d\vec{r}$을 먼저 구해보자.
\[\vec{f}\cdot d\vec{r} = \left(\frac{\partial F}{\partial x}\hat{i} + \frac{\partial F}{\partial y}\hat{j}\right)\cdot \left(\frac{dx}{dt}dt\hat{i}+\frac{dy}{dt}dt\hat{j}\right)\] \[=\frac{\partial F}{\partial x}\frac{dx}{dt}dt + \frac{\partial F}{\partial y}\frac{dy}{dt}dt\]따라서 선적분은
\[\int_C\vec{f}\cdot d\vec{r} = \int_{t = a}^{t = b}\frac{\partial F}{\partial x}\frac{dx}{dt}dt + \frac{\partial F}{\partial y}\frac{dy}{dt}dt\] \[=\int_{a}^{b}\left(\frac{\partial F}{\partial x}\frac{dx}{dt} + \frac{\partial F}{\partial y}\frac{dy}{dt}\right)dt\]이다.
마지막의 식 (13)을 보면
\[\frac{\partial F}{\partial x}\frac{dx}{dt}+\frac{\partial F}{\partial y}\frac{dy}{dt}=\frac{dF}{dt}\]이므로 위의 선적분은 다음과 같이 쓸 수 있다.
\[\int_C\vec{f}\cdot d\vec{r} = \int_a^b\left(\frac{\partial F}{\partial x}\frac{dx}{dt} + \frac{\partial F}{\partial y}\frac{dy}{dt}\right)dt=\int_a^bdF = F(b) - F(a)\]따라서 보존장에서는 경로에 상관없이 시작점과 끝점이 일치하는 path들의 선적분은 같은 결과를 보여준다.
이것은 처음에 설명하였듯이 미분적분의 기본정리에 의한 것이라고 할 수 있다.