신호 공간(signal space)

Prerequisites

본 포스팅을 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오는 것이 좋습니다.

벡터의 기본 연산

signals as vectors

※ 이 꼭지의 내용은 이전 포스팅 중 선형 연산자와 신호 공간의 일부 내용을 가져다 썼습니다.

이전 포스팅 중 선형대수학의 기초 부분인 벡터의 기본 연산(상수배, 덧셈)에서는 세 가지 관점으로 벡터를 생각했다.

각각은 벡터란 화살표 같은 것, 숫자의 나열, 벡터 공간의 원소라는 정의였다.

그 중 벡터란 벡터 공간의 원소라는 정의가 가장 수학적인 정의라고 말한 바 있는데, 이 정의가 중요한 이유는 ‘이런 방식으로 벡터를 정의하는 것은 이러한 특성을 가진 것들은 모두 벡터로 취급해서 다룰 수 있다는 점을 강조한다’라고 언급했다.

다시 말해, 벡터의 특성을 가지는 개념을 발견한다면, 선형대수학에서 적용해볼 수 있었던 테크닉들과 개념들을 확장해 적용해볼 수 있게 되는 것이다.

조금 더 구체적으로 말하자면 어떤 수학적 object(가령, 벡터, 행렬, 신호, 등등…)가 벡터이기 위해선 다음의 두 가지 연산에 대해 닫혀있어야 한다.

벡터의 상수배
벡터의 합

너무 단순한가?

마치 쿠팡에서 로켓와우 멤버십 가입비 2900원만내면¹ 쿠팡에서 제공하는 모든 로켓배송 서비스를 누릴 수 있는 것 처럼, 어떤 수학적 object가 위의 두 개의 법칙만 잘 만족하는 것이라고 확인된다면 ‘벡터’라는 멤버십을 받게 되는 것이다.

그리고 이에 따라 선형대수학에서 열심히 일궈놓은 개념들과 테크닉들을 적용받을 수 있게 된다.

그림 1. 쿠팡에서 로켓와우 멤버십에 가입해 누릴 수 있는 혜택들 (출처: 쿠팡)

엄밀한 증명은 아니지만 간단하게만 생각해봐도 신호는 벡터로 볼 수 있는 자격을 갖췄다.

아래는 이산 신호의 상수배와 신호끼리의 합을 표현한 것이다.

\[(c\cdot x)[n] = c\cdot x[n] % 식 (1)\] \[(x+z)[n] = x[n]+z[n] % 식 (2)\]

다시 말해 어떤 신호 $x[n]$에 임의의 상수 $c$를 곱하더라도 여전히 $cx[n]$는 신호이고,

어떤 신호 $x[n]$과 $z[n]$를 더하더라도 $x[n]+z[n]$ 역시 신호다.

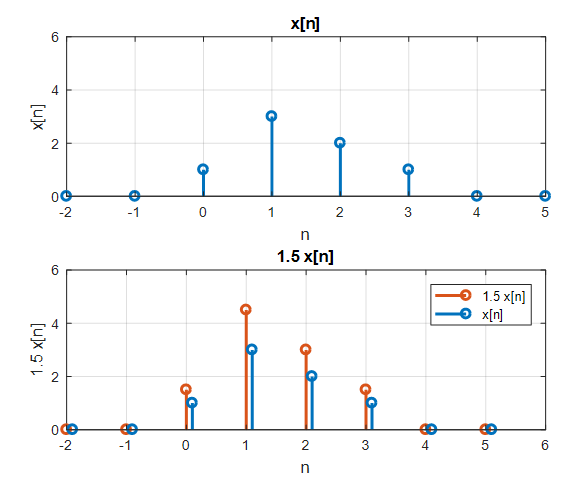
그림 2. 임의의 이산 신호에 상수배를 해주어도 여전히 이산 신호이다.

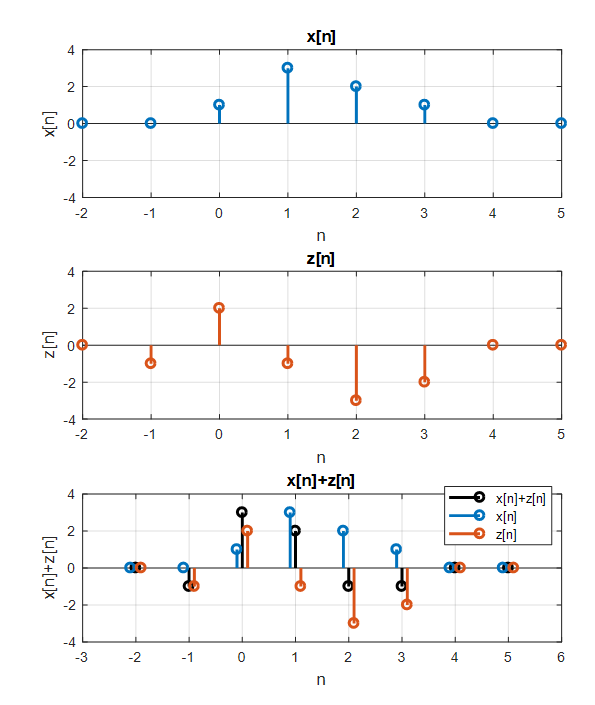
그림 3. 서로 다른 임의의 두 이산 신호를 더하더라도 여전히 이산 신호이다.

단순히 이산 신호 뿐만 아니라 연속 신호도 마찬가지로 상수배 혹은 신호끼리의 합을 수행하더라도 여전히 연속 신호로 남게 된다.

그림 4. 두 연속 신호의 합
그림 출처: Function space, Wikipeda

이렇게 되면 벡터가 벡터 공간의 원소로 정의되었던 것 처럼, 신호도 벡터 공간의 원소로 정의될 수 있는 벡터가 되며, 이 때 신호가 포함되어 있는 벡터 공간을 “신호 공간(signal space)”이라고 부른다.

우리는 벡터의 개념을 확장해서 신호 공간이라는 개념을 얻어낼 수 있음을 알게되었다.

이제 중요한 점은 어떻게 벡터에 적용되는 선형대수학의 개념들과 테크닉 중 어떤 것을 신호에 적용할 것인가 라는 점이다.

어떤 개념을 확장시키고자 할 때는 아주 기초적인 것들부터 의심해봐야한다. 벡터의 ‘좌표’ 라는 개념부터 의심해보는 것이 현명한 스타트라는 생각이 든다.

신호는 신호 공간 상의 한 점

벡터에 대해 생각할 때 가장 먼저 떠오르는 것 중 하나는 벡터란 화살표 같은 것이라는 정의이다. 벡터의 특징으로 ‘크기와 방향이 있다’ 이렇게 생각하는 경우가 많다.

이러한 벡터에 대한 정의는 Euclidean vector에 한정해서만 성립하기 때문에 아주 일반적인 벡터에 대한 정의라고 볼 수는 없지만 벡터에 대해 시각적으로 이해하는데에 큰 도움을 주는 방식의 정의라고 할 수 있다.

(다시 한번, 벡터이기 위한 요건은 스칼라배와 합이지 크기와 방향을 가져야 하는 것은 아니라는 점을 꼭 기억하자. 크기와 방향을 가지기 위해선 내적이 정의되어야만 한다.)

어찌되었든 우리는 2차원 공간 상의 한 점을 생각해보자. 좌표는 (3,4)라고 생각해보자.

여기서 우리가 좌표가 (3,4)인 벡터를 생각한다라고 하는 말은 어떤 2차원 벡터 공간 상의 기저 벡터 두 개를 몇 개씩 결합할것인가에 관한 표현을 간략화 한 것이다.

아래 그림은 좌표가 (3,4) 인 벡터와 2차원 벡터 공간 상의 기저벡터 두 개 $\hat{i}$와 $\hat{j}$를 표시한 것이다.

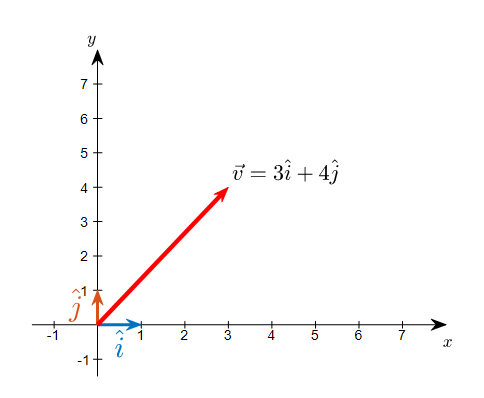
그림 5. 좌표가 (3,4)인 벡터와 표준기저벡터 $\hat{i}$와 $\hat{j}$

그리고 또 다른 아래의 그림에서는 (3,4) 좌표의 벡터가 기저벡터 3개, 4개를 각각 더해 구성할 수 있는 것임을 알 수 있다.

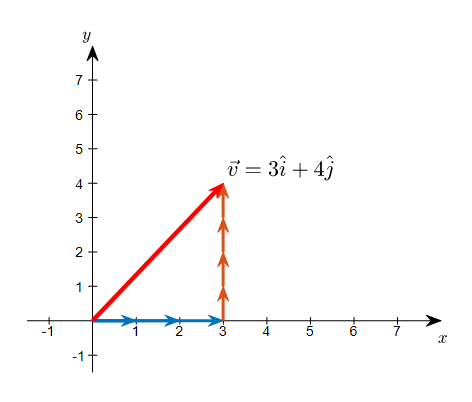
그림 6. 좌표가 (3,4)라는 말은 한 기저벡터 3개와 다른 기저벡터 4개의 합으로 그 벡터를 표현할 수 있다는 의미이다.

그러면 이 표준기저벡터들을 항상 사용해야하는것일까? 사실은 2차원 벡터 중 아무거나 두개를 골라서 기저벡터로 삼을 수 있다.

아래 그림은 좌표계를 반시계방향으로 10’ 회전시켜 만든 새로운 좌표계이다. 그리고 이 때의 기저벡터는 $\hat{i}{new}$와 $\hat{j}{new}$로 표시했다.

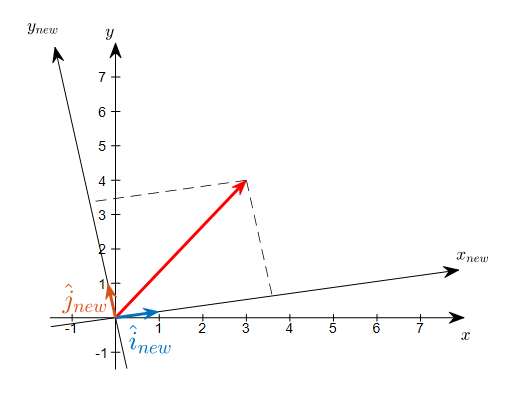
그림 7. 위에서 (3,4)로 표현했던 벡터에 대해 새로운 기저벡터가 적용되는 좌표계로 다시 이 벡터를 표현할 수 있을까?

새로운 기저벡터를 이용해 원래의 벡터를 표현하면 좌표는 (3.6, 3.4)이다. 이것은 기저벡터가 몇 개 들어가는지를 표시하는 것과 동일하다.

그림 8. 새로운 기저벡터를 이용하면 각각의 기저벡터를 3.6개, 3.4개 사용하여 원래의 벡터를 표현할 수 있다.

이처럼 벡터는 벡터 공간상의 한 점과 같다. 다만, 이 벡터를 표현할 수 있는 방법은 기저에 따라 바뀐다.

수식으로 쓰자면 임의의 벡터 $\vec{v}$는 기저벡터들의 선형결합으로 아래와 같이 쓸 수 있다.

\[\vec{v}=c_1 \hat{i} + c_2 \hat{j} = d_1 \hat{i}_{new} + d_2\hat{j}_{new}\]

어떤 기저는 다른 기저에 비해서 동일한 벡터를 표현하는데에도 표현이 단순해지고 간결해진다.

앞선 예시에서는 $c_1$과 $c_2$는 각각 3, 4로 단순했지만 $d_1$과 $d_2$는 3.6, 3.4로 조금 더 복잡해졌다.

이처럼 동일한 벡터 하나를 표현하는데 좋은 기저를 정하는 것은 매우 중요하다.

신호도 마찬가지로 임의의 신호를 기저 신호의 선형결합으로 표현할 수 있다.

임의의 신호 $x[k], k = 1, 2,\cdots n$이 포함되어 있는 신호 공간에 대한 기저 신호를 $\lbrace \phi_i[k] | i = 1,2,\cdots, n\rbrace$라고 잡는다면 임의의 신호 $x[n]$은 다음과 같이 기저 신호들의 선형결합으로 표현할 수 있다.

\[x[k]=\sum_{i=1}^{n}p_i \phi_i[k]\]

이는 연속 신호에 대해서도 마찬가지로 임의의 신호 $x(t)$가 포함되어 있는 신호 공간의 기저 신호를 $\lbrace \psi _i(t)\rbrace$라고 두면 이 신호는 다음과 같이 기저 신호들의 선형결합으로 표현할 수 있다.

\[x(t) = \sum_i q_i \psi_i(t)\]

한편, 하나의 벡터를 표현하기 위해 기저 벡터가 몇 개 들어갈지를 계산하는 방법은 ‘벡터의 내적’으로 알아볼 수 있다. 즉, 위 식들에서 $p_i$와 $q_i$를 계산하는 방법은 벡터의 내적처럼 신호의 내적을 정의해줌으로써 가능하다는 의미가 된다.

벡터 간의 내적 → 신호의 내적

선형대수학에서 벡터의 내적은 다음과 같이 정의되었다.

임의의 아래와 같은 $n$차원 실수 벡터 $\vec{a}$와 $\vec{b}$에 대하여,

\[\vec{a} = \begin{bmatrix}a_1\\ a_2 \\ \vdots \\ a_n\end{bmatrix} % 식 (6)\] \[\vec{b} = \begin{bmatrix}b_1\\ b_2 \\ \vdots \\ b_n\end{bmatrix} % 식 (7)\] \[\text{dot}(\vec{a}, \vec{b})=a_1b_1 + a_2b_2 +\cdots + a_nb_n % 식 (8)\]

만약 $\vec{a}$와 $\vec{b}$가 복소 벡터였다고 하면 내적은 다음과 같이 정의된다.

\[\text{dot}(\vec{a}, \vec{b})=a_1^*b_1 + a_2^*b_2 +\cdots + a_n^*b_n % 식 (9)\]

여기서 $*$은 복소 켤레(complex conjugate) 연산이다.

왜 복소 벡터는 복소 켤레 연산이 들어가는지 생각해본다면 내적을 통해 복소 벡터에서 길이를 정의하기 위해서이다.

어떤 실수 벡터 $\vec{a}$의 크기(보통 L2-norm)는 다음과 같이 정의된다.

\[\text{norm}_2(\vec{a}) = \sqrt{a_1^2 + a_2^2 + \cdots + a_n^2} % 식 (10)\]

즉,

\[\text{norm}_2(\vec{a}) = \sqrt{\text{dot}(\vec{a}, \vec{a})}=\sqrt{a_1a_1+a_2a_2+\cdots+a_na_n} % 식 (11)\]

이 개념을 복소벡터에까지 확장시키면, 복소 벡터 $\vec{a}$에 대해서

\[\text{norm}_2(\vec{a})=\sqrt{a_1^2+a_2^2 + \cdots a_n^2}=\sqrt{a_1^*a_1+a_2^*a_2+\cdots +a_n^*a_n}=\sqrt{\text{dot}(\vec{a},\vec{a})} % 식 (12)\]

이어야 하므로 복소벡터의 내적연산은 식 (9)과 같이 정의되어야 하는 것이다.

이제 식 (9)의 방식을 확장해 신호의 내적을 정의해보도록 하자.

신호들은 실수 신호 범위에서 그치지않고 신호값이 복소수가 될 수 도 있기 때문에 다음과 같이 복소 벡터의 내적의 정의를 확장해 다음과 같이 정의한다.

이산 신호의 경우 다음과 같이 정의된다. 임의의 복소 이산 신호 $x[k]$와 $z[k]$ $, k = 1, 2, \cdots, n$ 에 대하여

\[\langle x[k], z[k] \rangle \equiv \sum_{k=1}^n x[k]z^*[k]\]

이다. 여기서 $z^*[k]$는 $z[k]$의 complex conjugate이다.

또, 구간 $(a, b)$에서 정의된 임의의 복소 연속 신호 $x(t)$, $z(t)$에 대해 두 신호의 inner product $\langle f, g\rangle$은

\[\langle x(t), z(t)\rangle \equiv \int_a^b x(t)z^*(t) dt % 식 (10)\]

이다. 여기서 $z^*(t)$는 $z(t)$의 complex conjugate이다.

고유함수

고유함수에 관해 더 잘 이해하기 위해선 아래의 내용에 대해 알고 오는 것이 좋습니다.

고유함수에 대해 이해하게 되면 왜 신호/시스템 분야에서 신호를 복소 정현파를 이용해 서술하는지 알 수 있다.

지금까지의 논의에서 신호(즉, 함수)가 벡터라는 것에 관해 알아보았다. 그리고, 신호가 벡터라면 선형대수학에서 논의되고 개발된 용어들을 확장해 적용할 수 있고 선형대수학에서 개발된 메소드마저도 이용할 수 있다는 사실을 일부 확인했다.

선형대수학에서 아주 중요한 주제 중 하나인 고윳값과 고유벡터를 신호 처리에 관해서도 일부 적용해볼 수 있다.

고유벡터의 개념에 대해서 조금 더 잘 알기 위해선 벡터와 행렬의 관계에 대해 알아야 한다.

행렬은 벡터에 관한 함수라고 할 수 있다. 그리고, 행렬은 벡터를 입력 받아 또 다른 벡터를 출력하는 역할을 한다.

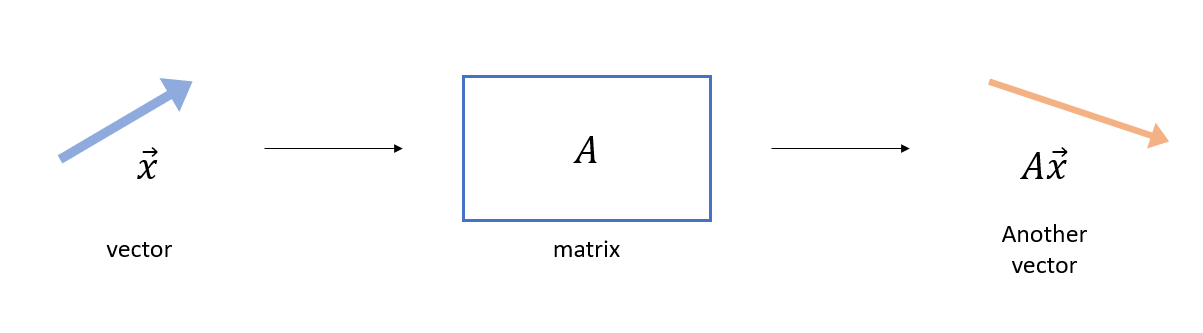
그림 9. 행렬은 벡터를 입력 받아 벡터를 출력해주는 함수이다.

이 때, 만약 어떤 행렬이 벡터를 입력 받아 출력했는데, 출력된 벡터가 입력된 벡터와 비교했을 때 크기만 바뀌고 방향은 그대로인 경우가 있을 수 있다.

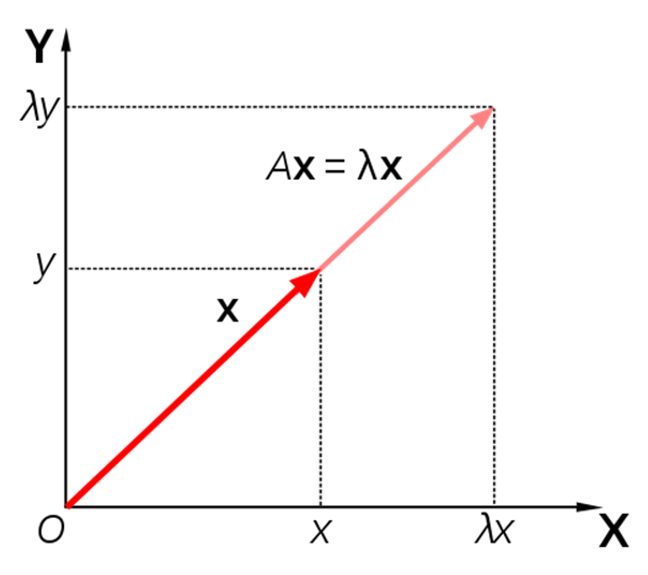
그림 10. 입력 벡터 ($x$)와 출력 벡터($Ax$)가 방향은 동일하고 크기만 차이나는 경우

이런 경우에 이 벡터 $x$의 방향으로 향하는 단위 벡터를 행렬 $A$에 대한 고유벡터라고 하고, 크기의 변화량을 고윳값이라고 부른다.

그런데, 우리가 공부하는 신호 시스템에서는 어떨까? 신호가 벡터라고 한다면 시스템은 행렬에 대응하는 것이다.

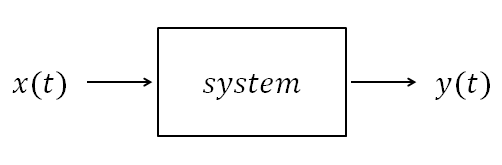
그림 11. 신호가 벡터에 대응되는 개념이라면 시스템은 행렬에 대응되는 개념이다.

그렇다면 우리가 다루는 시스템도 고유벡터에 대응하는 개념이 있을까?

신호, 시스템에서 고유벡터에 대응되는 개념을 우리는 보통 고유함수(eigenfunction)이라고 부른다. (고유 신호라고는 보통 부르지 않음.)

보통 가장 중요하게 다루는 선형시불변(Linear Time-Invariant) 시스템에서는 복소 정현파가 고유함수가 된다.

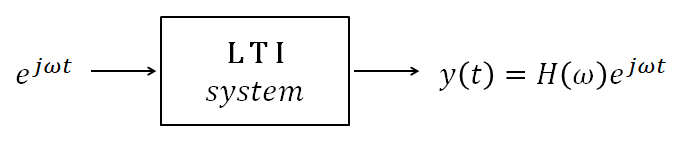
그림 12. LTI system에서는 복소 정현파가 고유함수가 된다.

조금 더 자세하게 보면, 입력이 $x(t)=e^{j\omega t}$ 이고 시스템의 impulse response가 $h(t)$라고 하면 출력은

\[y(t) = \int_{-\infty}^{\infty}e^{j\omega (t-\tau)}h(\tau)d\tau\] \[=e^{j\omega t}\int_{-\infty}^{\infty}h(\tau)e^{-j\omega\tau}d\tau\]

와 같다. 여기서 $H(\omega)$를 아래와 같이 정의하였는데, 이것은 $h(t)$의 푸리에 변환이라고 부르는 것이다.

\[H(\omega) = \int_{-\infty}^{\infty}h(\tau)e^{-j\omega\tau}d\tau\]

중요한 것은 원래의 식을 다시 써보면,

\[y(t)=H(\omega)e^{j\omega t}\]

가 되는데, 출력 함수를 보면 원래의 입력 함수 $e^{j\omega t}$가 그대로 들어있고 그것에 $H(\omega)$이 곱해져서 출력되는 것을 알 수 있다.

생각해보면 너무 자연스럽게 $e^{j\omega t}$가 나오다보니 이게 뭐가 그렇게 특별한가 싶을지도 모르지만, 이번엔 코사인 함수를 입력으로 넣어보자.

코사인 함수는 오일러 공식에 의해 다음과 같이 수정해서 쓸 수도 있다.

\[x(t) = \cos(\omega t)=\frac{1}{2}(e^{j\omega t}+e^{-j\omega t})\]

시스템을 $\mathfrak L$이라고 하면, 우리의 시스템은 선형 시스템이기 때문에 다음이 성립한다.

\[y(t) = (\mathfrak{L}x)(t)=\frac{1}{2}\left(\mathfrak{L}(e^{j\omega t} + \mathfrak{L}(e^{-j\omega t})\right)\]

여기서 복소수 표현을 이용해 $H(\omega)$를 표현하면,

\[H(\omega) = |H(\omega)|e^{j \angle H(\omega)}\] \[H(-\omega) = H^*(\omega) = |H(\omega)|e^{-j\angle H(\omega)}\]

이므로, $y(t)$를 다시 쓰면 다음과 같을 것이다.

\[y(t) = \frac{1}{2}|H(\omega)|\left(e^{j(\omega t +\angle H(\omega))} + e^{-j(\omega t +\angle H(\omega))}\right)\] \[=|H(\omega)|\cos(\omega t + \angle H(\omega))\]

와 같다.

따라서, 코사인 함수를 입력으로 넣어주면 시스템에 의해 크기가 $|H(\omega)|$만큼 커질 뿐만 아니라 위상도 $\angle H(\omega)$만큼 shift되어 표현해주어야 한다.

그러므로 코사인 함수를 입력으로 넣어줬을 때는 출력에 원래의 입력이 그대로 출력되지 않으므로 코사인 함수는 선형 시스템에 대한 고유함수가 아니다.

여기서 알 수 있는 사실은 신호/시스템 분야에서는 신호를 표현할 때 복소 정현파를 이용해서 표현하며, 그 이유는 복소 정현파를 이용해 입력을 표현해주면 출력에는 시스템의 특성(임펄스 함수의 푸리에 변환)만 서술해주면 되어서 출력에 관한 서술이 간결해지기 때문이다.

참고 문헌

지금은 회비가 좀 올랐다. ↩

이전연속 시간 컨볼루션

다음푸리에 급수(Fourier Series)