푸리에 급수가 말하는 것: 임의의 주기함수는 삼각함수의 합으로 표현될 수 있다.

Prerequisites

이번 포스팅을 더 잘 이해하기 위해서는 아래의 내용에 대해 알고 오는 것이 좋습니다.

• 신호 공간(signal space)
• 미분방정식을 이용한 오일러 공식 유도
• 오일러 공식의 기하학적 의미

쉽게 설명해보는 푸리에 급수

세 종류의 장난감 블록이 있다고 생각해보자. 이 때, 세 종류의 블록은 생김새가 아주 다르게 생겼다는 것에 초점을 맞추자.

그림 1. 세모, 동그라미, 별표 모양의 장난감 블록을 상상해보자.

그리고 장난감 블록들이 마구잡이로 어지럽혀져 있다고 해보자. 우리가 하고자 하는 것은 이 장난감 블록들을 블록 모양별로 각 상자에 담아 넣는 것이다. 이걸 한번에 처리해줄 수 있는 방법이 있을까?

그림 2. 장난감 블록들을 한번에 치울 수 있는 방법은 없을까?

물론 마법으로 처리해버리면 좋겠지만, 우리에게는 마법능력이 없으니 … 이런 아이디어는 어떨까? 모든 장난감을 한번에 들이붓는데, 장난감 모양에 딱 맞는 필터가 있어서 이 구멍을 통과하게끔 만들면 각 블록 모양의 상자에 맞게 블록을 넣을 수 있게 되는 거라는 아이디어다.

그림 3. 장난감 블록들을 모양별로 걸러낼 수 있는 필터가 있다면 정리하기가 좀 편할 수도 있겠다.

갑자기 왜 블록과 필터 타령이냐고 할 수도 있겠지만, 이런 아이디어가 푸리에 급수(혹은 변환)가 갖고 있는 핵심 아이디어이기 때문이다.

푸리에 급수(혹은 변환)이란 간단하게 말해 여러 주파수 성분을 담고 있는 신호를 각 주파수 성분별로 분해해주는 역할을 하는 것이다. 이런 과정을 푸리에 해석 혹은 푸리에 분석이라고들 부른다.

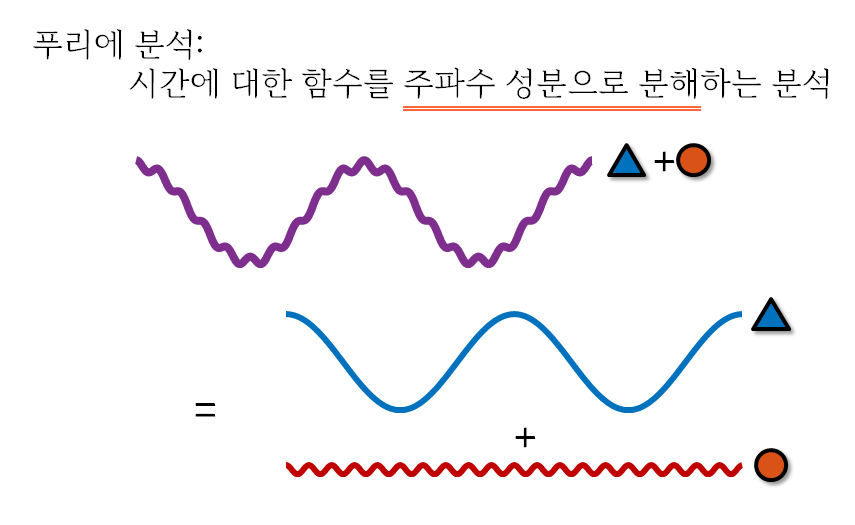
그림 4. 푸리에 분석(해석)의 핵심은 여러 주파수 성분을 담고 있는 신호를 각 주파수 성분별로 분해해주는 것이다.

그리고 이렇게 얻은 주파수 성분들을 시간 축이 아닌 주파수 축에 표현해주는 것을 (주파수) 스펙트럼을 표현한다고 말한다.

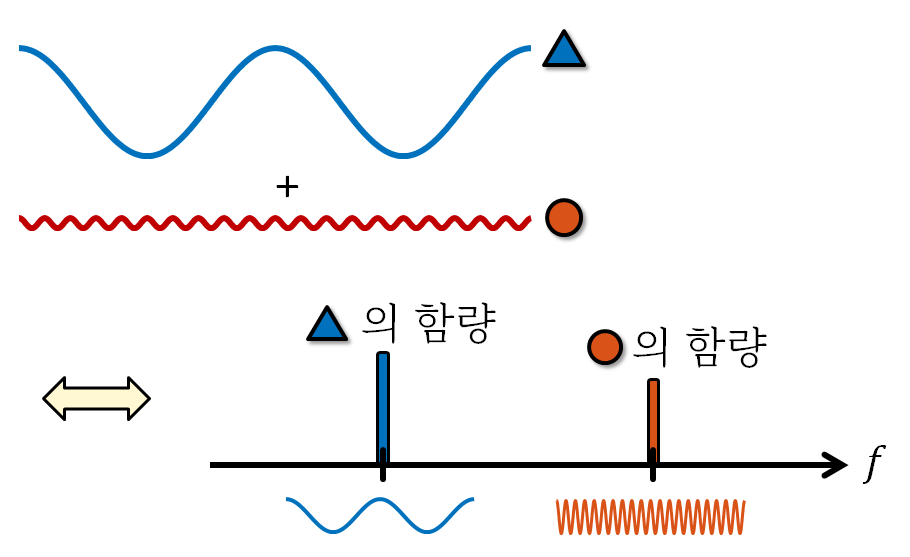
그림 5. 푸리에 분석(해석)의 핵심은 여러 주파수 성분을 담고 있는 신호를 각 주파수 성분별로 분해해주는 것이다.

푸리에 급수를 수행할 때는 분석하고자 하는 주기 신호의 가장 큰 주기(혹은 가장 낮은 주파수)를 확인하고 그 주파수의 정수배가 되는 정현파들을 미리 준비해둔다.

그래서 ‘내적(inner product)’을 이용해 각 정현파들과 닮은 정도를 계산하여 각 주파수 성분이 얼마만큼 들어있는지를 검사하는 과정인 것이다.

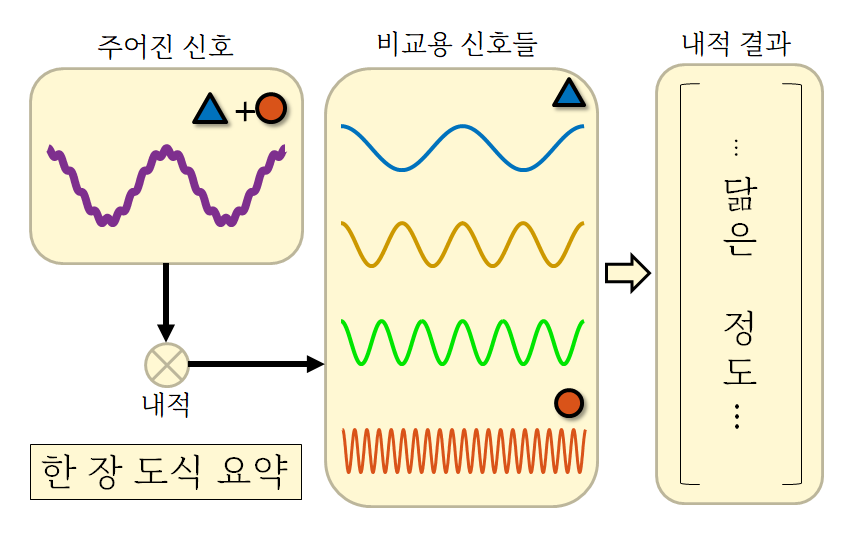
그림 6. 푸리에 분석(해석)을 한장으로 요약하면 미리 준비한 서로 다른 주파수를 가지는 정현파들과 내적과정을 통해 각 주파수 함량을 검사하는 방법이다.

이런 푸리에 분석이 유용한 이유 중 하나는 우리가 주파수 스펙트럼 상에서 신호를 분석할 수 있다면, 원하지 않는 특정 주파수 성분을 제거하는 것이 수월해질 수 있기 때문이다.

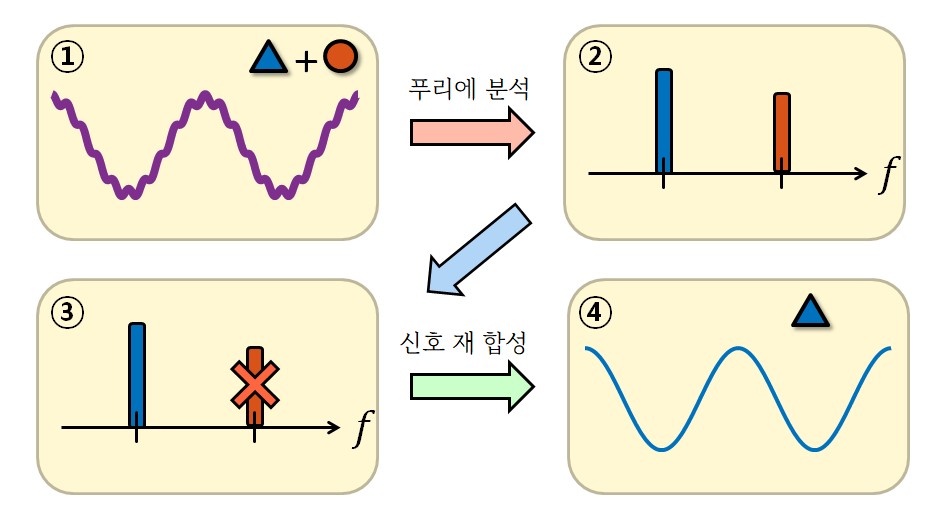
그림 7. 푸리에 분석(해석)이 유용한 이유: 주파수 스펙트럼 상에서 신호를 분석할 수 있으며, 원치 않는 주파수 성분을 제거해주는 것도 가능해지기 때문.

푸리에 급수의 유도 과정

앞서 비유를 들어 간단하게 설명한 푸리에 분석 중 푸리에 급수에 대해 수학적으로 (진지하게) 유도해보자.

기저 신호의 선택과 스펙트럼 표현

좌표 평면 상에 존재하는 $(3,4)$라는 벡터는 두 개의 서로 다른 기저벡터의 선형결합으로 표현될 수 있다는 것을 간략화하여 표기한 것과 같다.

\[(3,4) \Longleftrightarrow 3 \hat{i}+4\hat{j}\]

이전 포스팅 중 신호 공간(signal space) 편에서는 신호가 일종의 벡터로 생각될 수 있다고 언급했다.

임의의 벡터가 기저벡터들의 선형 결합으로 표현할 수 있는 것 처럼 임의의 신호는 기저 신호(basis signals)의 선형결합으로 표현될 수 있다.

임의의 연속 신호 $x(t)$에 대해 기저 신호가 $\lbrace \psi_i(t)\rbrace$라고 하면 다음과 같이 기저 신호들의 선형 결합으로 표현할 수 있다.

\[x(t)=\sum_i c_i \psi_i(t)\]

생각해보면 우리가 적절히 얻어낸 $\lbrace \psi_i(t)\rbrace$를 알고만 있다면 $c_i$를 구하는 것 만으로 $x(t)$를 표현할 수 있게 되는 것이다.

예를 들어 임의의 연속 신호 $x(t)$와 기저 신호 집합 $\lbrace \psi_i(t)\rbrace$에 대해 $i=1$일 때 $c_1=1$이고 $c_2=3$이라고 하자. 그 외의 $c_i=0$이라고 해보자.

그러면 이 신호는 다음과 같이 $c$ 축 위에 기저 신호의 성분량만을 표시해주면 충분하다.

이처럼 기저 신호의 성분량만을 이용해 원 신호를 표현해주는 방법을 스펙트럼 표현이라고 부른다.

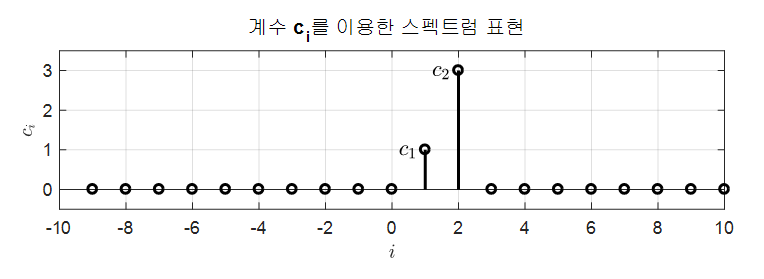
그림 8. 임의의 연속 신호 $x(t)$에 대한 스펙트럼 표현

---

신호 처리에 있어서 적절한 기저 신호는 어떤 특성을 만족해야 할까? 특별히 정해진 규칙은 없지만 한 참고문헌¹에서는 아래와 같이 특성을 제시하고 있다.

1. 형태가 단순하고, 신호의 표현을 구하기 쉬워야 한다.
2. 다양하고 폭넓은 신호들을 표현할 수 있어야 한다.
3. 표현된 신호에 대한 시스템의 응답을 편리하게 표기할 수 있어야 한다.
4. 한 주파수에 대해 오직 하나의 기본 신호만 존재(일대일 대응)해야 한다.

그리고 이러한 네 가지 특성을 가장 잘 만족하는 기저함수 중 하나가 삼각함수²이다.

그런데, 삼각 함수는 주기 함수이기 때문에 삼각 함수를 기저 신호로 하여 선형결합해 신호를 표현하기 위해선 표현해주고자 하는 신호가 주기함수여야 한다.

푸리에의 결과에 따르면 주기 신호는 같은 주기를 갖는 정현파와 이 정현파의 정수배의 주파수를 갖는 정현파의 합으로 표현할 수 있기 때문에³, 주기가 $T$인 임의의 연속 신호 $x(t)$를 다음과 같이 정현파의 선형결합으로 표현할 수 있다.

\[x(t)=a_0+\sum_{k=1}^\infty a_k\cos\left(\frac{2\pi k t}{T}\right)+\sum_{k=1}^{\infty} b_k \sin\left(\frac{2\pi k t}{T}\right)\]

여기서 수식의 형태를 단순화 시키고⁴(위의 조건 중 1번) 시스템 응답을 편리하게 표기하기 위해⁵(위의 조건 중 3번) 실수 정현파가 아니라 복소 정현파를 사용하자.

복소 정현파는 다음과 같이 오일러 공식을 가지고 얻게 된다.

\[\exp(j\theta) = \cos(\theta) + j \sin(\theta)\]

여기서 $j=\sqrt{-1}$이다.

그러므로,

\[\cos(\theta) = \frac{\exp(j\theta)+\exp(-j\theta)}{2}\] \[\sin(\theta) = \frac{\exp(j\theta)-\exp(-j\theta)}{2j}\]

와 같다는 것을 알 수 있기 때문에 $x(t)$를 다시 써보면 다음과 같다.

\[x(t)=a_0+\sum_{k=1}^\infty a_k\cos\left(\frac{2\pi k t}{T}\right)+\sum_{k=1}^{\infty} b_k \sin\left(\frac{2\pi k t}{T}\right)\] \[=a_0+\sum_{k=1}^{\infty}\left( a_k\frac{\exp\left(j 2\pi k t/T\right)+\exp\left(-j2\pi k t/T\right)}{2} + b_k\frac{\exp\left(j 2\pi k t/T\right)-\exp\left(-j 2\pi k t/T\right)}{2j} \right)\] \[=a_0+\sum_{k=1}^{\infty}\left( \frac{a_k-jb_k}{2}\exp\left(j\frac{2\pi k t}{T}\right)+\frac{a_k+jb_k}{2}\exp\left(-j\frac{2\pi kt}{T}\right) \right)\] \[=\sum_{k=-\infty}^{\infty}c_k\exp\left(j\frac{2\pi k t}{T}\right)\]

여기서 $c_k$는 $a_0, a_k, b_k$와 다음과 같은 관계를 갖는다고 볼 수 있다.

\[c_k = \begin{cases}\frac{1}{2}(a_k-jb_k),&& k >0 \\ a_0, && k = 0\\ \frac{1}{2}(a_k+jb_k), && k < 0 \end{cases}\]

결론적으로 우리는 복소 삼각함수를 이용해 임의의 연속 신호 $x(t)$를 표현할 수 있다.

복소 정현파의 직교성

특별히 삼각함수가 기저 신호로써 유용한 이유는 서로 다른 주파수의 삼각 함수 끼리는 직교하는 성질을 보여 신호의 표현을 구하기 쉬워지기 때문이다.

여기서 신호가 직교한다는 것은 신호 간의 내적이 0임을 의미하는데, 구간 $(a, b)$에서 정의된 임의의 신호 $x(t)$와 $z(t)$에 대해 다음이 성립하면 두 신호는 직교한다고 표현한다.

\[\lt x(t), z(t) \gt = \int_{a}^{b}x(t)z^*(t) dt= 0\]

가령, 구간 $(0, T)$에서 정의된 복소 정현파 두 개의 내적을 생각해보자.

\[\lt \exp\left(j\frac{2\pi k t}{T}\right), \exp\left(j\frac{2\pi p t}{T}\right)\gt\] \[=\int_{0}^{T}\exp\left(j\frac{2\pi k t}{T}\right)\exp\left(-j\frac{2\pi p t}{T}\right)dt\] \[=\int_{0}^{T}\exp\left(j\frac{2\pi (k-p) t}{T}\right)dt\]

여기서 $k=p$ 인 경우에는

\[\Rightarrow \int_{0}^{T}\exp(0)dt = T\]

반면 $k\neq p$인 경우에는 $q=k-p$로 치환하여

\[\Rightarrow \int_{0}^{T}\exp\left(j\frac{2\pi q t}{T}\right)dt\] \[= \frac{T}{j2\pi q}\left|\exp\left(j\frac{2\pi q t}{T}\right)\right|_{0}^{T}=\frac{T}{j2\pi q}(\exp(j2\pi q) - \exp(0)) = \frac{T}{j2\pi q}(1-1) = 0\]

이므로 서로 다른 주파수를 갖는 복소 정현파끼리는 서로 직교한다는 사실을 알 수 있으며, 같은 주파수를 갖는 복소 정현파끼리는 내적한 결과가 $T$와 같다는 것을 알 수 있다.

계수 $c_k$의 계산

한편 식 (10)에서부터,

\[x(t)=\sum_{k=-\infty}^{\infty }c_k \exp\left(j\frac{2\pi k t}{T}\right)\]

임을 알 수 있다.

이 때, $c_k$를 구하기 위해 다음과 같은 내적을 취해보면,

\[\lt x(t), \exp\left(j\frac{2\pi p t}{T}\right)\gt\] \[=\int_{0}^{T}x(t)\exp\left(-j\frac{2\pi p t}{T}\right)dt\] \[=\int_{0}^{T}\sum_{k=-\infty}^{\infty}c_k\exp\left(j\frac{2\pi kt}{T}\right)\exp\left(-j\frac{2\pi pt}{T}\right)dt\] \[=\int_{0}^{T}\sum_{k=-\infty}^{\infty}c_k\exp\left(j\frac{2\pi (k-p)t}{T}\right)dt\]

식 (16)과 식 (18)의 결과를 생각해보면

\[\Rightarrow c_k T\]

이다.

따라서, 계수 $c_k$는 다음과 같이 계산할 수 있다.

\[c_k =\frac{1}{T}\int_{0}^{T}x(t)\exp\left(-j\frac{2\pi k t}{T}\right)dt\]

요약

푸리에 급수에 대해 요약하면 다음과 같이 두 개의 수식으로 쓸 수 있다.

구간 $(0, T)$에서 정의된 $T$를 주기로하는 연속 신호 $x(t)$에 대해,

\[x(t)=\sum_{k=-\infty}^{\infty}c_k\exp\left(j \frac{2\pi k t}{T}\right)\] \[c_k = \frac{1}{T}\int_{0}^{T}x(t)\exp\left(-j\frac{2\pi k t}{T}\right)dt\]

예제

문제 1. 다음의 사각 펄스의 푸리에 급수를 계산하시오.

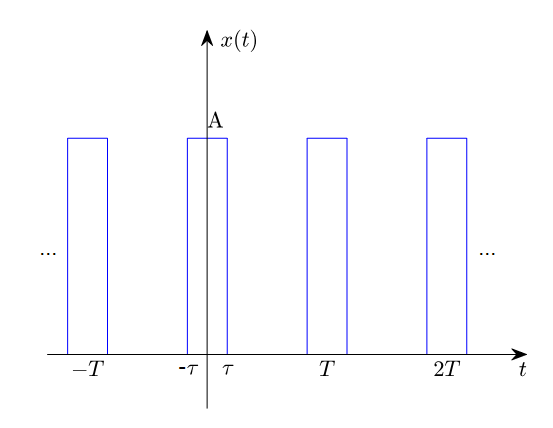
그림 9. 문제 1의 사각 펄스 주기 신호

위 그림을 보면 적분 주기를 $(-T/2, T/2)$로 두고 적분하면 한 주기에 대해 적분하면서도 함수가 끊기지 않고 적분할 수 있다는 것을 알 수 있다.

따라서, 푸리에 급수의 $c_k$는 다음과 같이 계산할 수 있다.

\[c_k = \frac{1}{T}\int_{-\tau}^{\tau}A\exp\left(-j\frac{2\pi k t}{T}\right)dt=\frac{A}{T}\left(-\frac{T}{j2\pi k}\right)\left|\exp\left(-j\frac{2\pi k t}{T}\right)\right|_{-\tau}^{\tau}\] \[=\frac{A}{T}\frac{T}{(-j2\pi k)}\left\lbrace\cos\left(\frac{2\pi k\tau}{T}\right)-j\sin\left(\frac{2\pi k\tau}{T}\right)-\cos\left(\frac{2\pi k\tau}{T}\right)-j\sin\left(\frac{2\pi k\tau}{T}\right)\right\rbrace\] \[=\frac{A}{T}\frac{T}{2\pi k}2\sin\left(\frac{2\pi k \tau}{T}\right)\]

여기서 사인함수를 sinc 함수로 맞춰주기 위해서 아래와 같이 두 번째 분수의 분자분모에 $\tau$를 곱하자.

\[=\frac{A}{T}\frac{T\tau}{2\pi k\tau}2\sin\left(\frac{2\pi k \tau}{T}\right)\] \[=\frac{2A\tau}{T}\text{sinc}\left(\frac{2k\tau}{T}\right)\]

여기서 sinc 함수는 다음과 같은 함수이다.

\[\text{sinc}(x)=\frac{\sin(\pi x)}{\pi x}\]

sinc 함수의 형태는 다음과 같다.

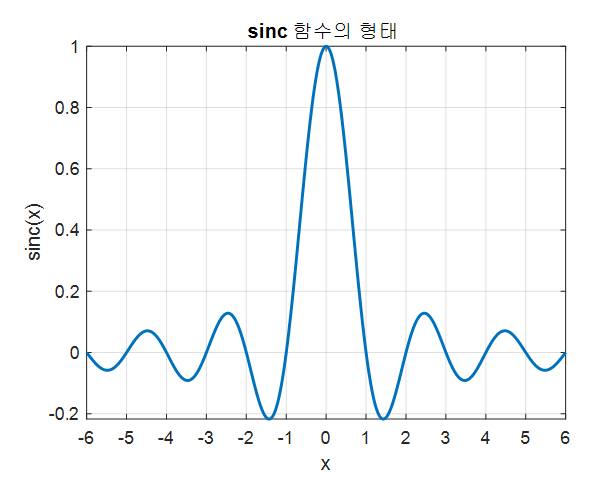
그림 10. 사각 펄스 주기 신호의 푸리에 계수(스펙트럼), $T = 3, \tau = 0.5, A = 2$ 인 경우

계수를 구했으니 원래의 신호 $x(t)$를 다음과 같이도 표현할 수 있음을 알 수 있다.

\[x(t) = \sum_{k=-\infty}^{\infty}c_k\exp\left(j\frac{2\pi k t}{T}\right)=\frac{2A\tau}{T}\sum_{k=-\infty}^{\infty}\text{sinc}\left(\frac{2k\tau}{T}\right)\exp\left(j\frac{2\pi k t}{T}\right)\]

위의 형태는 $k=0$일 때부터 $k=\pm 1$, $k=\pm 2$ 일 때 하나씩 더해가면서 얻게 되는 급수의 형태이다.

이를 컴퓨터를 이용해 그려보면 $k$가 변해감에 따라 원래의 그림 2의 사각 펄스 신호와 같은 형태를 띄게 되는 것을 알 수 있다.

그림 11. 푸리에 급수의 합을 계속해서 더해가면 원래의 펄스 주기 신호와 유사해진다.

한편, $c_k$를 $k$의 변화에 따라 그리면 다음과 같다. sinc 함수의 형태를 그대로 띄게 되며, 띄엄 띄엄 샘플되어 있는 형태를 볼 수 있다.

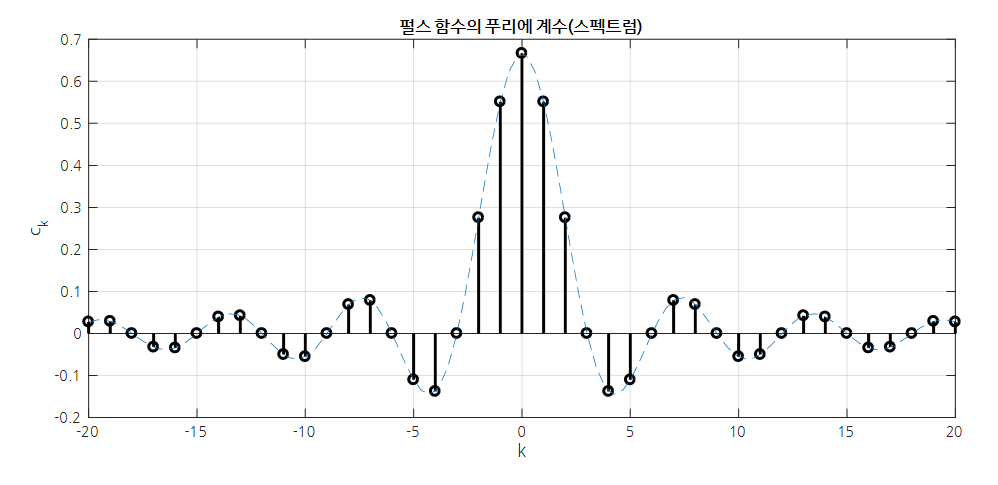
그림 12. 사각 펄스 주기 신호의 푸리에 계수(스펙트럼), $T = 3, \tau = 0.5, A = 2$ 인 경우

참고 문헌

• 디지털 신호 처리, 이철희, 한빛아카데미