1. 수의 발견

우리는 허수의 개념에 대해서 생각해보기 전에 앞서, 수의 체계에 대해서 생각해볼 필요가 있다. 일반적으로 수의 체계는 다음과 같이 알려져 있다.

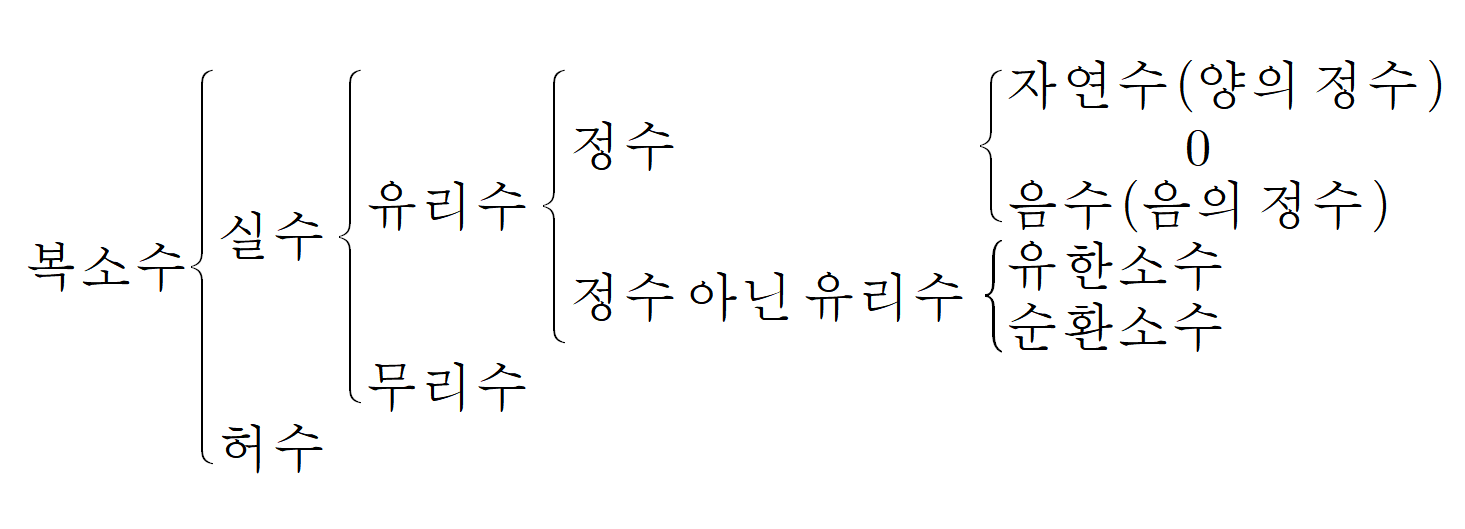
위 diagram은 복소수를 실수와 허수로 나누고, 실수를 유리수와 무리수로 나누는 방식 즉, top-down 방식으로 수의 체계를 서술했지만 원래대로라면 수는 자연수의 발견에서부터 출발했을 것이다. 즉, 처음 발견된 수 체계는 자연수였을 것이다.

그러니까 가령, 양 두 마리와 개 두 마리는 같은 두 마리라는 사실을 발견했을 것이다. 이것은 재산을 보호하기 위한 보안 수단으로 이용되었을 것이다.

자연수가 발견된 이후에는 아마 양의 유리수의 개념이 발견되지 않았을까 생각한다. 즉, ‘양이 1마리 2마리가 있지 1.5마리는 없지 않느냐?’는 질문에 대한 답변을 그 누군가 찾았을 것이다. 하지만 지금은 유리수의 개념이 매우 유용하게 쓰인다는 것은 모두가 알고있는 사실이다.

이러한 수 체계의 발견의 과정을 거듭하다보면 음수의 개념이 발견되었을 것인데, 음수의 개념은 처음에는 어렵고 상당히 쓸모없게 여겨지는 개념이었을 수도 있다고 생각한다. 왜냐면 음수의 개념은 양의 정수 입장에서 보았을 때, 수의 체계가 눈에 보이지 않는 수의 개념까지 확장되었기 때문일 것이다. 하지만 현 시대에 사는 모든 사람들은 음수의 개념이 ,특별히 설명하지 않더라도, 얼마나 유용한지 나도 모르는 사이에 깨닫고 있을 것이다.

2. 곱셈이 갖는 의미의 확장

곱셈은 덧셈을 여러 번 해준 것이지만, 음수 개념의 도입은 곱셈의 원래 의미에 위치 전환의 의미가 확장됨. 제곱은 곱셈의 패턴 반복.

이러한 음수의 체계는 곱셈이 가지는 의미를 확장시켰다고 할 수 있다. 결론적으로 말하자면 곱셈은 숫자를 방향성을 가지고 변환시킨다는 의미를 갖게 된다. 이게 왜 그런지 다시 한 번 생각해보자.

곱셈 연산은 1이라는 숫자로부터 어느 방향으로 몇 배만큼 키워주느냐는 말을 수식으로 표현한 것이다. 다시 한 번 말하자면, $1\times3$의 의미는 1이라는 숫자를 양의 방향으로 1이라는 수의 크기를 3배 크게 해주겠다는 의미이다. 그렇다면, 이 양의 방향이라는 것은 음의 방향과 대조되는 의미로 사용되었다는 것 또한 알 수 있다. 그렇기 때문에 다시 한 번, $-3$은 $1\times (-1) \times 3$으로 분리해 생각될 수 있으며, 이 수식은 1이라는 숫자를 음의 방향(-1)으로 3배 만큼 크게 해주겠다는 의미이다. 두 수식, $1\times 3$과 $1\times (-1)\times 3$을 보면 지금까지 없었던 방향의 개념(-1)이 표현되어있다는 것을 알 수 있다.

그러니까 곱셈의 의미는 음수의 체계를 발견함으로써 일방향성에서 양방향성으로 그 변환의 범위가 확장되는 것이다. 이제 방향이라는 말을 계속 사용한다는 것은 무엇을 말하고자 하는지 이해한 사람도 있을 것이다. 즉, 수의 개념은 이제 벡터의 개념으로 확장될 수 있는 것이다. 음의 수 체계의 발견은 한 방향으로만 정의되어 있던 ‘수’라고 알려진 스칼라를 1차원 벡터로 확장시켰다는 의미를 갖는 발견인 것이다.

3. 허수의 발견

실수의 차원을 벗어난 수. 허수는 회전이다.

허수는 다음과 같은 질문에 답하기 위해서 만들어진 수의 개념일 것이다. $x^2=-9$인 $x$가 존재할까? 이 질문은 매우 바보 같아 보일 수도 있다. 충분히 바보 같은 질문이다. 이 문제에 대한 해답은 $x^2=-1$인 $x$가 존재 한다고 수의 개념을 확장시키면 찾을 수 있을 것이다. 그럼 소위 라고 불리는 imaginary number가 지금까지 얘기했던 수 체계가 1차원 벡터로 확장되었다는 것과는 어떤 관계가 있는 것일까?

허수의 발견은 지금까지 실수 영역에서 1차원 벡터로 표현 될 수 있었던 수 체계를 2차원 벡터로 확장시켰다는 놀라운 의미를 갖는다.¹ 왜 그런지 곱셈 연산이 방향성을 가지는 연산이라는 사실을 바탕으로 생각해보자. 허수의 개념을 정확하게 이해하려면 제곱이 갖는 의미에 대해서 다시 한 번 생각해보아야 할 것이다. 제곱이란 무엇인가? 같은 수를 두 번 곱해준다는 의미이다. 즉, $x^2$는 $1\times x\times x$의 의미를 갖는다. 그러니까, $3^2$는 다음과 같은 의미를 갖는다. $1\times 3\times 3$. 즉, 1이라는 원래의 수를 양의 방향으로 3배 만큼 커지게 하고, 또 양의 방향으로 3배 만큼 커지게 한다는 의미이다.

이번엔 음수의 제곱을 생각해보자. $(-3)^2$은 어떤가? 이것은 $1\times (-1) \times 3 \times (-1) \times 3$의 의미를 갖게 될 것이다. 이것은 1이라는 숫자를 음의 방향에서 3배 만큼 커지게 하고, 다시 한 번 그 반대 방향에서 3배 만큼 커지게 할 것이라는 의미를 갖는다. 이것은 이제 역으로 생각해서 $x^2=9$일 때, $x=3$ 또는 $x=-3$이라는 사실을 생각해 낼 수 있게 되는 것이다. 그러니까 $1\times 3\times 3$을 생각해 볼 때 이 수식은 ‘1을 양의 방향으로 3배 커지게 하고, 또 한 번 더 양의 방향으로 3배 커지게 했을 때 9가 될 수 있다.’ 라고 해답을 찾을 수도 있고, 또는 ‘1을 음의 방향에서 3배 커지게 하고, 한 번 더 음의 방향에서 3배 커지게 하면 9가 될 수 있다’는 의미를 갖고 있다.

그렇기 때문에 음의 방향이라는 것은 상대적으로 반대방향을 의미하는 것이라는 것도 알 수 있다. 이제 다시 한 번 $x^2=-9$가 갖는 의미에 대해서 생각해보자. $x^2=-9$라는 말은 $1\times x\times x=-9$이므로 같은 수를 이용해 두 번 곱셈 연산이라는 변환을 취해줬을 때 –9가 나올 수 있어야 한다. 이제 우리는 실수 $x$를 가지고는 이 방정식을 풀 수 없다는 사실을 알 수 있다. 왜냐면, 양수를 두 번 곱하면 양수가 되고, 음수를 두 번 곱하면 다시 양수가 되기 때문이다. **그래서 허수는 ‘회전’이라는 개념을 도입한 수가 되는 것이다. ** 수의 회전이라고 하면 언뜻 듣기엔 말이 되지 않는 것 같지만 아래의 그림을 살펴보자.

실수라는 축에 국한 되어 있지 않고 수 체계의 추가적인 차원의 축이 있다고 한다면, 방향성을 가지는 1차원의 벡터가 +90도 회전하고, 한번 더 +90도 회전한다면, 그 결과는 –1이 될 수 있는 것이다. 그러니까 곱셈 연산이 방향성을 가질 수 있다고 한 것이 1차원 선상의 앞, 뒤 만 의미할 필요는 없지 않느냐는 것이다. 즉, 실수까지의 수 체계를 하나의 축 위에 표현할 수 있는 것처럼, 허수라는 수는 실수 차원의 축과 직교하는 새로운 하나의 축을 담당할 수 있는 것이다.

그렇기 때문에 새로운 차원의 수인 허수의 개념의 발견은 수가 1차원이 아니라는 사실을 알 수 있게 한다. 즉, 허수 $i$가 imaginary dimension으로의 90도 CCW 회전을 의미한다면 1차원인 실수 영역에서 보았을 때는 $i^2=-1$인 것이다.² 1차원에서만 생각한다면 매우 기이한 현상처럼 보일 것이다. 3차원에 사는 우리가 4차원에서 일어나는 세계를 이해할 수 없는 것처럼 말이다.