※ Wold’s theorem은 위너-킨친 정리의 Discrete Time Random Signal 버전이라고 할 수 있다.

1. Discrete Time Random Signal의 Power Spectrum Density (PSD)

※ 해당 내용은 Richard Shiavi의 Introduction to applied statistical signal analysis, 3e.pp.203 - 205 의 내용을 옮겨 적은 것임.

Wide-sense stationary random signal의 푸리에 변환을 생각할 때의 가장 큰 문제점은 푸리에 변환이 존재하지 않는다는 것이다. 다시 말해 $X(f)$가 존재하기 위해서는 신호의 에너지가 유한해야 한다. 다시 말해 아래와 같은 식을 만족해야 한다는 뜻이다.

\[energy = T\sum_{n=-\infty}^{\infty}x(n)^2 \lt \infty\]

$x(n)$은 최소한 wide-sense stationary 하므로 모든 sample function의 energy는 양의 무한대로 발산하게 된다(Priestly, 1981)¹. 실제로 평균 에너지 역시 양의 무한대로 발산하게 된다.

\[E\lbrace energy\rbrace = T\sum_{n=-\infty}^{\infty}E \lbrace x(n)^2\rbrace = \infty\]

그런데, 평균 energy 대신에 평균 power는 유한한 양이므로 frequency transformation의 정의에 기반이 될 값으로 사용될 수 있을 것이다. 평균 파워는 다음과 같이 정의된다.

\[E\lbrace power\rbrace = \lim_{N\rightarrow \infty}\sum_{n=-N}^{N}\frac{T E\lbrace x(n)^2\rbrace}{(2N+1)T} = E\lbrace x(n)^2\rbrace \lt \infty\]

여기서, 주파수 변수를 위 식에 포함 시키기 위해 아래와 같이 $x_p(n)$을 정의하자.

\[x_p(n) = \begin{cases}x(n) && |n|\leq N \\ 0 && |n| \gt N \end{cases}\]

여기서 Parseval’s theorem에 따라 다음이 성립한다.

\[T\sum_{n=-\infty}^{\infty}x_p(n)^2 = \int_{-1/2T}^{1/2T}X_p(f)X^*_p(f) df\]

$x_p(n)$의 sequence는 유한하기 때문에 위의 summation limits 는 $-N$에서 $N$까지로 변경될 수 있다. 따라서 다음이 성립한다.

\[E\lbrace power\rbrace = \lim_{N\rightarrow \infty}E\left\lbrace \sum_{n=-N}^{N}\frac{T x_p(n)^2}{(2N+1)T}\right\rbrace\] \[= \lim_{N\rightarrow \infty}E\left\lbrace \frac{\int_{-1/2T}^{1/2T}X_p(f)X^*_p(f) df}{(2N+1)T}\right\rbrace\] \[=\int_{-1/2T}^{1/2T}\lim_{N\rightarrow \infty}E\left\lbrace \frac{X_p(f)X^*_p(f)}{(2N+1)T}\right\rbrace df\]

여기서 피적분함수를 power spectral density (PSD)라고 한다.

\[S(f) = \lim_{N\rightarrow \infty} E\left\lbrace \frac{X_p(f) X^*_p(f)}{(2N+1)T}\right\rbrace\]

2. Wold’s Theorem의 증명

Wold’s theorem의 결과는 다음과 같다.

\[S(f) = T\sum_{k=-\infty}^{\infty}R(k) \exp(-j2\pi fkT)\]

위의 식 (9)와 같은 $S(f)$의 정의를 이용해 이를 증명해보도록 하자.

식 (9)에서 극한 내의 값에 대해 조금 더 자세히 살펴보도록 하자.

DTFT의 정의에 의해 다음이 성립한다.

\[E\left\lbrace \frac{X_p(f)X^*_p(f)}{(2N+1)T}\right\rbrace = E\left\lbrace \frac{1}{(2N+1)T}\left(T\sum_{n=-N}^{N}x(n)\exp(-j 2\pi fnT)\right)\left(T\sum_{l=-N}^{N}x(l)\exp(-j 2\pi flT)\right)^*\right\rbrace\]

여기서 선형 연산자를 정리하면 다음과 같다.

\[\Rightarrow \frac{T^2}{(2N+1)T}\sum_{n=-N}^{N}\sum_{l=-N}^{N} E\lbrace x(n)x(l)\rbrace \exp(-j2\pi f(n-l) T)\]

Discrete time signal $x(n)$이 wide-sense stationary 하다고 가정한다면 다음이 성립한다.

\[\Rightarrow \frac{T}{(2N+1)}\sum_{n=-N}^{N}\sum_{l=-N}^{N}R(n-l)\exp(-j2\pi f(n-l) T)\]

여기서 $R(\cdot)$은 autocorrelation function이다.

이제

\[\sum_{n=-N}^{N}\sum_{l=-N}^{N}R(n-l)\exp(-j2\pi f(n-l) T)\]

을 계산하는 방법에 대해 다음과 같이 생각해보도록 하자. $n$과 $l$을 독립변수라고 생각해보자. 이 때, $n$과 $l$은 다음과 같은 범위를 갖는다.

\[-N\leq n \leq N\] \[-N \leq l \leq N\]

또한, $n$과 $l$은 discrete 변수이고 interval은 1이다.

따라서, 아래의 그림처럼 식 (14)를 생각할 수 있다. 이 때, 각각의 점들은 $n$과 $l$의 값이 얼망리 때 대응되는 $R(n-l) \exp(-j2\pi f(n-l)T)$의 값이다.

즉, 아래 그림에서 검은 동그라미를 모두 그리지는 않았지만 $-N\leq n \leq N$, $-N \leq n \leq N$의 내부에 검은 동그라미가 모두 꽉 찬 상태가 될 것이다.

그리고 각 검은 동그라미에 해당되는 $R(n-l) \exp(-j2\pi f(n-l)T)$의 값을 모두 더한 것이 식 (14)를 구한 것과 같은 결과를 얻을 수 있게 되는 것이다.

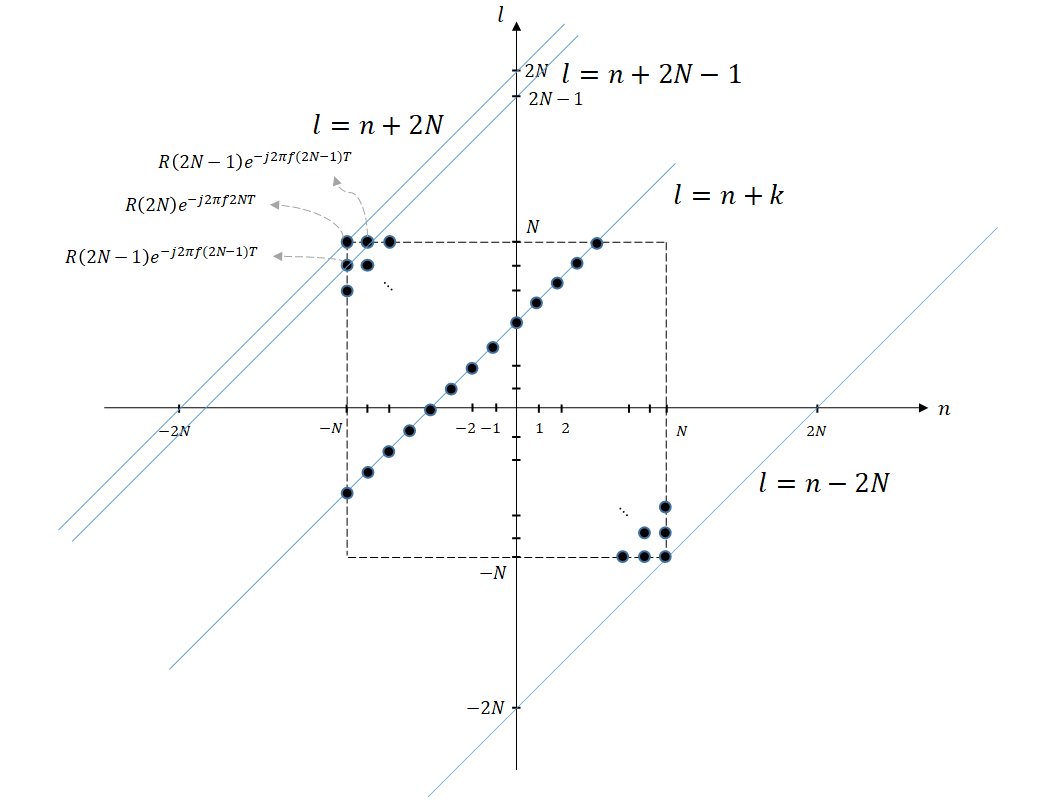
그림 1.

이 때, $k=n-l$이라고 하면 $l=n-k$가 되는 것이고 이것은 기울기가 1인 1차 함수가 된다. 그림에 따르면 $k$의 범위는 $-2N \lt k \lt 2N$이라는 것을 알 수 있다.

그리고 $k$의 값이 $-2N$에서 $2N$으로 변하는 동안 더해야 할 $R(n-l)\exp(-j2\pi f(n-l)T)$의 값을 확인해보면 다음과 같다.

\[k=2N \Rightarrow R(2N)\exp(-j2\pi f (2N) T)\] \[k=2N-1 \Rightarrow 2\times R(2N-1)\exp(-j2\pi f (2N-1) T)\] \[k=2N-2 \Rightarrow 3\times R(2N-2)\exp(-j2\pi f (2N-2) T)\] \[\vdots\notag\] \[k=0 \Rightarrow (2N+1)\times R(0)\exp(-j2\pi f (0) T)\] \[\vdots\notag\] \[k=-(2N-2) \Rightarrow 3\times R(2N-2)\exp(-j2\pi f (2N-2) T)\] \[k=-(2N-1) \Rightarrow 2\times R(2N-1)\exp(-j2\pi f (2N-1) T)\] \[k=-2N \Rightarrow R(2N)\exp(-j2\pi f (2N) T)\]

따라서 모든 $k$에 대하여 $k=n-l$일 때 식 (14)의 값은 아래와 같이 표현할 수 있게 된다.

\[\sum_{k=-2N}^{2N}(2N+1-|k|)R(k)\exp(-j2\pi fkT)\]

그러므로, 우리가 구하고자 하는 식 (13)은

\[식(13)\Rightarrow \frac{T}{(2N+1)}\sum_{k=-2N}^{2N}(2N+1-|k|)R(k)\exp(-j2\pi fkT)\] \[=T\sum_{k=-2N}^{2N}\left(1-\frac{|k|}{2N+1}\right)R(k)\exp(-j2\pi fkT)\]

이 된다.

따라서,

\[S(f) = \lim_{N\rightarrow \infty}\sum_{k=-2N}^{2N}T\left(1-\frac{|k|}{2N+1}\right)R(k)\exp(-j2\pi fkT)\] \[=T\sum_{k=-\infty}^{\infty}R(k)\exp(-j2\pi fkT)\]

가 된다.

또한, DTFT의 정의에 따라

\[R(k) =\int_{-1/2T}^{1/2T}S(f)\exp(j2\pi fkT)df\]

이다.