What the determinant represents: How much does the unit area change when linearly transformed?

※ In this article, we follow the column vector convention.

Determinant

The determinant is used to find the inverse of a matrix. For a $2\times 2$ matrix, the determinant is defined as follows:

DEFINITION 1. Determinant
Let $$A=\begin{pmatrix}a& b \\ c & d \end{pmatrix}$$ Then $$det(A) = ad-bc$$ is defined as the determinant of A.

The inverse of a $2\times 2$ matrix is defined as follows:

DEFINITION 2. Inverse of a 2 x 2 matrix
Let $$A=\begin{pmatrix} a& b \\ c & d \end{pmatrix} \notag$$ Then $$A^{-1} = \frac{1}{det(A)} \begin{pmatrix}d& -b \\ -c & a \end{pmatrix}$$ is defined as the inverse of A.

While it is possible to show algebraically that $AA^{-1} = A^{-1}A = I$, the determinant appears in many mathematical fields that use matrices beyond linear algebra. In particular, in geometry, the determinant plays a vital role. But what does the determinant of a matrix mean geometrically? the determinant of a $2 \times 2$ matrix represents the area of the parallelogram formed by the two transformed basis vectors after a linear transformation, as explained in the article “Matrix and Linear Transformation.” An arbitrary matrix

\[A=\begin{pmatrix} a& b \\ c & d \end{pmatrix}\notag\]

performs the role of transforming the basis vectors $\hat{i} = (1,0)$ and $\hat{j} = (0,1)$ into new basis vectors $\hat{u} = (a,c)$ and $\hat{v} = (b,d)$, as mentioned in the article¹.

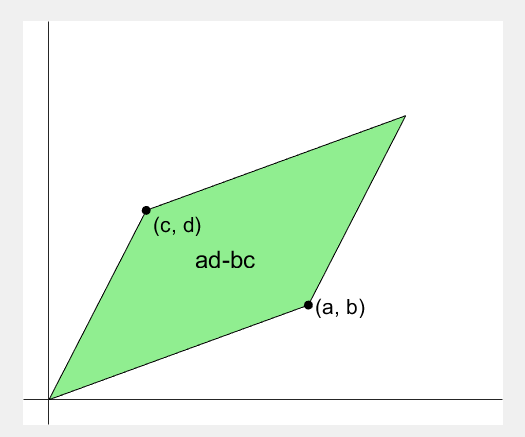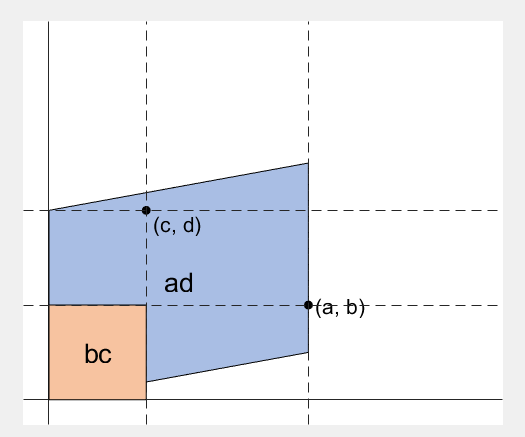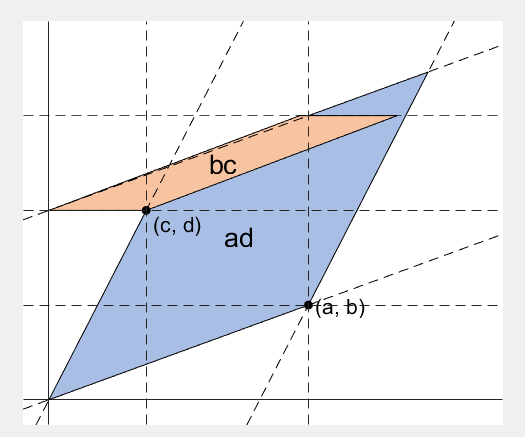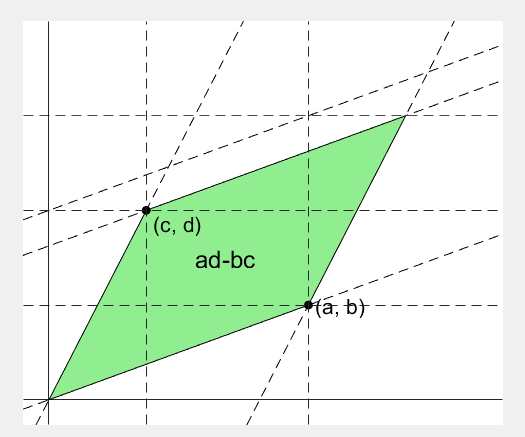
Arbitrary basis vectors $\vec{u}$ and $\vec{v}$ can be represented graphically on the coordinate plane, as shown in Figure 1.

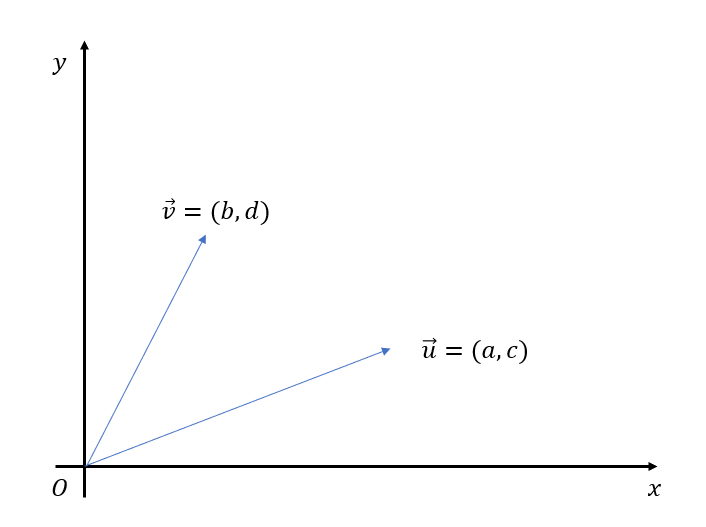
In this case, as explained in Figure 2, the area of the parallelogram AVOU formed by the two vectors represents the determinant $det(A)$. The area of the parallelogram AVOU is twice the area of the triangle VOU. Therefore, by finding the area of the triangle VOU and multiplying it by two, we can determine the area of the parallelogram AVOU.

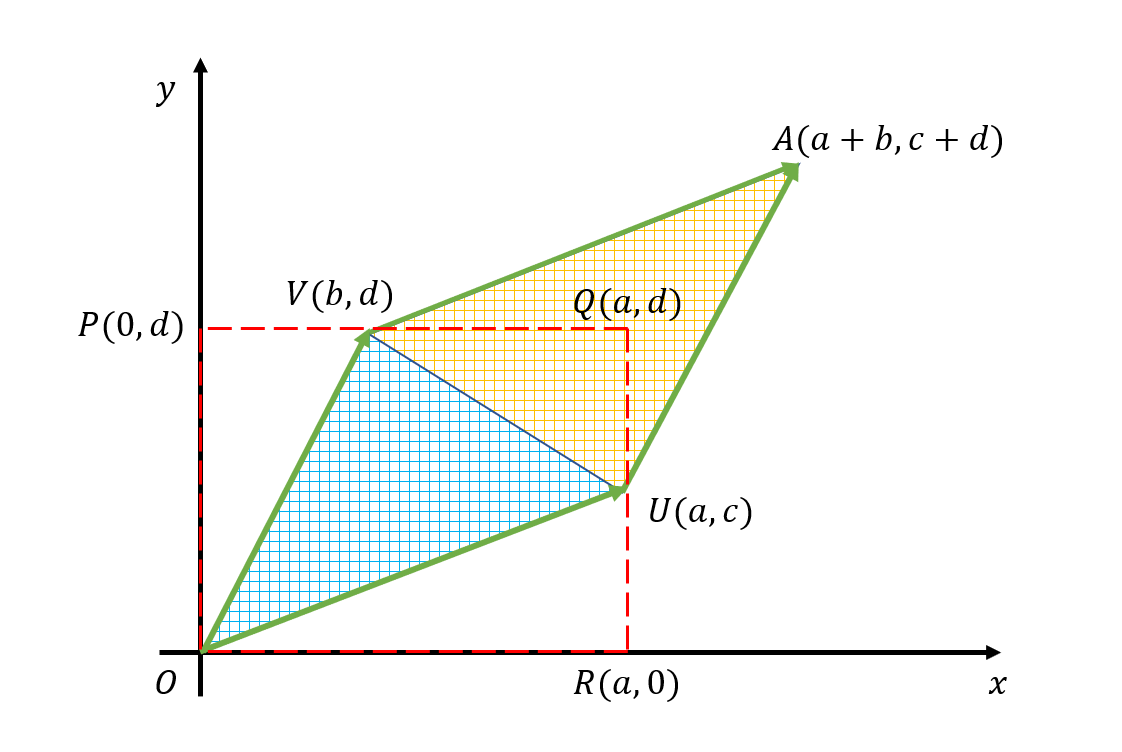
The area of the triangle VOU is equal to the area of the shaded part in the dashed rectangle PORQ minus the areas of the triangles POV, UOR, and VUQ. Hence, the area of the parallelogram AVOU can be found by calculating the area of the triangle VOU and multiplying it by two.

\[◇AVOU = \notag\] \[=2\times\left\{□PORQ - △POV - △UOR - △VUQ\right\}\] \[=2\times \left\{ad-\frac{1}{2}bd -\frac{1}{2}ac - \frac{1}{2}(a-b)(d-c)\right\}\] \[=2\times\left\{ ad-\frac{1}{2}bd-\frac{1}{2}ac-\frac{1}{2}(ad-bd-ac+bc) \right\}\] \[=2\times\left\{ ad-\frac{1}{2}bd-\frac{1}{2}ac-\frac{1}{2}ad+\frac{1}{2}bd+\frac{1}{2}ac-\frac{1}{2}bc) \right\}\] \[=2\times\left\{ \left(ad-\frac{1}{2}ad\right) +\left(\frac{1}{2}bd-\frac{1}{2}bd\right) +\left(-\frac{1}{2}ac+\frac{1}{2}ac\right) -\frac{1}{2}bc) \right\}\] \[=2\times\left\{\frac{1}{2}ad-\frac{1}{2}bc\right\}\] \[=ad-bc = det(A)\]

The Geometric Relationship between Matrices, Inverse Matrices, and Determinants

In the previous discussion, matrices were defined geometrically as linear transformations.

In this sense, the inverse matrix can also be treated as another matrix that is associated with the original matrix and represents the reverse linear transformation.

Geometrically, the inverse matrix can be considered as the reverse-linear transformation using the original matrix. In other words, the linear transformation through the matrix described in the previous explanation changes a unit square with side length 1 into a parallelogram with an area of ad-bc. The inverse matrix of the same matrix is the inverse-reverse transformation that changes the parallelogram back into a unit square with side length 1.

Therefore, the inverse matrix includes the element of $1/det(A)$.

Finally, I would like to attach a very useful animation that visually demonstrates the value “ad-bc” in the determinant.

Why is determinant equal to "ad-bc"?
Original Source: Lazy MATLAB( https://lazymatlab.tistory.com/201/)