This post is a summary of Professor S.C. Duta Roy’s lecture at IIT, which can be found at this link.
Objectives
- Understand the characteristics of Chebyshev filters compared to Butterworth filter.
- Understand the characteristics of Chebyshev polynomials.
- Understand the determination methods for the implementation conditions of Chebyshev filters, namely the value of $N$ and $\epsilon$.
1. Characteristics of Chebyshev filters
a. Introduction to Chebyshev Filter
Like the Butterworth filter, the Chebyshev filter is an all-pole filter that is primarily designed for low-pass filter design.
As described in the previous post about the Butterworth filter, this post will also focus on the design of low-pass filters using Chebyshev filters.
In general, the Chebyshev filter can be considered the closest to an ideal filter when compared to other types of filters, excluding elliptic filters. This is because for the same filter order ($N$) and specification requirements, the transition band is the narrowest and the transition slope is the steepest.
Note that elliptic filters can only be created using numerical methods. Therefore, excluding elliptic filters, the Chebyshev filter is the most optimal type of filter that can be determined through mathematical equations.
b. Shape of Chebyshev Filters
So let’s take a look at the rough shape of the Chebyshev filter.
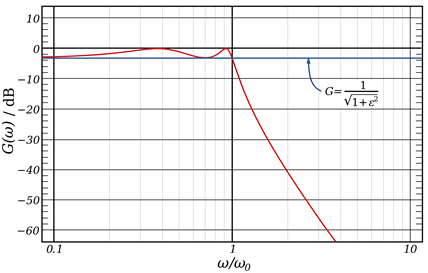
Figure 1. Rough form of Chebyshev filter
Source: Wikipedia Chevyshev filter
The most notable characteristic visible from its appearance is the ripple within the passband.
To list some of the characteristics of the Chebyshev filter in more detail:
① It is not a monotonic filter.
② It has equal ripple (Equi-Ripple).
In Type I Chebyshev filters, there is ripple within the passband, but the stopband shows a monotonic trend. In contrast, Type II shows the opposite trend, and Type II can be obtained by reversing Type I. However, Type I is preferred because Type II is vulnerable to unnecessary signal removal in the role of a lowpass filter.
As for the reason for ②, it will be explained in more detail later, but there is a difference between the ripple shape in the figure and the actual periodic ripple that exists, and there is also a formula for the ripple. The equation that determines the shape and period of the ripple is called the Chebyshev Polynomial and is denoted by $C_N(x)$.
c. What can we learn from the equations?
The Chebyshev filter is defined by the following equation:
\[|H_a(j\Omega)|^2 = A^2 / \left\lbrace 1+\epsilon^2 C_N\left(\frac{\Omega}{\Omega_p}\right)\right\rbrace\]or
\[|H_a(j\Omega)| = A / \sqrt{ 1+\epsilon^2 C_N\left(\frac{\Omega}{\Omega_p}\right)}\]Here, A is the gain factor. Typically, if you don’t want amplification at the passband frequency, set A to 1.
If we take a closer look at this equation, we can see the characteristics of the Chebyshev filter. When compared specifically to the Butterworth filter, it can help us to gain a more intuitive understanding. The equation for the Butterworth filter is as follows:
\[|H_a(j\Omega)|^2 = 1/\left\lbrace 1+\left(\frac{\Omega}{\Omega_c}\right)\right\rbrace\]In other words, the equation for the Chebyshev filter contains elements that are not present in the equation for the Butterworth filter, namely $\epsilon$ and $C_N(x)$. A minor but important difference between the Chebyshev and Butterworth filter is that the Chebyshev filter equation includes $\Omega_p$, while the Butterworth filter includes $\Omega_c$. This means that when implementing the Chebyshev filter, we do not directly need $\Omega_c$.
$\epsilon$ determines the size of the ripple, while $C_N(x)$ determines the shape of the ripple based on the order N of the filter. $C_N(x)$ is defined as follows:
\[C_N(x) = \begin{cases}\cos(N\cos^{-1}(x)) && \text{ for } |x| \leq 1 \\\cosh(N\cosh^{-1}(x)) && \text{ for } |x| \gt 1\end{cases}\]If we examine this equation closely, we can see why the range of $x$ is defined around 1. This is because the function $cos^{-1}(x)$ is defined for $|x|\leq 1$, and the values of $C_N(x)$ are different when $\Omega$ is greater than or less than $\Omega_p$. In other words,
① $cos(N\cos^{-1}(x))$ is a cosine function, which means that it will have ripple, and this ripple will have a period of $N\cos^{-1}(x)/{2\pi}$.
② $\cosh(N\cosh^{-1}(x))$ is not a periodic function. The $\cosh(x)$ function is called the hyperbolic cosine and is defined as follows:
\[\cosh(x) = \frac{e^x+e^{-x}}{2} = \cos(jx)\]Therefore, from the equation, we can see that when $\Omega\leq\Omega_p$, the function has periodic ripple, and when $\Omega>\Omega_p$, it is a monotonic function.
2. Chebyshev polynomial $(C_N(x))$
a. Definition of Chebyshev polynomial
Once again, the definition of Chebyshev Polynomial is as follows:
\[C_N(x) = \begin{cases}\cos(N\cos^{-1}(x)) && \text{ for } |x| \leq 1 \\\cosh(N\cosh^{-1}(x)) && \text{ for } |x| \gt 1\end{cases}\]We want to emphasize that we are interested in $C_N(x)$ when $|x|\leq 1$. This is important because the properties of $C_N(x)$ determine the shape of the Chebyshev filter.
b. Analyzing Chebyshev polynomial
First, let’s revisit the interpretation of $C_N(x)=\cos(N\cos^{-1}(x))$. We want to analyze the shape of $C_N(x)$ as $N$ varies. This is because the main determining factors of the Chebyshev filter are the filter order $N$ and the ripple size factor $\epsilon$.
\[C_0(x) = 1\] \[C_1(x) = \cos(1\times \cos^{-1}(x)) = x\]To find $C_2(x)$, we need to use a little bit of algebra.
\[C_2(x) = \cos(2\cos^{-1}(x))\]Let’s call $\cos^{-1}(x)=\theta$. Then $x=\cos(\theta)$. Therefore,
\[C_2(x) = \cos(2\theta) = 2\cos^2\theta - 1 = 2x^2 - 1\]We can also find $C_3(x)$ using a similar method.
\[C_3(x) = \cos(3\cos^{-1}(x))\]Similarly, let’s call $\cos^{-1}(x)=\theta$. Then $x=\cos(\theta)$. Therefore,
\[C_3(x) = \cos(3\theta) = \cos(2\theta + \theta)\]Here,
\[\cos(2\theta + \theta)=\cos(2\theta)\cos(\theta) - \sin(2\theta)\sin(\theta)\] \[=(2\cos^2(\theta)-1)\cos(\theta) - 2\sin(\theta)\cos(\theta)\sin(\theta)\] \[=(2\cos^3(\theta) - \cos(\theta))-2(1-\cos^2(\theta))\cos(\theta)\] \[=2\cos^3(\theta) - \cos(\theta) - 2\cos(\theta) + 2\cos^2(\theta)\] \[=4\cos^3(\theta)-3\cos(\theta)\]Therefore, the original $C_3(x)$ is
\[\Rightarrow C_3(x) = 4x^3-3x\]When we observe the shape of $C_N(x)$, we can see that the degree of $x$ differs by 2.
Therefore, by using the following general formula,
\[\cos(x) + \cos(y) = 2\cos\left(\frac{x+y}{2}\right)\cos\left(\frac{x-y}{2}\right)\]we can obtain
\[\cos(N\theta) + \cos((N-2)\theta) = 2\cos(\theta)\cos((N-1)\theta)\]and, using the equation
\[\cos^{-1}(x) = \theta, x = \cos(\theta)\]we can obtain
\[C_N(x) = \cos(N\cos^{-1}(x))\]and
\[C_N(x) = \cos(N\theta)\]Therefore, we can derive the fact that
\[C_N(x) = 2xC_{N-1}(x) - C_{N-2}(x)\]and we can derive the general formula for $C_N(x)$.
Hence, For example,
\[C_3(x) = 2x(2x^2 -1) -x\] \[= 4x^3 - 3x\] \[C_4(x) = 2xC_3(x) - C_2(x)\] \[=2x(4x^3-3x) - (2x^2 - 1)\] \[=8x^4 - 8x^2 + 1\]In the same way, we can recursively calculate the value of any $C_N(x)$ regardless of the size of N.
Let’s take a look at some $C_N(x)$.
\[C_0(x) = 1\] \[C_1(x) = x\] \[C_2(x) = 2x^2 - 1\] \[C_3(x) = 4x^3 - 3x\] \[C_4(x) = 8x^4-8x^2 + 1\]If we gather $C_N(x)$ like this, we can see that $C_N(0)$ has a peculiar periodicity.
It is:
\[C_N(0) = \begin{cases}0 && N = \text{odd}\\\pm 1 && N = \text{even}\end{cases}\]This plays an important role in determining the shape of the Chebyshev filter at $\Omega=0$.
Also, if we gather the Chebyshev Polynomials $C_N(x)$, we get:
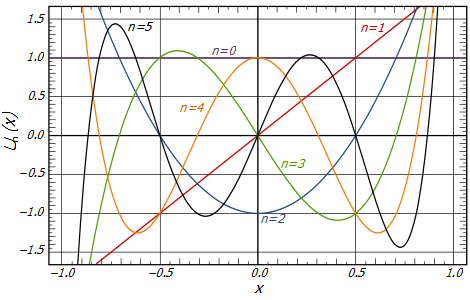
Figure 2. Chebyshev Polynomials for various n
Source: Wikipedia, Chevyshev filter
For $|x|>1$, we can draw a continuous line along the respective color. This is because $C_N(x)$ is defined as $C_N(x)=\cosh(\cosh^{-1}(x))$ for $|x|>1$, and as mentioned before, it has a monotonic shape.
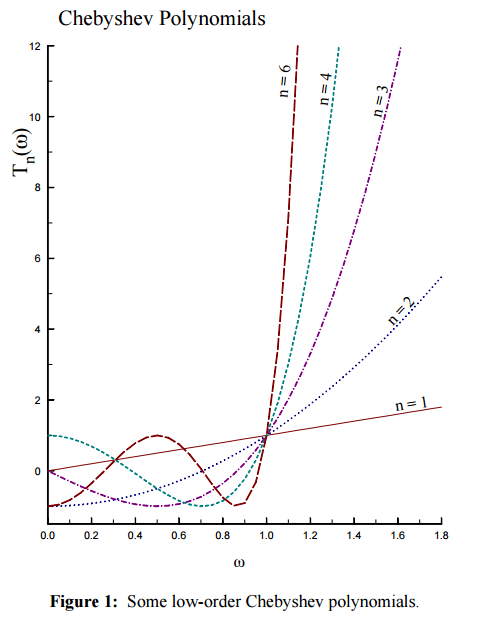
Figure 3. The Chebyshev Polynomials extended and plotted for various values of n for $\|x\|>1$
(Source: EE648 Chebyshev filters / John Stensby / ece.uah.edu)
Therefore, we can see that the ripple shown in the Chebyshev filter oscillates equally.
c. The Shape of Chebyshev Filter Depending on N
Let’s write the formula for the Chebyshev filter again:
\[|H_a(j\Omega)| = A / \sqrt{ 1+\epsilon^2 C_N\left(\frac{\Omega}{\Omega_p}\right)}\]Here, let’s think about the maximum and minimum values of $|H_a(j\Omega)|$ to draw the shape of the Chebyshev filter.
$C_N$ oscillates for $0\leq\Omega\leq\Omega_p$ and its value satisfies $0\leq C^2_N\leq 1$.
\[\frac{A}{\sqrt{1+\epsilon^2}}\leq|H_a(j\Omega)|\leq A\]If we assume that $A=1$ here,
\[\frac{1}{\sqrt{1+\epsilon^2}}\leq|H_a(j\Omega)|\leq 1\]Therefore, for each degree N of the filter, we can see its shape as follows:
When $N=1$,
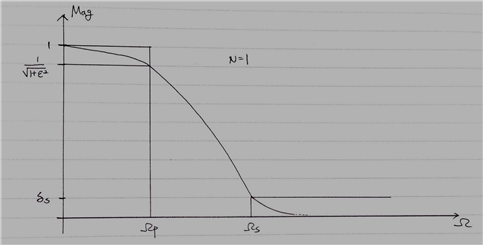
Figure 4. The shape of Chebyshev filter for $N=1$
Since $N$ is odd, $C_1(0)=0$. Also, $|H_a(j\Omega)|_{\Omega = 0}=1$.
Therefore, we can see that when N=1, the Chebyshev filter starts at 1. Moreover, when N=1, it has a similar appearance to a Butterworth filter. However, depending on the value of $\epsilon$, it may or may not have the same values as a Butterworth filter, so having a similar shape does not necessarily mean that it is the same filter.
When N=2,
\[C_2(0)=2\times0^2-1=-1\]and,
\[C_2(\Omega_p)=1\]Therefore,
\[|H_a(0)|=\frac{1}{\sqrt{1+\epsilon^2}}\]If we draw the shape of the filter, we get the following:
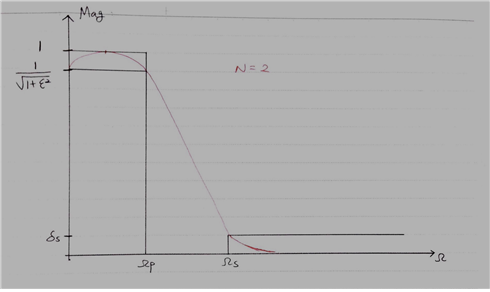
Figure 5. Shape of the Chebyshev filter when N=2.
We can also draw the Chebyshev filter for N=3 and N=4, respectively.
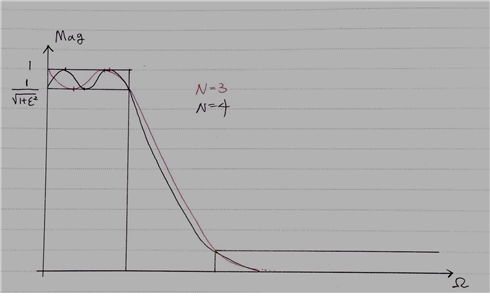
Figure 6. Shape of the Chebyshev filter when N=3 and N=4, respectively.
When we look at this point, all Chebyshev filters have one thing in common, which is that all Chebyshev filters pass through the point
\[\left(\Omega_p, \frac{1}{\sqrt{1+\epsilon^2}}\right)\]regardless of the size of $N$.
This can be explained by the fact that all Chebyshev Polynomials pass through $(1,1)$, or that $C_N(x)=\cos(N\cos^{-1}(x))$ and $C_N(x)=\cos(N\cos^{-1}(x))=\cos(N\times 2\pi)=1$ can be directly proven. We will be able to calculate the size of $N$ later using this fact.
To summarize a few facts,
① The number of Maxima & Minima within the Passband = N
② If $N$ = even, starting point = $1/\sqrt{1+\epsilon^2}$
else if $N$ = odd, starting point = $1$
One more thing to consider here is how to find the 3dB frequency (or cutoff frequency). Using the definition of 3dB, it can be expressed as:
\[|H_a(j\Omega)|^2 = \frac{1}{2}\]Therefore,
\[1/\left\lbrace1+\epsilon^2C_N\left(\frac{\Omega_{3dB}}{\Omega_p}\right)\right\rbrace=\frac{1}{2}\] \[\therefore \epsilon^2 C^2_N\left(\frac{\Omega_{3dB}}{\Omega_p}\right)= 1\] \[C_N\left(\frac{\Omega_{3dB}}{\Omega_p}\right)=\frac{1}{\epsilon}\]Typically, $\epsilon$ is defined as a “small value,” and because of the characteristics of the Chebyshev filter, $\epsilon$ must be less than 1. Therefore, if we use $C_N(x)=\cosh(N\cosh^{-1}(x))$, we can obtain:
\[\cosh\left(N\cosh^{-1}\left(\frac{\Omega_{3dB}}{\Omega_p}\right)\right)=\frac{1}{\epsilon}\] \[\therefore \Omega_{3dB}=\Omega_p\left\lbrace\cosh\left(\frac{1}{N}\cosh^{-1}(1/\epsilon)\right)\right\rbrace\]3. General transfer function of Chebyshev filter in s-domain
a. Finding poles of Chebyshev filter
According to the definition of a pole, a pole can be said to be a value of s that satisfies the following equation:
\[1+\epsilon^2C^2_N\left(\frac{s}{j\Omega_p}\right) = 0\]However, unfortunately, I couldn’t fully understand the algebra needed to solve this equation. Therefore, I will omit the explanation of the algebra to find poles.
However, the conclusion is that when we find the poles, they will be located on an ellipse, unlike the poles of the Butterworth filter. For a detailed explanation, please refer to Wikipedia.
b. The transfer function of Chebyshev filter
Like the Butterworth filter, the Chebyshev filter can also be divided into two cases when the degree of N is even and odd. As seen in the overall shape of the Chebyshev filter according to the degree of N described above, the starting point differs depending on whether N is even or odd, and therefore the formula also changes accordingly.
$N$ : odd
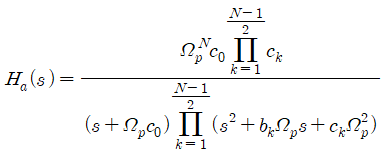
$N$ : even
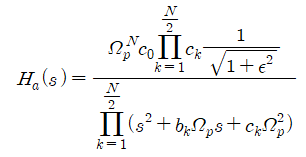
As can be seen from the above equations, when N is even, the starting point is $1/\sqrt{1+\epsilon^2}$, which is multiplied in the numerator. Regarding each constant $c_0$, $b_k$, and $c_k$, we can say that:
\[c_0 = y_N\] \[c_k = y^2_N+\cos^2\left(\frac{2k-1}{2N}\pi\right)\] \[b_k = 2y_N\sin\left(\frac{2k-1}{2N} \pi\right)\] \[y_N = \frac{1}{2}\left\lbrace \left(\sqrt{1+\frac{1}{\epsilon^2}}+\frac{1}{\epsilon}\right)^{\frac{1}{N}} - \left(\sqrt{1+\frac{1}{\epsilon^2}}+\frac{1}{\epsilon}\right)^{-\frac{1}{N}}\right\rbrace\]Finally, we need to consider how to determine N and $\epsilon$.
c. How to determine $N$ and $\epsilon$
When designing a filter, one must be aware of the specifications received, which are $\Omega_p, \Omega_s, \delta_p,$ and $\delta_s$. These are the requirements that the filter should meet. They are not mathematically determined but are set by the designer or the customer.
Generally, the relationship between specifications can be expressed as follows:
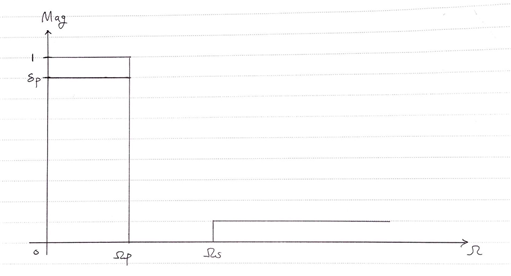
Figure 7. Specifications given when designing a filter
As explained earlier, since $\delta_p$ is a given value,
\[\delta_p = \frac{1}{\sqrt{1+\epsilon^2}}\] \[\therefore \epsilon = \sqrt{\frac{1}{\delta^2_p-1}}\]The value of $N$ can be determined as follows:
Using the fact that $\delta_s$ is also a given value,
\[1/\left\lbrace1+\epsilon^2 C_N\left(\frac{\Omega_s}{\Omega_p}\right)\right\rbrace=\delta_s^2\] \[\therefore\epsilon^2 C^2_N\left(\frac{\Omega_s}{\Omega_p}\right)=\frac{1}{\delta_s}-1\] \[C_N\left(\frac{\Omega_s}{\Omega_p}\right)=\sqrt{\frac{1/\delta_s^2-1}{1/\delta^2_p - 1}}\]Here,
\[\left(\frac{\Omega_s}{\Omega_p}\right)\gt 1\]so,
\[C_N\left(\frac{\Omega_s}{\Omega_p}\right)=\cosh\left(N\cosh^{-1}\left(\frac{\Omega_s}{\Omega_p}\right)\right) = \sqrt{\frac{1/\delta_s^2-1}{1/\delta^2_p - 1}}\] \[N_C\geq\frac{\cosh^{-1}\left(\sqrt{\frac{1/\delta_s^2-1}{1/\delta^2_p - 1}}\right)}{\cosh^{-1}\left(\frac{\Omega_s}{\Omega_p}\right)}\]we can find $N_C$ that satisfies the above equation. (Here, $C$ in $N_C$ stands for Chebyshev.)
For reference, the order $N_B$ of the Butterworth filter was as follows:
\[N_B\geq \frac{\log_{10}\sqrt{\frac{1/\delta^2_s-1}{1/\delta^2_p-1}}}{\log_{10}\left(\frac{\Omega_s}{\Omega_p}\right)}\]In the end, we can say that the methods for determining $N$ in Chebyshev and Butterworth filter are very similar.