Formula of Bayes’ Theorem

Let’s first take a look at the formula of Bayes’ theorem. The formula of Bayes’ theorem is as follows:

\[P(H|E) = \frac{P(E|H)P(H)}{P(E)}\]

Formula (1) contains four probability values, and its appearance is almost identical, making it difficult to understand its meaning at a glance.

Among the four probability values, $P(H)$ and $P(H|E)$ are respectively called the prior probability and posterior probability, and Bayes’ theorem fundamentally represents the relationship between the prior and posterior probabilities.

Therefore, by understanding the meanings of prior and posterior probabilities, we can understand what Bayes’ theorem is saying and its significance.

Meaning and Significance of Bayes’ Theorem

In summary, Bayes’ theorem is a method to update belief on the basis of new information.

Reasons why Bayes’ Theorem is difficult to understand

The first concept that needs to be clarified in understanding Bayes’ theorem is the perspective on “probability.”

One of the reasons why it is difficult to understand the meaning of Bayes’ theorem is that until high school level, probability has been defined and understood from a “traditional perspective” in probability theory.

Let’s think of the word “probability” as “confidence in a claim.”

This perspective can be seen as the Bayesian view of probability. On the other hand, the traditional view of probability can be seen as frequentism.

For example, if we say that the probability of getting heads when flipping a coin is 50%, frequentists interpret this as meaning that heads will come up 50 times out of 100 tosses, while Bayesianists see it as a claim of 50% confidence that the coin will show heads.

Terminology

Also, let’s find out what E and H are in the formula (1).

In formula (1), H stands for Hypothesis, meaning a hypothesis or “a claim that an event has occurred.”

In addition, E in formula (1) stands for Evidence, meaning “new information.”

Therefore, $P(H)$ is the confidence in the claim that an event has occurred, and $P(H|E)$ represents the updated confidence after receiving new information.

$P(H)$ and $P(H|E)$ are respectively called prior probability and posterior probability. If we think of the words “prior” and “posterior,” we can understand them as “confidence in my claim before and after observing evidence,” respectively.

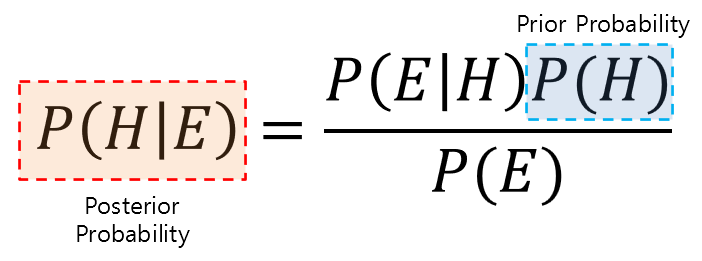
Figure 1. Bayes' theorem explains the relationship between prior and posterior probabilities.

Paradigm Shift in Probability Theory: From Deductive Reasoning to Inductive Reasoning

The reason why Bayes’ theorem is revolutionary is because it modified the fundamental paradigm of statistics.

Traditional statistics is based on the frequentist perspective, as explained earlier, and relies entirely on deductive reasoning. For example, it calculates the probability of an event occurring given the entire set of possible events, or assumes the statistical distribution of a population and tests the significance of differences.

In other words, traditional statistics adopts a paradigm that strictly defines a probability space or a distribution of a population (population or sample) and accepts the results derived from calculations based on it.

On the other hand, Bayesian statistics is based on empirical or uncertain values such as prior probabilities and updates them based on additional information.

This approach is an inductive reasoning method, and Bayesian probability/statistics embodies the philosophy that we can approach truth more closely by obtaining additional evidence.

This has brought about a significant change in the paradigm of probability theory.

Understanding Bayes’ Theorem through Problem Solving

Let’s try to better understand the concept of Bayes’ theorem as a method of updating the confidence in a claim that an event has occurred based on new information, by solving a simple example problem.

Example 1

The incidence rate of disease A is known to be 0.1%. The sensitivity (probability of testing positive given that the disease is present) of the test for the disease is 99%, and the specificity (probability of testing negative given that the disease is absent) is 98%.

If a person tests positive for the disease, what is the probability that they actually have the disease?

Solution

In order to effectively solve problems using Bayes’ theorem, it is important to define Hypothesis and Evidence accurately, as mentioned earlier.

For this problem, Hypothesis and Evidence can be defined as follows:

• Hypothesis: It is true, meaning the person actually has the disease.
• Evidence: It is tested positive, indicating a positive diagnosis for the disease.

Therefore, the prior probability of disease A, denoted as $P(H)$, is 0.001, since the incidence rate of the disease is 0.1%.

The given sensitivity and specificity in the problem correspond to True Positive and True Negative, respectively, with values of $P(E|H) = 0.99$ and $P(E^c|H^c) = 0.98$.

This can be visualized in Figure 2 below.

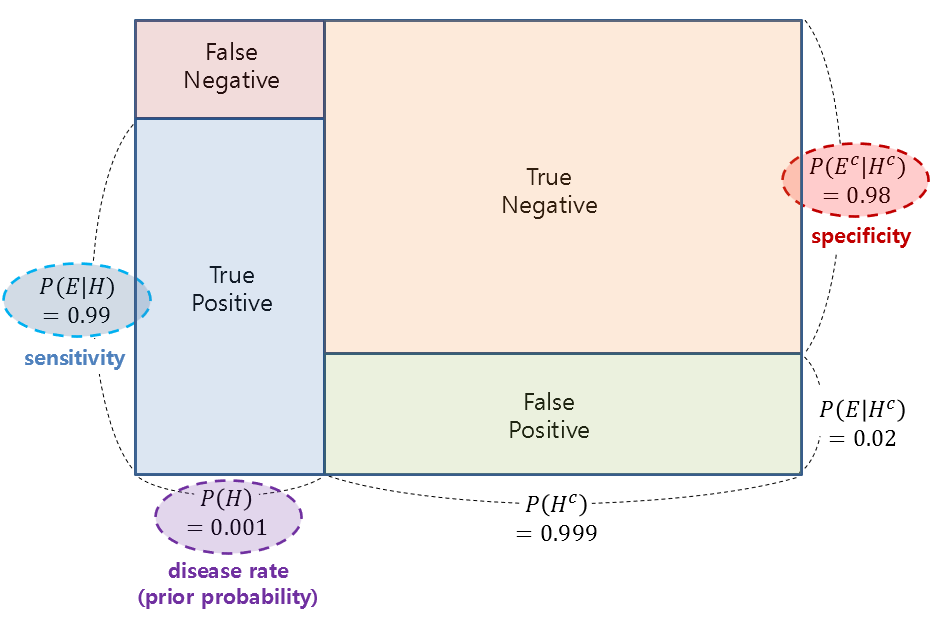
Figure 2. Visualization of the values of given probabilities as relative areas of rectangles

Rearranging Equation (1), we get the following Equation (2).

\[P(H|E) = \frac{P(E|H)P(H)}{P(E)} = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)}\]

Therefore, the desired probability $P(H|E)$ can be calculated as follows.

\[P(H|E) = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)} = \frac{0.001\times 0.99}{0.001\times 0.99 + 0.02\times 0.999}\notag\] \[= 0.047\text{ (rounded to three decimal places)}\]

Example 2

What is the probability that a person who has received a positive diagnosis twice in a row, as in Example 1, actually has the disease?

Solution

The reason for presenting a problem like Example 2 is that Bayes’ theorem is a way of updating the credibility, and in situations like Example 2, we can think of Hypothesis as follows:

• Hypothesis: The person has been diagnosed positive for the disease once, and this is true.

In other words, the posterior probability calculated as the result in Example 1 becomes the prior probability in Example 2, and we can calculate the updated posterior probability once again. Translation:

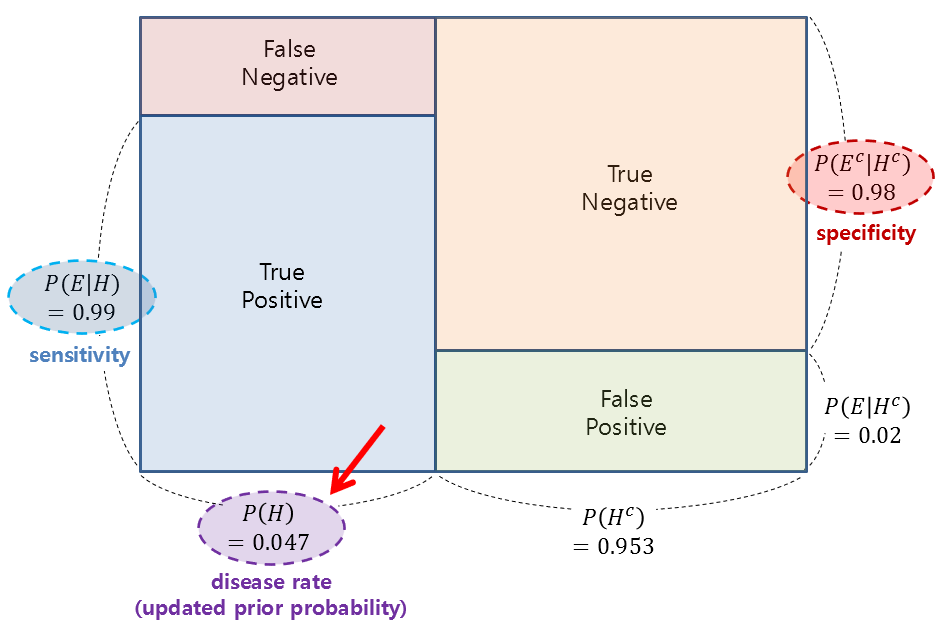
Figure 3. The posterior probability calculated in Example 1 is used as the prior probability in Example 2 (indicated by the red arrow), and it can be used to calculate the updated posterior probability once again. The figure visualizes the relative areas of the given probability values as rectangles.

Therefore, the value of $P(H|E)$ that we want to calculate is as follows.

\[P(H|E) = \frac{P(E|H)P(H)}{P(E|H)P(H)+P(E|H^c)P(H^c)} = \frac{0.047\times 0.99}{0.047\times 0.99 + 0.02\times 0.953}\notag\] \[= 0.709\text{ (rounded to three decimal places)}\]

In other words, based on the updated probability (i.e., the confidence in the fact that the person has the disease) obtained by further updating the prior probability calculated in Example 1,

we can say with about 70% confidence that the person may have the disease.