What is frequency resolution?

Frequency resolution refers to how closely spaced the values of a frequency band can be observed in the frequency domain when observing a desired signal. It can be thought of as a similar concept to obtaining a dense time signal when recording a signal with a high sampling frequency during time signal sampling.

Typically, when discussing frequency resolution, it is said that a longer length of the time window being observed results in better frequency resolution in the frequency domain (i.e., the ability to observe frequencies more closely), and a higher sampling rate results in denser observations in the time domain. This may initially seem somewhat ambiguous. Let’s explore this topic in more detail.

All Fourier analyses start from the Fourier series. When observing a function $f(t)$ with a period of $T$, the weights corresponding to each frequency value can be determined as follows:

\[a_k = \frac{1}{T}\int_{-\infty}^{\infty}f(t) exp(-j2\pi \frac{k}{T}t)dt\]

Therefore, when analyzing a periodic function, we can determine how closely spaced the frequencies can be observed in the frequency domain depending on the length of the period. This is because $a_k$ is drawn with an interval of $\frac{1}{T}$ (since the internal $k$ in the exponential term is an integer).

Figure 1 represents this fact well. At this point, it is important to note that the domain of the frequency domain is an integer $k$, but we know that $\frac{1}{T}$ can be expressed as $df$. Therefore, as can be seen in the Fourier series, the period of the signal in the time domain determines the value of $df$ in the frequency domain, which directly corresponds to the frequency resolution.

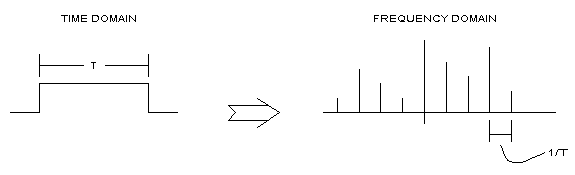
Figure 1. Length of time window and frequency resolution. Frequency resolution is expressed as (1/T).
Source: http://www.skylondaworks.com/sc_resol.htm

However, an important question may arise here. That is, the signals we obtain or analyze are not perfect periodic signals, but digital signals that are not continuous. Therefore, using only the Fourier series may not fully explain the frequency resolution of the Short Time Fourier Transform (STFT). Hence, let’s briefly understand the principles of the Discrete Fourier Transform (DFT) and delve into why the frequency resolution is determined by the window size in the STFT in more detail. Translation:

Principles of Discrete Fourier Transform

Discrete Fourier Transform (DFT) is a modification of the Discrete Time Fourier Transform (DTFT) that allows for the interpretation of non-periodic signals using computers or digital devices. The main reason why DTFT cannot be used directly in computers is that while time is discrete (hence the name “Discrete Time”), frequency is not. The formulas for DFT and DTFT are as follows:

\[X_{DFT}[k] = \sum_{n=0}^{N-1}x[n]\exp(-j2\pi \frac{k}{N}n)\quad(k \text{ is an integer})\] \[X_{DTFT}(f) = \sum_{n=-\infty}^{\infty}x[n]\exp(-j2\pi fn)\]

In other words, the formula for DFT is obtained by dividing the continuous frequency $f$ in DTFT into $N$ discrete frequency points. The value of $N$ in DFT corresponds to the N-point Fast Fourier Transform (NFFT) used in MATLAB. (FFT and DFT have algorithmic differences, but the principles are the same.)

To explain the working principle of DFT in a simplified way¹, it can be said that it involves multiplying the signal $x[n]$ of length T samples by a cosine function $\cos(2\pi\frac{1}{T}n)$ with a frequency of $1/T$. The result of this multiplication is denoted as $a_1$ and stored. Similarly, cosine functions with frequencies of $k/T$ where $k=1, 2, \cdots, N$ are prepared and multiplied with the original signal $x[n]$ to obtain the values $a_k$ where $k=1,2,\cdots,N$ and stored. The same process is performed for sine functions, and the output values are denoted as $b_n$.

Then, what do $a_k$ and $b_k$ represent? $a_k$ or $b_k$ indicates the similarity between the signal $x[n]$ and the cosine or sine signal with a frequency of $k/T$ ².

If we write $X[k] = a_k- jb_k$ with the imaginary unit $j$³, then ultimately this represents the same meaning as the DFT formula mentioned above:

\[X_{DFT}=\sum_{n=0}^{N-1}x[n]\exp\left(-j2\pi\frac{k}{N}n\right)\]

In other words, the DFT formula involves element-wise multiplication and summation of $x[n]$ and $\exp(-j2\pi\frac{k}{N}n)$⁴.

The reason why the length of the time window determines frequency resolution

Returning to our original problem, why does the length of the window in STFT affect frequency resolution?

This is because, in order to achieve the purpose of Short Time Fourier Transform, we must consider a window that is shorter than the entire length of the signal. Additionally, according to the principle of DFT, the frequencies that a computer can represent must be integer multiples of $1/T$, where $T$ is the length of the time window.