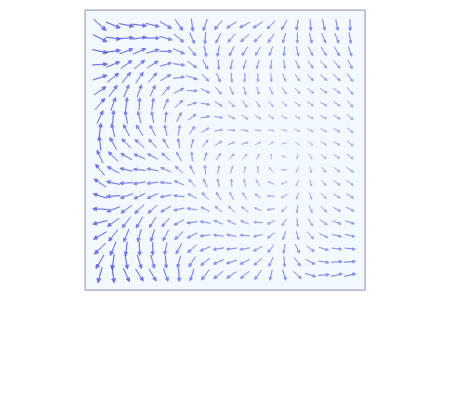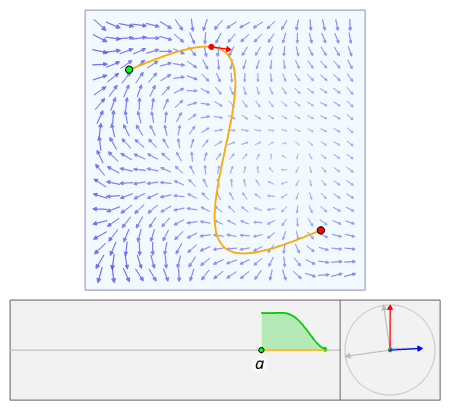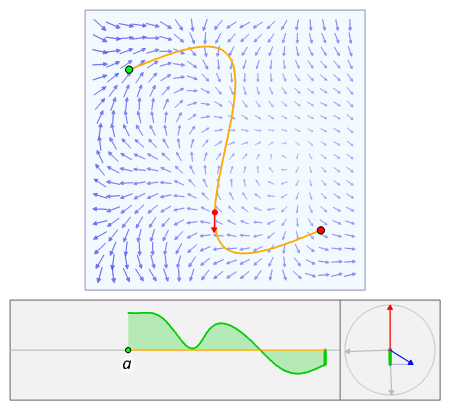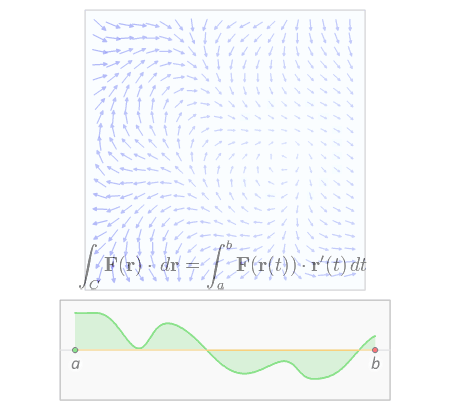
The line integral is a problem that calculates the work done along a given path for a given vector field.
Image source: Wikipedia, Line integral of a vector field
Work in Physics
The most useful concept to apply the concept of line integrals is “work” in physics.
In physics, work is defined as follows:
\[\text{work} = \text{force} \times \text{distance}\]Through Figure 1 below, we can express the work done by Charles in formula when he moves a distance of $s$ by a force $F$:
\[W=Fs\]
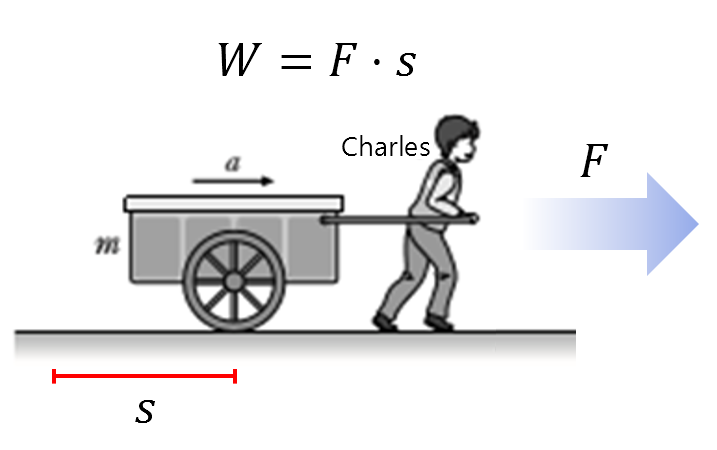
Figure 1. The work done by Charles as he pulls the cart is the product of force and displacement.
Image source: EBS
However, let’s say that when Charles pushes the cart, he doesn’t push it straight forward, but at an angle in the upward diagonal direction.
In this case, if we assume that the angle between the horizontal plane and the force vector ($\vec{F}$) is $\theta$, we can calculate the work done by taking the dot product with the direction vector related to the displacement as follows:
\[W=\vec{F}\cdot \vec{s}=|\vec{F}||\vec{S}|\cos\theta\]
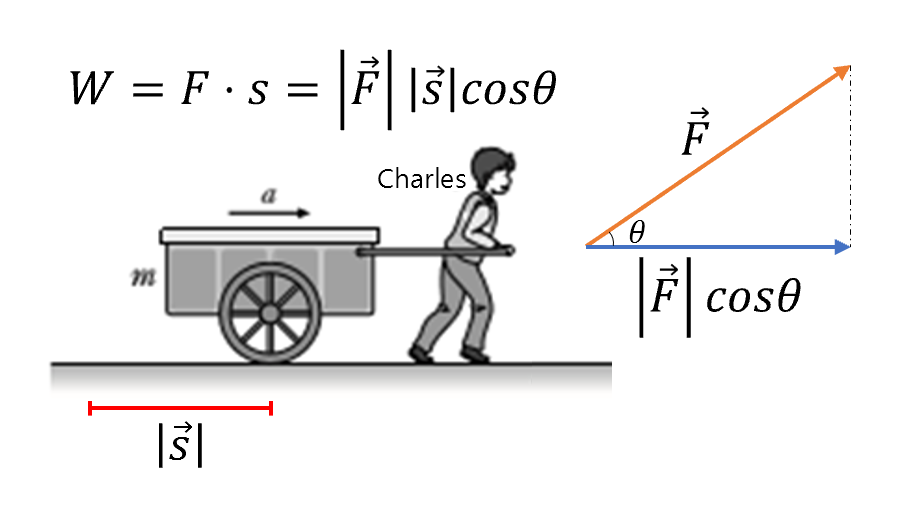
Figure 2. When pulling a cart aslant instead of straight, the work done by the person can be calculated by the dot product of vectors.
Image source: EBS
About more complex paths…
Let’s consider a scenario where the person, Chul-Soo, did different work three times during the entire distance he moved.
In other words, imagine that the magnitude of the force used or the angle at which the force was applied differed in each of the three sections of the entire distance, as shown in Figure 3 below.
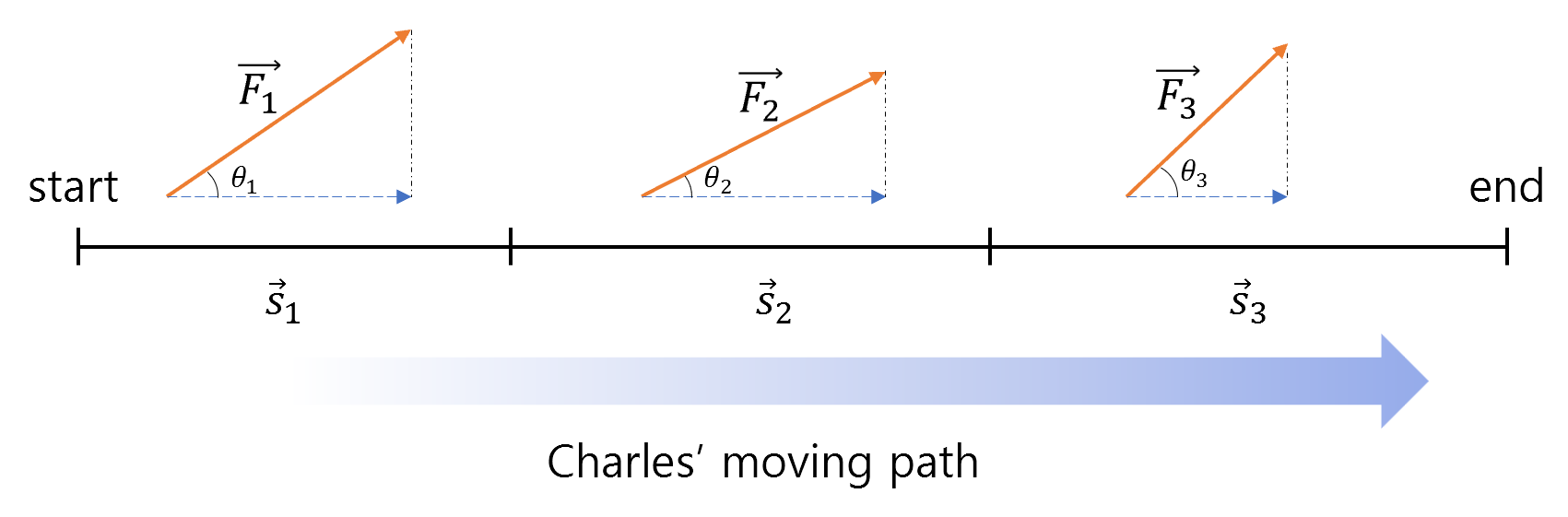
Figure 3. By adding the work done in each section after dividing the entire movement into three segments as shown in the figure, the total work done in the entire path can be obtained.
Then, the total work done by Chul-Soo in the entire path can be expressed as follows:
\[W = W_1 + W_2 + W_3 = \sum_{i=1}^{3}\vec{F}_i\cdot \vec{s}_i\]Now, let’s make the path a little more complicated.
Suppose we want to calculate the work done along the winding path shown as a black solid line in Figure 4 below. To do this, we can divide the path into straight segments as shown by the red dashed lines and add up the work done in each segment.
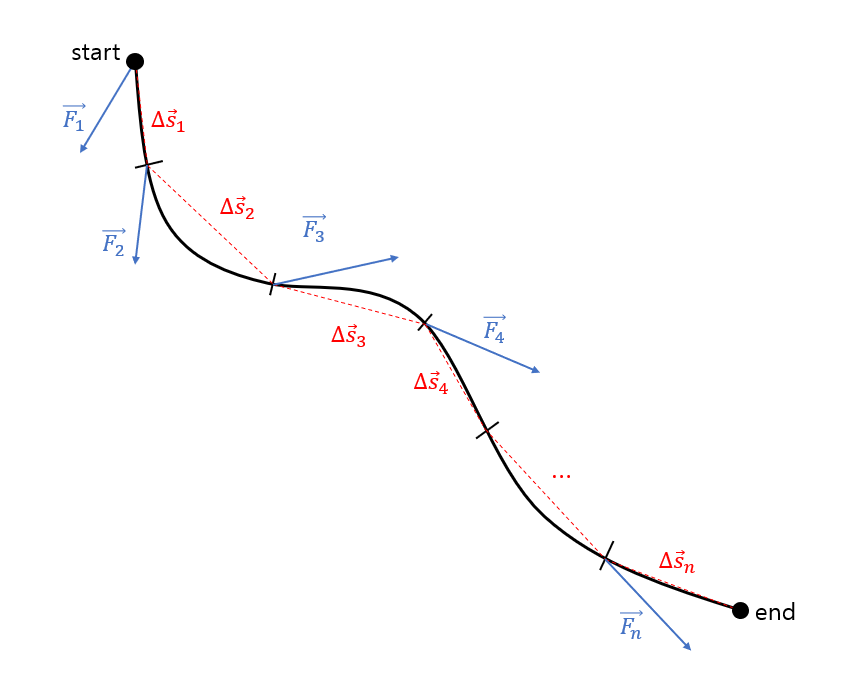
Figure 4. To calculate the work done on a more complex path, divide the path into segments and add up the work done in each segment.
The amount of work represented in Figure 4 can be expressed by the following formula:
\[W = W_1+W_2+\cdots +W_n = \sum_{i=1}^{n}\vec{F}_i\cdot \Delta \vec{s}_i\]When calculating the work as in equation (4), we can think of dividing the path into infinitely small segments as follows:
\[W = \lim_{|\Delta \vec{s}|\rightarrow 0}\sum_{i=1}^{n}\vec{F}_i\cdot \Delta \vec{s}_i\]We can define this value as a line integral:
\(\Rightarrow \int_C\vec{F}\cdot d\vec{s}\)
Line Integral
When expressing line integrals, the integrand $d\vec{s}$ used in equation (6) is often written as $d\vec{r}$.
\[\int_C\vec{F}\cdot d\vec{r}\]In actual problems, the vector $\vec{F}$ seen in Figure 4 is given as a vector field, which can generally be thought of as follows:
\[\vec{F(x,y)} = P(x,y)\hat{i} + Q(x,y)\hat{j}\]Here, $F(x,y)$ refers to a field rather than a force, and $P(x,y)$ and $Q(x,y)$ represent the $x$ and $y$ components, respectively, at all $(x,y)$ coordinates.
Additionally, the curve represented by the path of movement can be given as $y=f(x)$, $z=f(x,y)$, or as a parametric equation like:
\[\begin{bmatrix} x(t) = g(t) \\ y(t) = h(t) \end{bmatrix}\]Example Problem Solution
Given the vector field $F = xy\hat{i} -y^2\hat{j}$, find the amount of work done along the path below:
\[y=\frac{1}{2}x\text{ where } 0<x<2\]
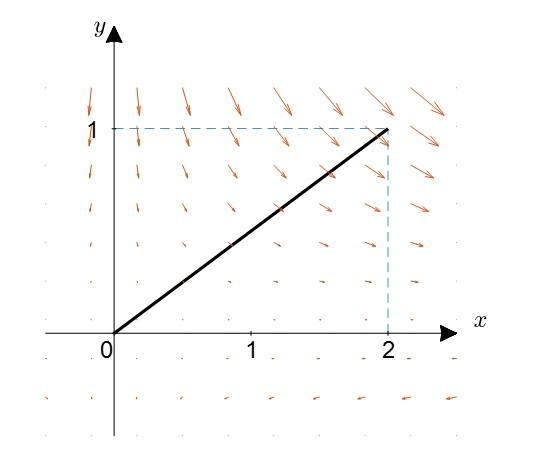
Figure 5. Vector field and path of movement in the example problem
The integral value we want to find is as follows:
\[\int_C\vec{F}\cdot d\vec{r}\]Here, $d\vec{r}$ can be expressed as the sum of the $x$ component $dx$ and the $y$ component $dy$, so we can think of it as follows:
\[d\vec{r} = \hat{i}dx+\hat{j}dy\]Therefore, when we take the dot product with the given vector field $\vec{F}$:
\[\vec{F}\cdot d\vec{r} = (xy\hat{i} - y^2\hat{j})\cdot (\hat{i}dx + \hat{j}dy) = xy(dx)-y^2(dy)\]Since the path is given as $y=(1/2)x$, we can substitute $y=(1/2)x$ into the above equation:
\[\vec{F}\cdot d\vec{r}\Rightarrow x\left(\frac{1}{2}x\right)dx-\left(\frac{1}{2}x\right)^2\left(\frac{1}{2}dx\right) =\left(\frac{1}{2}x^2-\frac{1}{8}x^2\right)dx\]Therefore, the line integral value is:
\[\int_{0}^{2}\left(\frac{1}{2}x^2-\frac{1}{8}x^2\right)dx=\int_{0}^{2}\left(\frac{3}{8}x^2\right)dx=\left[\frac{1}{8}x^3\right]_{0}^{2} = 1\]