Phase planes that correspond to dots on Trace-Determinant plane
Source: MIT Mathlets,
https://mathlets.org/mathlets/linear-phase-portraits-matrix-entry/
Prerequisites
To understand this content well, it is recommended that you know the following:
Review of Phase Plane
In Phase Plane, it was shown that a linear system of differential equations can be expressed using a matrix as follows:
\[\begin{bmatrix}dx/dt \\ dy/dt\end{bmatrix} = \begin{bmatrix}a & b \\ c & d \end{bmatrix}\begin{bmatrix}x \\ y \end{bmatrix} % Equation (1)\]Then, the eigenvalues and eigenvectors were calculated from the matrix of the above equation, and the changes in the shape of the phase plane according to the values of the eigenvalues and eigenvectors were investigated.
As confirmed, when all eigenvalues are real, the eigenvectors acted as the new axes of change.
If the eigenvalues are positive, the function values along the corresponding eigenvectors move away from the origin as time passes.
Also, if the eigenvalues are negative, the function values move towards the origin along the corresponding eigenvectors as time passes.
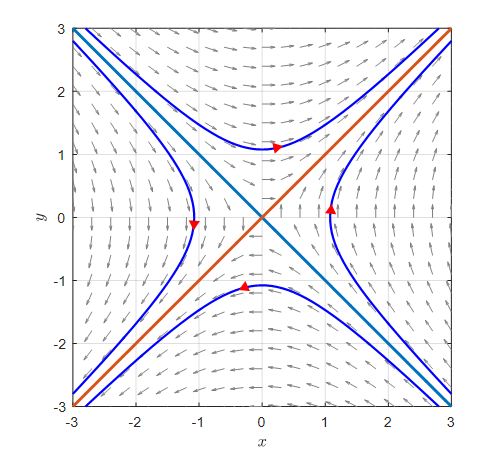
Figure 1. Case of real eigenvalues. Function values move away from the origin along the eigenvectors corresponding to positive eigenvalues, and towards the origin along the eigenvectors corresponding to negative eigenvalues.
On the other hand, if the eigenvalues are complex, the phase plane takes a shape that seems to rotate around the origin.
In this case, if the real part of the complex eigenvalue is negative, the function values converge towards the origin.
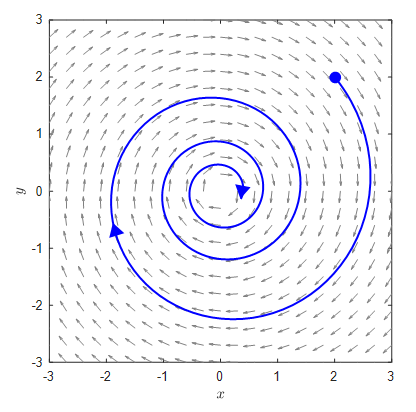
Figure 2. Case of complex eigenvalues. Function values rotate towards the origin and converge towards it when the real part of the complex eigenvalue is less than 1.
Meanwhile, it was found that when the eigenvalue is a complex number and the real part is positive, the phase plane takes the form of rotating away from the origin.
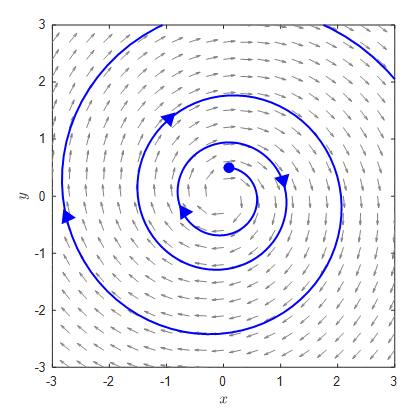
Figure 3. The case of complex eigenvalues. If the real part of the complex eigenvalue is greater than 1, it rotates away from the origin.
Also, there are cases where the eigenvalues overlap. This is called the case of having repeated eigenvalues. In the case of having repeated eigenvalues, there are also cases where the eigenvectors cannot be distinguished.
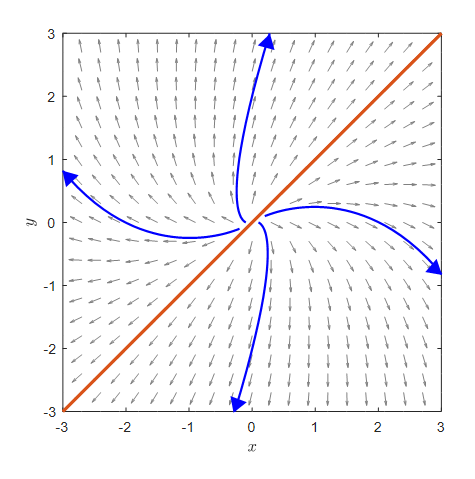
Figure 4. The case of having repeated eigenvalues. In the case of having repeated eigenvalues, many eigenvectors overlap.
Characteristic equation
As seen above, to analyze the form of the phase plane, we need to analyze the eigenvalues.
The method for calculating the eigenvalues is to analyze the characteristic equation of the matrix.
From the definitions of eigenvalues and eigenvectors, we can obtain the characteristic equation as follows.
For any matrix $A$ and eigenvalue $\lambda$, eigenvector $v$, the following must hold.
\[A\vec{v} = \lambda \vec{v} % Equation (2)\]The right-hand side of the above equation can also be written as follows.
\[\lambda \vec{v} = \lambda \vec{v} I % Equation (3)\]Here, $I$ is the identity matrix.
In other words, the equation for eigenvalues and eigenvectors can also be written as the following equation by rearranging it.
\[A\vec{v} - \lambda \vec{v} I = 0 % 식 (4)\] \[\Rightarrow (A-\lambda I)\vec{v} = 0 % 식 (5)\]If matrix $A$ is a $2 \times 2$ matrix as follows,
\[A = \begin{bmatrix}a & b \\c & d\end{bmatrix} % Equation (6)\]Equation (5) will change as follows.
\[\text{Equation (5)}\Rightarrow \begin{bmatrix}a-\lambda & b \\ c & d-\lambda\end{bmatrix}\vec{v} = 0 % Equation (7)\]Here, if $\vec{v}$ is a zero vector, there is no reason to find the eigenvector, resulting in a trivial solution. Therefore, to obtain a meaningful solution rather than a trivial solution, the matrix on the left-hand side of Equation (7) must not have an inverse matrix.
Thus, we can say that the eigenvector $\vec{v}$ is not a trivial solution when the following conditions are satisfied.
\[\det\left(\begin{bmatrix}a-\lambda & b \\ c & d-\lambda\end{bmatrix}\right) = 0 % Equation (8)\]According to the definition of the determinant, if we solve this equation a little more,
\[\Rightarrow (a-\lambda)(d-\lambda)-bc = 0 % Equation (9)\] \[\Rightarrow \lambda ^2 - (a+d)\lambda + ad-bc = 0 % Equation (10)\]and so on. This equation is called the characteristic equation.
If we find the solution to this characteristic equation, we can obtain the eigenvalues.
Trace & Determinant
$a+d$ represents the trace of the original Equation (6) matrix $A$, and $ad-bc$ represents the determinant of the Equation (6) matrix $A$.
Substituting $T$ for $a+d$ and $D$ for $ad-bc$, and applying the formula to Equation (10), we can calculate the eigenvalues, which are the solutions of the characteristic equation.
\[\lambda_{1, 2} = \frac{T\pm\sqrt{T^2-4D}}{2} % Equation (11)\]When reviewing the phase plane earlier, how did we distinguish the eigenvalues?
We distinguished between two eigenvalues that were both real, complex, or had double roots.
Therefore, we can determine whether the two eigenvalues are real, complex, or have double roots by checking the sign of $T^2-4D$ inside the square root in Equation (11).
In other words,
- If $T^2-4D > 0$, both eigenvalues are real.
- If $T^2-4D < 0$, both eigenvalues are complex.
- If $T^2-4D = 0$, there is a repeated eigenvalue.
Trace-Determinant Plane
We can take one step further and consider a plane with trace and determinant values as variables.
For example, if we think of a plane where the $x$-axis represents the trace value and the $y$-axis represents the determinant value, we can determine whether the eigenvalues are real, complex, or repeated based on the curve $D=\frac{1}{4}T^2$.
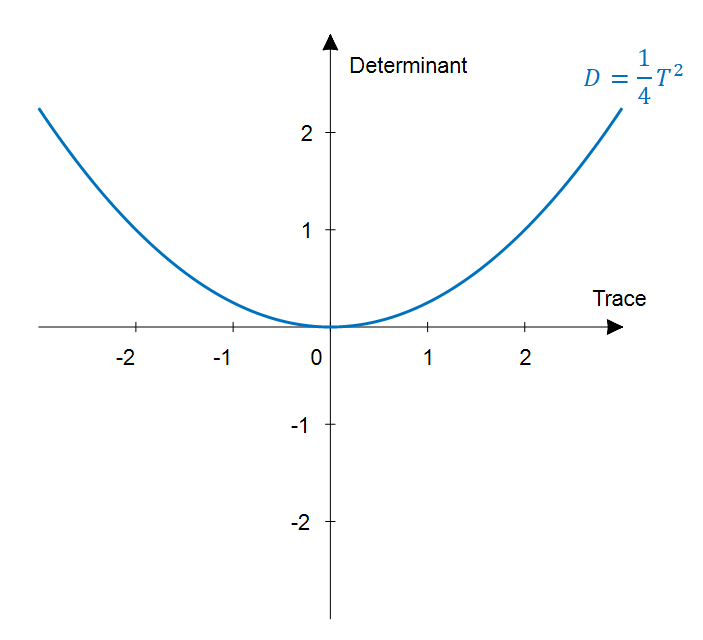
Figure 5. The curve corresponding to the condition $D=1/4 T^2$
In other words, given a system of coupled differential equations as in equation (1), we calculate the values of the trace (T) and determinant (D) of the matrix, check the (T,D) value on the Trace-Determinant plane, and compare its position with the curve shown in Figure 5.
If (T,D) is above the curve, both eigenvalues are complex.
(If we think about it carefully, the condition $T^2-4D < 0$ is equivalent to $D > \frac{1}{4}T^2$.)
If (T,D) is below the curve, both eigenvalues are real.
Finally, if (T,D) is on the curve, there is a repeated eigenvalue.
We can check these results using the applet at the top of this article.
Case with complex eigenvalues
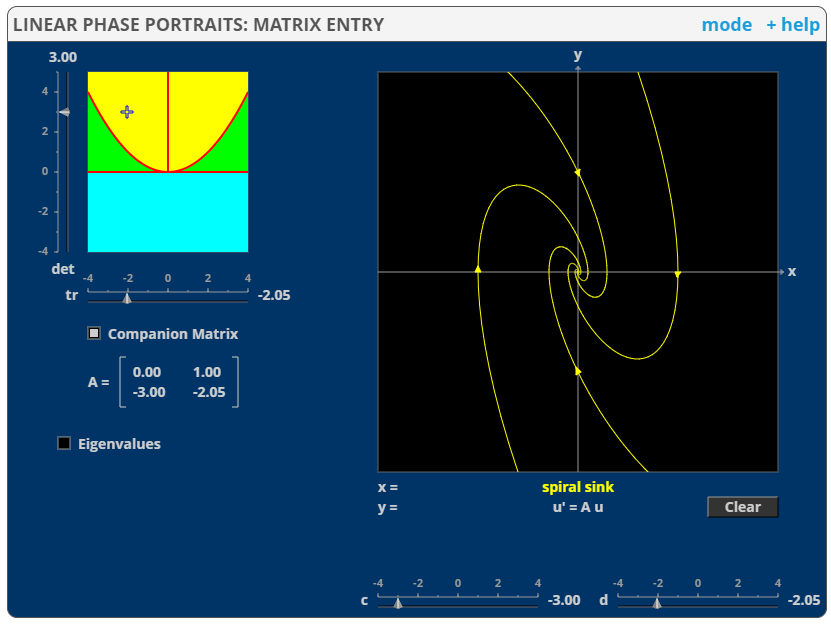
Figure 6. Coordinates and phase plane on the Trace-Determinant plane when the eigenvalues are complex.
Case with real eigenvalues
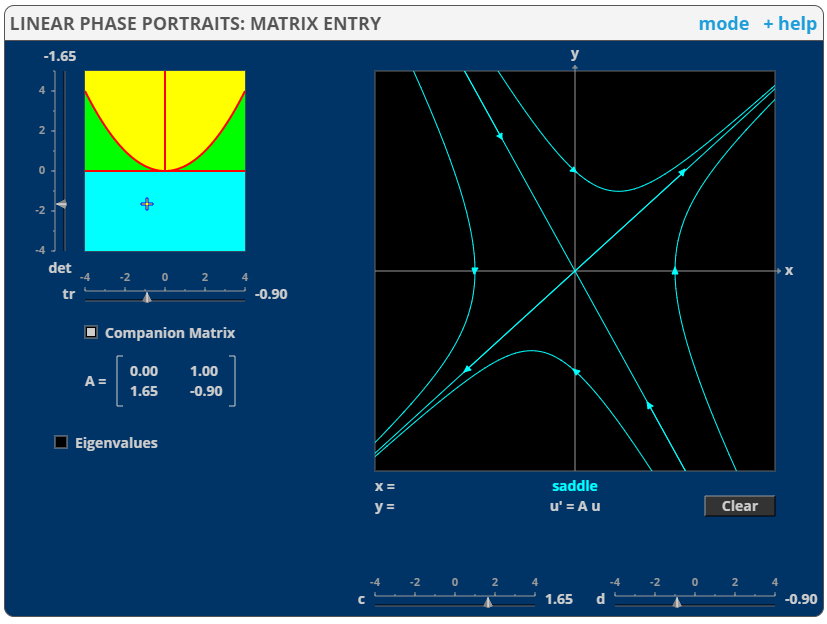
Figure 7. Coordinates and phase plane on the Trace-Determinant plane when the eigenvalues are real.
Case with repeated eigenvalues
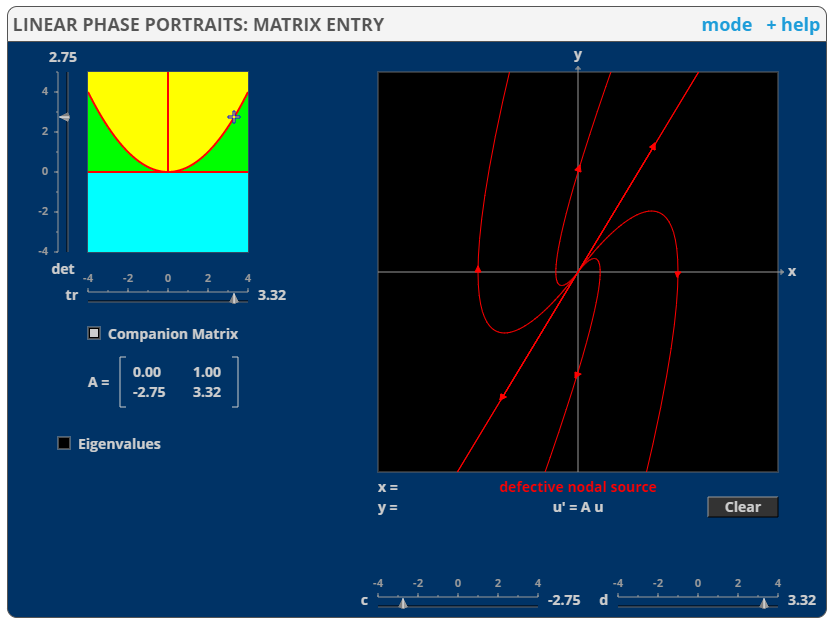
Figure 8. Coordinates and phase plane on the Trace-Determinant plane when there is a repeated eigenvalue.