이 문서의 한국어 버전은 아래의 위치에서 찾을 수 있습니다. (You can find a Korean version of this article as below.)

• 허수의 존재 의미에 대하여

1. Discovering numbers

Before we delve into the concept of complex numbers, we need to consider the system of numbers. Generally, the system of numbers is known as follows.

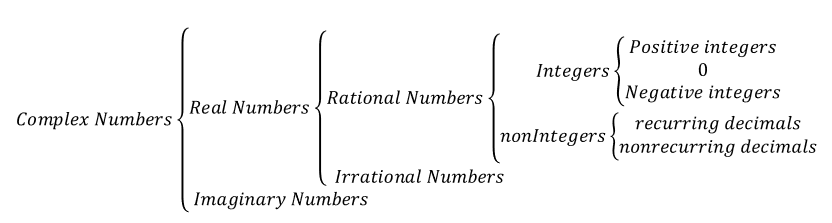
The above diagram divides complex numbers into real and imaginary numbers and divides real numbers into rational and irrational numbers. This is a top-down approach to describing the number system, but originally, the number system would have started from the discovery of natural numbers. In other words, the first discovered number system would have been natural numbers (positive integers).

So, for example, someone would have discovered that two cows and two dogs are the same as four animals. This would have been used as a security measure to protect property.

After the discovery of natural numbers, the concept of positive rational numbers might have been discovered. Someone would have found an answer to the question, “If there are 1 and 2 animals, then there are no 1.5 animals, right?” However, it is a well-known fact that the concept of rational numbers is now very useful.

Through the repeated process of discovering number systems, the concept of negative numbers might have been discovered. The concept of negative numbers might have been difficult and considered useless at first because it extended the system of numbers to include invisible numbers from the perspective of positive integers. However, everyone living in the present era is likely to realize, even without any special explanation, how useful the concept of negative numbers is.

2. Expansion of meaning of multiplication

Multiplication is often understood as repeated addition, but the introduction of negative numbers expands the original meaning of multiplication to include a notion of direction. Moreover, the concept of squaring can be seen as a repetition of the multiplication pattern.

The system of negative numbers expands the meaning of multiplication by introducing the idea of transforming numbers in a certain direction. Multiplication is an operation that expresses how much we want to increase a number in a certain direction starting from 1. For instance, $1\times3$ means that we want to increase the number 1 by a factor of 3 in the positive direction. Therefore, the positive direction is contrasted with the negative direction. Consequently, $-3$ can be thought of as $1\times (-1) \times 3$, which means that we want to increase the number 1 by a factor of 3 in the negative direction (-1). By comparing $1\times 3$ and $1\times (-1)\times 3$, we can see that the concept of direction (-1) that was previously absent is now being expressed.

Thus, the discovery of the system of negative numbers expands the range of transformation of multiplication from a unidirectional to a bidirectional transformation. The continual use of the term “direction” may lead some readers to wonder what it means. Essentially, the concept of numbers can now be extended to the concept of vectors. The discovery of negative numbers expands the concept of scalar, which was previously defined in only one direction, to a one-dimensional vector.

3. Discovering imaginary numbers

The number system that’s beyond the dimension of real numbers. Imaginary numbers mean rotation.

People may have needed to introduce the concept of imaginary numbers to answer the question, “Does x exist when x^2=-9?”. This may seem like a foolish question, but we can extend the concept of numbers and find the answer if we consider that x^2=-1 has a solution in the form of an imaginary number.

What does the discovery of imaginary numbers have to do with extending the one-dimensional vector space that the number system has been expressed in thus far? The discovery of imaginary numbers has a remarkable significance in that it expands the number system, which was previously represented as a one-dimensional vector in the real number field, to a two-dimensional vector¹.

To understand the concept of imaginary numbers precisely, we need to think again about the meaning of squaring a number. What is squaring? It means multiplying the same number twice. That is, $x^2$ means $x$ multiplied by itself. For example, $3^2$ has the following meaning: $1$ times $3$ times $3$. That is, it means making the original number, $1$, three times as large in the positive direction and then making it three times as large again in the positive direction.

Now, let’s consider the square of a negative number. What about $(-3)^2$? It will have the meaning of 1 times -1 times 3 times -1 times 3. That is, it means making the number 1 three times as large in the negative direction and then making it three times as large again in the opposite direction. As a result, we can think of $x=3$ or $x=-3$ when $x^2=9$.

When we consider $1$ times $x$ times $x = -9$, we must be able to get $-9$ when we perform the transformation of multiplying the same number twice. We cannot solve this equation with a real number because multiplying a positive number twice results in a positive number, and multiplying a negative number twice results in a positive number.

If we assume that the number system has additional dimensions beyond the real number line, a one-dimensional vector with direction can be rotated +90 degrees and then another +90 degrees, resulting in -1. In other words, it is not necessary to only consider the multiplication operation as having meaning in terms of the front and back directions on a one-dimensional line. Just as the real number system can be represented on a single axis, the concept of imaginary numbers can be represented on a new axis orthogonal to the real number axis.

Therefore, the discovery of the concept of a new dimension in the form of imaginary numbers reveals the fact that numbers are not one-dimensional. That is, if the imaginary unit $i$ represents a 90-degree counterclockwise rotation into the imaginary dimension, then in the one-dimensional real number space, it follows that $i^2=-1$.² If we only consider the one-dimensional space, it may seem like a very strange phenomenon, like how we in three-dimensional space cannot understand the world in four dimensions.